Area of a triangle: Difference between revisions

Revision as of 16:26, 2 November 2007

The area of any triangle can be calculated using the following equation:

$Area=\left({\frac {1}{2}}\right)bc(sinA)=\left({\frac {1}{2}}\right)ac(sinB)=\left({\frac {1}{2}}\right)ab(sinC)$

Triangle

For right triangles, the angle C, opposite the hypotenuse (c), is 90 degrees. The sine of 90 degrees is 1, so the equation reduces to:

$Area=\left({\frac {1}{2}}\right)ab$

@@ Line 1: / Line 1: @@
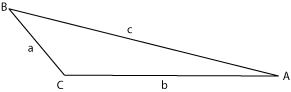
-The area of any triangle can be calculated using the following equation:
+The area of any [[triangle]] can be calculated using the following equation:
 <math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math>
@@ Line 9: / Line 9: @@
 == Right triangles ==
-For right triangles, the angle C, opposite the hypotenus (c), is 90 degrees.  The sign of 90 degrees is 1, so the equation reduces to:
+For [[right triangle|right triangles]], the angle C, opposite the [[hypotenuse]] (c), is 90 degrees.  The sine of 90 degrees is 1, so the equation reduces to: