User talk:Paul Wormer/scratchbook1: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>Paul Wormer
No edit summary
imported>Paul Wormer
No edit summary
 
(8 intermediate revisions by the same user not shown)
Line 1: Line 1:
{{Image|Param1 plane.png|right|350px|<small>Equation for plane. ''X'' is arbitary point in plane; <font style<nowiki>=</nowiki> "vertical-align: text-top;"> <math>\scriptstyle\vec{\mathbf{a}}</math></font> and <font style<nowiki>=</nowiki> "vertical-align: text-top;"> <math>\scriptstyle\hat{\mathbf{n}} </math></font> are collinear.</small>}}
==Parabolic mirror==
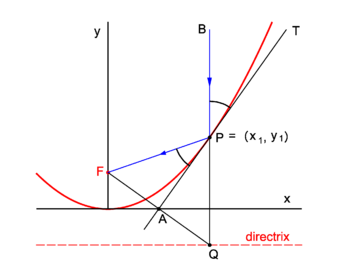
In [[analytic geometry]] several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. One such equation is illustrated in the figure. Point ''X'' is an arbitrary point in the plane and ''O'' (the origin) is outside the plane. The point ''A'' in the plane is chosen such that vector
{{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}}
:<math>
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
\vec{a} \equiv  \overrightarrow{OA}
 
</math>
Consider in figure  2 the arbitrary  vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law:  incidence angle is angle of reflection.  The angles involved are with the line  ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''.  
is  orthogonal to the plane. The collinear vector
:<math>
\vec{n} \equiv \frac{\vec{a}}{a} \quad \hbox{with}\quad a \equiv {|\vec{a}|}
</math>
is a unit (length 1) vector  normal (perpendicular) to the plane. Evidently ''a'' is the distance of ''O'' to the plane. The following relation holds for an arbitrary point ''X'' in the plane
:<math>
\left(\vec{r}-\vec{a}\right)\cdot \vec{n} = 0 \quad\hbox{with}\quad \vec{r} \equiv\overrightarrow{OX}\quad\hbox{and}\quad  \vec{r}-\vec{a} = \overrightarrow{AX} .
</math>


This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in ''O''. Dropping arrows for component vectors (real triplets) that are written bold, we find
Clearly &ang;''BPT'' = &ang;''QPA'' (they are vertically opposite angles). Further &ang;''APQ'' = &ang;''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence &ang;''FPA'' = &ang;''BPT''.
:<math>
\mathbf{r}\cdot \mathbf{n} = \mathbf{a}\cdot \mathbf{n}
\Longleftrightarrow
x u +y v+z w =  a
</math>
with
:<math>
\mathbf{a} = (u,\;v,\; w), \quad
\mathbf{r} = (x,\;y,\; z), \quad\hbox{and}\quad \mathbf{a}\cdot \mathbf{n} =
\mathbf{a}\cdot \frac{\mathbf{a}}{a} = a  = \sqrt{u^2+v^2+w^2}.
</math>


Conversely, given the following equation for a plane
We prove the congruence of the triangles: By the definition of  the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus.  The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, &minus;''f''). The line segment ''FQ'' has the equation
:<math>
:<math>
ax+by+cz = d \,
\lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1.
</math>
</math>
it is easy to derive the same equation.
The midpoint ''A''  of ''FQ'' has coordinates (&lambda; = &frac12;):
Write
:<math>
:<math>
\mathbf{r} = (x,\;y,\; z), \quad\mathbf{f} = (a,\;b,\; c), \quad\hbox{and}\quad
\frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} =
\mathbf{a} \equiv \frac{d}{\mathbf{f}\cdot\mathbf{f}} \mathbf{f}.
\begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}.
</math>
</math>
It follows that
Hence ''A'' lies on the ''x''-axis.
The parabola has equation,
:<math>
:<math>
\mathbf{f}\cdot\mathbf{r} = d= \mathbf{f}\cdot \mathbf{a}.
y = \frac{1}{4f} x^2.
</math>
</math>
Hence we find the same equation,
The equation of the tangent at ''P'' is
:<math>
:<math>
\mathbf{f}\cdot(\mathbf{r}-\mathbf{a}) = 0 \;\Longrightarrow\; \mathbf{n}\cdot(\mathbf{r}-\mathbf{a}) = 0 \quad\hbox{with}\quad \mathbf{n} = \frac{\mathbf{f}}{\sqrt{a^2+b^2+c^2}}
y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}.
</math>
</math>
where '''f''' , '''a''', and '''n''' are collinear. The equation may also be written in the following mnemonically convenient form
This line intersects the ''x''-axis at ''y'' = 0,
:<math>
:<math>
\mathbf{a}\cdot(\mathbf{r}-\mathbf{a}) = 0,
0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x
\Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1.
</math>
</math>
which is the equation for a plane through a point ''A'' perpendicular to <font style="vertical-align: top;"><math>\overrightarrow{OA}</math></font>.
The intersection of the tangent with the ''x''-axis is the point ''A'' = (&frac12;''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA''  are of equal length and hence the triangles are congruent.

Latest revision as of 23:40, 3 April 2010

Parabolic mirror

PD Image
Fig. 2. Reflection in a parabolic mirror

Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.

Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.

Clearly ∠BPT = ∠QPA (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA = ∠BPT.

We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation

The midpoint A of FQ has coordinates (λ = ½):

Hence A lies on the x-axis. The parabola has equation,

The equation of the tangent at P is

This line intersects the x-axis at y = 0,

The intersection of the tangent with the x-axis is the point A = (½x1, 0) that lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.

Retrieved from "https://citizendium.org/wiki/index.php?title=User_talk:Paul_Wormer/scratchbook1&oldid=612762"