User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 66: | Line 66: | ||
\vec{u} = \overrightarrow{AB}= \vec{b}-\vec{a} ,\quad \vec{v} = \overrightarrow{AC}= \vec{c}-\vec{a}. | \vec{u} = \overrightarrow{AB}= \vec{b}-\vec{a} ,\quad \vec{v} = \overrightarrow{AC}= \vec{c}-\vec{a}. | ||
</math> | </math> | ||
Because a plane is a 2-dimensional [[linear space]] and two non-collinear vectors in | Because a plane (an [[affine space]]), with a given fixed point as origin is a 2-dimensional [[linear space]] and two non-collinear vectors with "tails" in the origin are [[linearly independent]], it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors (this is also expressed as: any vector in the plane can be decomposed into components along the two non-collinear vectors). In particular, taking ''A'' as origin in the plane, | ||
:<math> | :<math> | ||
\overrightarrow{AP}= \vec{r}-\vec{a} = \lambda \vec{u} + \mu\vec{v},\qquad \lambda,\mu \in \mathbb{R}. | \overrightarrow{AP}= \vec{r}-\vec{a} = \lambda \vec{u} + \mu\vec{v},\qquad \lambda,\mu \in \mathbb{R}. | ||
| Line 84: | Line 84: | ||
\vec{r} = (1-\lambda-\mu)\, \vec{a}+ \lambda\, \vec{b} + \mu\,\vec{c} \;\equiv\; \xi_1\, \vec{a} +\xi_2\,\vec{b} + \xi_3\, \vec{c}\; , | \vec{r} = (1-\lambda-\mu)\, \vec{a}+ \lambda\, \vec{b} + \mu\,\vec{c} \;\equiv\; \xi_1\, \vec{a} +\xi_2\,\vec{b} + \xi_3\, \vec{c}\; , | ||
</math> | </math> | ||
we find that the real triplet (ξ<sub>1</sub>, ξ<sub>2</sub>, ξ<sub>3</sub>) with ξ<sub>1</sub> + ξ<sub>1</sub> + ξ<sub>1</sub> = 1 forms a set of coordinates for ''P''. The numbers {ξ<sub>1</sub>, ξ<sub>2</sub>, ξ<sub>3</sub> | ξ<sub>1</sub>+ ξ<sub>2</sub>+ ξ<sub>3</sub> = 1 } are known as the ''barycentric coordinates'' of ''P''. It is trivial to go from barycentric coordinates to the "three-point representation", | we find that the real triplet (ξ<sub>1</sub>, ξ<sub>2</sub>, ξ<sub>3</sub>) with ξ<sub>1</sub> + ξ<sub>1</sub> + ξ<sub>1</sub> = 1 forms a set of coordinates for ''P''. The numbers {ξ<sub>1</sub>, ξ<sub>2</sub>, ξ<sub>3</sub> | ξ<sub>1</sub>+ ξ<sub>2</sub>+ ξ<sub>3</sub> = 1 } are known as the ''[[barycentric coordinates]]'' of ''P''. It is trivial to go from barycentric coordinates to the "three-point representation", | ||
:<math> | :<math> | ||
\vec{r} = \xi_1 \vec{a} + \xi_2\vec{b} + \xi_3 \vec{c}\quad\hbox{with}\quad \xi_1 = 1- \xi_2-\xi_3 | \vec{r} = \xi_1 \vec{a} + \xi_2\vec{b} + \xi_3 \vec{c}\quad\hbox{with}\quad \xi_1 = 1- \xi_2-\xi_3 | ||
Revision as of 03:10, 1 April 2010
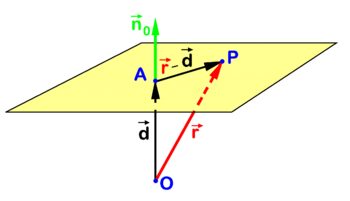
Point-normal representation
In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. One such equation is illustrated in figure 1. Point P is an arbitrary point in the plane and O (the origin) is outside the plane. The point A in the plane is chosen such that vector
is orthogonal to the plane. The collinear vector
is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane
This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find
with
and
Conversely, given the following equation for a plane
it is easy to derive the same equation. Write
It follows that
Hence we find the same equation,
where f , d, and n0 are collinear. The equation may also be written in the following mnemonically convenient form
which is the equation for a plane through a point A perpendicular to .
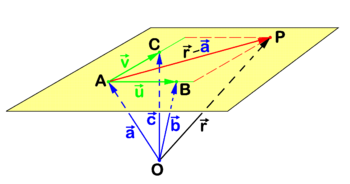
Three-point representation
Figure 2 shows a plane that by definition passes through non-coinciding points A, B, and C that moreover are not on one line. The point P is an arbitrary point in the plane and the reference point O is outside the plane. Referring to figure 2 we introduce the following definitions
Clearly the following two non-collinear vectors belong to the plane
Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors (this is also expressed as: any vector in the plane can be decomposed into components along the two non-collinear vectors). In particular, taking A as origin in the plane,
The real numbers λ and μ specify the direction of . Hence the following equation for the position vector of the arbitrary point P in the plane:
is known as the point-direction representation of the plane. This representation is equal to the three-point representation
where , , and are the position vectors of the three points that define the plane.
Writing for the position vector of the arbitrary point P in the plane
we find that the real triplet (ξ1, ξ2, ξ3) with ξ1 + ξ1 + ξ1 = 1 forms a set of coordinates for P. The numbers {ξ1, ξ2, ξ3 | ξ1+ ξ2+ ξ3 = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation",