User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
==Algebraic equations== | |||
In [[analytic geometry]] several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed. | |||
===Point-normal representation=== | ===Point-normal representation=== | ||
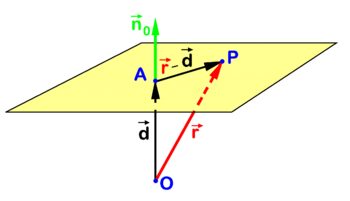
{{Image|Param1 plane.png|right|350px|<small>Fig. 1. Equation for plane. ''P'' is arbitary point in plane; <font style<nowiki>=</nowiki> "vertical-align: top;"> <math>\scriptstyle\vec{d}</math></font> and <font style<nowiki>=</nowiki> "vertical-align: text-top;"> <math>\scriptstyle \vec{n}_0 </math></font> are collinear.</small>}} | {{Image|Param1 plane.png|right|350px|<small>Fig. 1. Equation for plane. ''P'' is arbitary point in plane; <font style<nowiki>=</nowiki> "vertical-align: top;"> <math>\scriptstyle\vec{d}</math></font> and <font style<nowiki>=</nowiki> "vertical-align: text-top;"> <math>\scriptstyle \vec{n}_0 </math></font> are collinear.</small>}} | ||
One such equation is illustrated in figure 1. Point ''P'' is an arbitrary point in the plane and ''O'' (the origin) is drawn outside the plane, but may also be in the plane. The point ''A'' in the plane is chosen such that vector | |||
:<math> | :<math> | ||
\vec{d} \equiv \overrightarrow{OA} | \vec{d} \equiv \overrightarrow{OA} | ||
| Line 54: | Line 56: | ||
\mathbf{d}\cdot(\mathbf{r}-\mathbf{d}) = 0, | \mathbf{d}\cdot(\mathbf{r}-\mathbf{d}) = 0, | ||
</math> | </math> | ||
which is the equation for a plane through a point ''A'' perpendicular to <font style="vertical-align: | which is the equation for a plane through a point ''A'' perpendicular to <font style="vertical-align: top;"><math>\overrightarrow{OA}=\vec{d}</math></font>. | ||
===Three-point representation=== | ===Three-point representation=== | ||
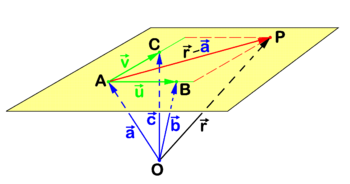
{{Image|Param2 plane.png|right|350px|<small> Fig. 2. Plane through points ''A'', ''B'', and ''C''.</small>}} | {{Image|Param2 plane.png|right|350px|<small> Fig. 2. Plane through points ''A'', ''B'', and ''C''.</small>}} | ||
Figure 2 shows a plane that by definition passes through non-coinciding points ''A'', ''B'', and ''C'' that moreover are not on one line. The point ''P'' is an arbitrary point in the plane and the reference point ''O'' is outside the plane. Referring to figure 2 we introduce the following definitions | Figure 2 shows a plane that by definition passes through non-coinciding points ''A'', ''B'', and ''C'' that moreover are not on one line. The point ''P'' is an arbitrary point in the plane and the reference point ''O'' is again drawn outside the plane, but the case that the plane passes through ''O'' is not excluded. Referring to figure 2 we introduce the following definitions | ||
:<math> | :<math> | ||
\vec{a} = \overrightarrow{OA},\quad \vec{b} = \overrightarrow{OB},\quad\vec{c} = \overrightarrow{OC},\quad \vec{r} = \overrightarrow{OP}. | \vec{a} = \overrightarrow{OA},\quad \vec{b} = \overrightarrow{OB},\quad\vec{c} = \overrightarrow{OC},\quad \vec{r} = \overrightarrow{OP}. | ||
Revision as of 04:40, 1 April 2010
Algebraic equations
In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed.
Point-normal representation
One such equation is illustrated in figure 1. Point P is an arbitrary point in the plane and O (the origin) is drawn outside the plane, but may also be in the plane. The point A in the plane is chosen such that vector
is orthogonal to the plane. The collinear vector
is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane
This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find
with
and
Conversely, given the following equation for a plane
it is easy to derive the same equation. Write
It follows that
Hence we find the same equation,
where f , d, and n0 are collinear. The equation may also be written in the following mnemonically convenient form
which is the equation for a plane through a point A perpendicular to .
Three-point representation
Figure 2 shows a plane that by definition passes through non-coinciding points A, B, and C that moreover are not on one line. The point P is an arbitrary point in the plane and the reference point O is again drawn outside the plane, but the case that the plane passes through O is not excluded. Referring to figure 2 we introduce the following definitions
Clearly the following two non-collinear vectors belong to the plane
Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors (this is also expressed as: any vector in the plane can be decomposed into components along the two non-collinear vectors). In particular, taking A as origin in the plane,
The real numbers λ and μ specify the direction of . Hence the following equation for the position vector of the arbitrary point P in the plane:
is known as the point-direction representation of the plane. This representation is equal to the three-point representation
where , , and are the position vectors of the three points that define the plane.
Writing for the position vector of the arbitrary point P in the plane
we find that the real triplet (ξ1, ξ2, ξ3) with ξ1 + ξ1 + ξ1 = 1 forms a set of coordinates for P. The numbers {ξ1, ξ2, ξ3 | ξ1+ ξ2+ ξ3 = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation",