Triangle: Difference between revisions
imported>Richard Jensen (point-based definition) |
Pat Palmer (talk | contribs) m (Text replacement - "trigonometry" to "trigonometry") |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
[[Image:Triangle.png|right]] | |||
''This article is about the geometric shape. For the drafting tool, see [[Triangle (tool)]].'' | ''This article is about the geometric shape. For the drafting tool, see [[Triangle (tool)]].'' | ||
| Line 14: | Line 14: | ||
==Properties of triangles== | ==Properties of triangles== | ||
[[Image:TriangleOblique.png|right]] | |||
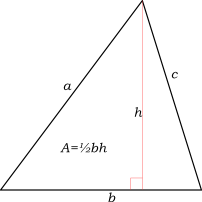
In [[Euclidian geometry]], the sum of the three interior angles of any triangle is 180 degrees. The area of a triangle is equal to one-half times the length of one side times the ''altitude'' relative to that side. (Altitude is the distance of the corner opposite the ''base'' from the line which contains the base. In an obtuse triangle, the altitude may be measured from a point not in the base.) In a right triangle, the base and the altitude are the two sides which meet at the right angle. | |||
[[Heron's formula]] for the area of a triangle uses only the lengths of the sides, and is: | [[Heron's formula]] for the area of a triangle uses only the lengths of the sides, and is: | ||
<math>A = \sqrt{s(s-a)(s-b)(s-c)}</math> where <math>\quad s = \frac{1}{2}(a+b+c),</math> and <math>a, b, c</math> are the lengths of the three sides. | <math>A = \sqrt{s(s-a)(s-b)(s-c)}</math> where <math>\quad s = \frac{1}{2}(a+b+c),</math> and <math>a, b, c</math> are the lengths of the three sides. | ||
A [[circle]] can be drawn through all three vertices of any triangle. The center of the circle lies on the point where the [[perpendicular bisector]]s of the three sides meet. Similarly, a circle can be inscribed within a triangle; the center of the circle lies on the point where the bisectors of the three angles meet. | |||
==Right triangles== | |||
A '''right triangle''' is a triangle where one of the interior angles is a ''right [[angle]]'', measuring 90 degrees (or π/2 [[radian]]s). The two sides which meet at the right angle are called '''legs''', and the remaining side, opposite the right angle, is called the '''hypotenuse'''. | |||
The [[Pythagorean Theorem]] states that the length of the sides of a right triangle are related; where ''a'' and ''b'' are the lengths of the legs, and ''c'' the length of the hypotenuse, <math>a^2 + b^2 = c^2</math>. Cases where a, b, and c are all small integers include the sets {3, 4, 5}, {5, 12, 13}, and {7, 24, 25}. The first relation was known to the ancient Egyptians. | |||
The area of a right triangle with legs ''a'' and ''b'' is <math>A = \tfrac{1}{2}a b</math> | |||
===Trigonometry=== | |||
[[Image:TrigFunc.png|left]] | |||
The relationships between the angles and relative lengths of sides of a right triangle form the basis of [[Trigonometric function|trigonometry]]. Three basic trigonometric functions are defined for an angle between 0 and 90 degrees creating one corner of a right triangle. The '''[[sine]]''' of an angle is the ratio of the length of the opposite leg to the length of the hypotenuse; the '''cosine''' is the ratio of the length of the adjacent leg to the length of the hypotenuse; and the '''tangent''' is the ratio of the length of the opposite leg to the length of the adjacent leg. The '''secant''' is the reciprocal of the cosine, the '''cosecant''' is the reciprocal of the sine, and the '''cotangent''' is the reciprocal of the tangent. | |||
The trigonometric functions have other definitions which allow their use for angles outside the range 0 - 90 degrees, including definitions on a circle, and analytic definitions which do not rely on geometry. | |||
[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 09:09, 16 December 2024
This article is about the geometric shape. For the drafting tool, see Triangle (tool).
A triangle is a two dimensional polygon with three sides meeting at three corners. Alternatively it is three distinct points connected by straight lines called sides.
Several different types of triangles exist:
- An equilaterial triangle is one such that each angle is the same (60 degrees), and each side is of the same length.
- An isosceles triangle is one that has two sides of equal length, and two interior angles equal. In an isosceles triangle, the angles which are formed by the equal sides with the unequal side are equal to each other.
- An obtuse triangle is one that has one angle which is greater than 90 degrees.
- An acute triangle is one such that all three angles are less than 90 degrees.
- A right triangle is one that has one 90 degree angle.
Properties of triangles
In Euclidian geometry, the sum of the three interior angles of any triangle is 180 degrees. The area of a triangle is equal to one-half times the length of one side times the altitude relative to that side. (Altitude is the distance of the corner opposite the base from the line which contains the base. In an obtuse triangle, the altitude may be measured from a point not in the base.) In a right triangle, the base and the altitude are the two sides which meet at the right angle.
Heron's formula for the area of a triangle uses only the lengths of the sides, and is:
where and are the lengths of the three sides.
A circle can be drawn through all three vertices of any triangle. The center of the circle lies on the point where the perpendicular bisectors of the three sides meet. Similarly, a circle can be inscribed within a triangle; the center of the circle lies on the point where the bisectors of the three angles meet.
Right triangles
A right triangle is a triangle where one of the interior angles is a right angle, measuring 90 degrees (or π/2 radians). The two sides which meet at the right angle are called legs, and the remaining side, opposite the right angle, is called the hypotenuse.
The Pythagorean Theorem states that the length of the sides of a right triangle are related; where a and b are the lengths of the legs, and c the length of the hypotenuse, . Cases where a, b, and c are all small integers include the sets {3, 4, 5}, {5, 12, 13}, and {7, 24, 25}. The first relation was known to the ancient Egyptians.
The area of a right triangle with legs a and b is
Trigonometry
The relationships between the angles and relative lengths of sides of a right triangle form the basis of trigonometry. Three basic trigonometric functions are defined for an angle between 0 and 90 degrees creating one corner of a right triangle. The sine of an angle is the ratio of the length of the opposite leg to the length of the hypotenuse; the cosine is the ratio of the length of the adjacent leg to the length of the hypotenuse; and the tangent is the ratio of the length of the opposite leg to the length of the adjacent leg. The secant is the reciprocal of the cosine, the cosecant is the reciprocal of the sine, and the cotangent is the reciprocal of the tangent.
The trigonometric functions have other definitions which allow their use for angles outside the range 0 - 90 degrees, including definitions on a circle, and analytic definitions which do not rely on geometry.