Vector product: Difference between revisions
imported>Paul Wormer |
mNo edit summary |
||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
=== Definition === | === Definition === | ||
Given two vectors, '''A''' and '''B''' in <math>\scriptstyle \mathbb{R}^3</math>, the vector product is a vector with length ''AB'' sin θ<sub>AB</sub>, where ''A'' is the length of '''A''', ''B'' is the length of '''B''', and θ<sub>AB</sub> is the smaller angle between '''A''' and '''B'''. The direction of the vector product is perpendicular (or normal to) the plane containing the vectors '''A''' and '''B''' and follows the right-hand rule | Given two vectors, '''A''' and '''B''' in <math>\scriptstyle \mathbb{R}^3</math>, the vector product is a vector with length ''AB'' sin θ<sub>AB</sub>, where ''A'' is the length of '''A''', ''B'' is the length of '''B''', and θ<sub>AB</sub> is the smaller (non-reentrant) angle between '''A''' and '''B'''. The direction of the vector product is perpendicular (or normal to) the plane containing the vectors '''A''' and '''B''' and follows the [[right-hand rule]], | ||
:<math> | :<math> | ||
\mathbf{A}\times \mathbf{B} = \mathbf{a}_\textrm{N}\, |\mathbf{A}|\, |\mathbf{B}|\,\sin\theta_{AB}, | \mathbf{A}\times \mathbf{B} = \mathbf{a}_\textrm{N}\, |\mathbf{A}|\, |\mathbf{B}|\,\sin\theta_{AB}, | ||
</math> | </math> | ||
where '''a'''<sub>N</sub> is a unit vector normal to the plane spanned by '''A''' and '''B''' in the right-hand rule direction. | where '''a'''<sub>N</sub> is a unit vector normal to the plane spanned by '''A''' and '''B''' in the right-hand rule direction. | ||
We recall that the length of a vector is the square root of the [[dot product]] of a vector with itself, ''A'' ≡ |'''A'''| = ('''A''' ⋅ '''A''' )<sup>1/2</sup> and similarly for the length of '''B'''. | We recall that the length of a vector is the square root of the [[dot product]] of a vector with itself, ''A'' ≡ |'''A'''| = ('''A''' ⋅ '''A''' )<sup>1/2</sup> and similarly for the length of '''B'''. A unit vector has by definition length one. | ||
From the antisymmetry '''A''' × '''B''' = −'''B''' × '''A''' follows that the cross (vector) product of any vector with itself (or another parallel or antiparallel vector) is zero because '''A''' × '''A''' = − '''A''' × '''A''' and the only quantity equal to minus itself is the zero. Alternatively, one may derive this from the fact that sin(0) = 0 (parallel vectors) and sin(180) = 0 (antiparallel vectors). | From the antisymmetry '''A''' × '''B''' = −'''B''' × '''A''' follows that the cross (vector) product of any vector with itself (or another parallel or antiparallel vector) is zero because '''A''' × '''A''' = − '''A''' × '''A''' and the only quantity equal to minus itself is the zero. Alternatively, one may derive this from the fact that sin(0) = 0 (parallel vectors) and sin(180) = 0 (antiparallel vectors). | ||
=== Another formulation == | == The right hand rule == | ||
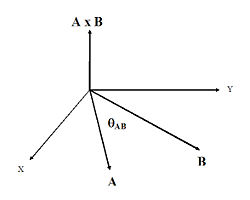
{{Image|CrossProduct.jpg|right|250px|Fig. 1. Diagram illustrating the direction of '''A'''×'''B'''. The plane containing '''A''' and '''B''' is the ''x''-''y'' plane, '''A'''×'''B''' is along the ''z''-axis.}} | |||
The diagram in Fig. 1 illustrates the direction of '''A''' × '''B''', which follows the right-hand rule. If one points the fingers of the right hand towards the head of vector '''A''' (with the wrist at the origin), then curls them towards the direction of '''B''', the extended thumb will point in the direction of '''A''' × '''B'''. | |||
== Another formulation of the cross product== | |||
Rather than in terms of angle and perpendicular unit vector, another form of the cross product is often used. In the alternate definition the vectors must be expressed with respect to a Cartesian (orthonormal) coordinate frame '''a'''<sub>x</sub>, '''a'''<sub>y</sub> and '''a'''<sub>z</sub> of <math>\scriptstyle \mathbb{R}^3</math>. | |||
With respect to this frame we write '''A''' = (''A''<sub>x</sub>, ''A''<sub>y</sub>, ''A''<sub>z</sub>) and '''B''' = (''B''<sub>x</sub>, ''B''<sub>y</sub>, ''B''<sub>z</sub>). Then | |||
'''A''' × '''B''' = (A<sub>y</sub>B<sub>z</sub> - A<sub>z</sub>B<sub>y</sub>)<b>a</b><sub>x</sub> + (A<sub>z</sub>B<sub>x</sub> - A<sub>x</sub>B<sub>z</sub>)<b>a</b><sub>y</sub> + (A<sub>x</sub>B<sub>y</sub> - A<sub>y</sub>B<sub>x</sub>)<b>a</b><sub>z</sub> | :'''A''' × '''B''' = (''A''<sub>y</sub>''B''<sub>z</sub> - ''A''<sub>z</sub>''B''<sub>y</sub>) <b>a</b><sub>x</sub> + (''A''<sub>z</sub>''B''<sub>x</sub> - ''A''<sub>x</sub>''B''<sub>z</sub>) <b>a</b><sub>y</sub> + (''A''<sub>x</sub>''B''<sub>y</sub> - ''A''<sub>y</sub>''B''<sub>x</sub>) <b>a</b><sub>z</sub>. | ||
This formula can be written more concisely upon introduction of a [[determinant]]: | This formula can be written more concisely upon introduction of a [[determinant]]: | ||
<math> | :<math> | ||
\mathbf A \times \mathbf B = | \mathbf A \times \mathbf B = | ||
\left|\begin{array}{ccc} \mathbf a_x & \mathbf a_y & \mathbf a_z \\ | \left|\begin{array}{ccc} \mathbf a_x & \mathbf a_y & \mathbf a_z \\ | ||
| Line 43: | Line 34: | ||
</math> | </math> | ||
where <math>\left|\cdot\right|</math> denotes the determinant of a matrix. | where <math>\left|\cdot\right|</math> denotes the determinant of a matrix. This determinant must be evaluated along the first row, otherwise the equation does not make sense. | ||
==Geometric representation of the length== | |||
We repeat that the length of the cross product of vectors '''A''' and '''B''' is equal to | |||
:<math> | |||
|\mathbf{A}\times \mathbf{B}| = |\mathbf{A}|\, |\mathbf{B}|\,\sin\theta_{AB}, | |||
</math> | |||
because '''a'''<sub>N</sub> has by definition length 1. | |||
{{Image|Cross product.png|left|280px|Fig. 2. The length of the cross product '''A'''×'''B''' is equal to area of the parallelogram with sides ''a'' and ''b'', the sum of the areas of the dotted and dashed triangle.}} | |||
Using the high school geometry rule: the area ''S'' of a triangle is its base ''a'' times its half-height ''d'', we see in Fig. 2 that the area ''S'' of the dotted triangle is equal to: | |||
:<math> | |||
S = \frac{ad}{2} = \frac{|\mathbf{A}| |\mathbf{B}|\sin\theta_{AB}}{2} = \frac{|\mathbf{A}\times \mathbf{B}|}{2}, | |||
</math> | |||
because, as follows from Fig. 2: | |||
:<math> | |||
a = |\mathbf{A}| \quad\textrm{and}\quad d = b \sin\theta_{AB} = |\mathbf{B}|\sin\theta_{AB} . | |||
</math> | |||
Hence |'''A'''×'''B'''| = 2''S''. Since the dotted triangle with sides ''a'', ''b'', and ''c'' is congruent to the dashed triangle, the area of the dotted triangle is equal to the area of the dashed triangle and the length 2''S'' of the cross product is equal to the sum of the areas of the dotted and the dashed triangle. In conclusion: The area of the parallelogram spanned by the vectors '''A''' and '''B''' is equal to the length of '''A'''×'''B'''. | |||
===Application: the volume of a parallelepiped=== | |||
The volume ''V'' of the parallelepiped shown in Fig. 3 is given by | |||
:<math> | |||
V = \mathbf{A}\cdot (\mathbf{B}\times\mathbf{C}). | |||
</math> | |||
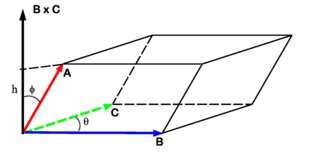
{{Image|Parallelepiped.png|right|320px|Fig. 3. Parallelepiped generated by the vectors | |||
<font color = 'red'> '''A''' </font>, <font color = 'blue'> '''B''' </font>, and <font color = 'green'> '''C''' </font>. Its height is h, the projection of '''A''' on '''B'''×'''C'''.}} | |||
Indeed, remember that the volume of a parallelepiped is given by the area ''S'' of its base times its height ''h'', ''V'' = ''Sh''. Above it was shown that, if | |||
:<math> | |||
\mathbf{D} \equiv \mathbf{B}\times\mathbf{C}\quad\textrm{then}\quad S = |\mathbf{D}|. | |||
</math> | |||
The height ''h'' of the parallelepiped is the length of the projection of the vector '''A''' onto '''D'''. The [[dot product]] between '''A''' and '''D''' is |'''D'''| times the length ''h'', | |||
:<math> | |||
\mathbf{D}\cdot\mathbf{A}= |\mathbf{D}|\,\big(|\mathbf{A}| \cos\phi\big) = |\mathbf{D}|\, h = S h, | |||
</math> | |||
so that ''V'' = ('''B'''×'''C''')⋅'''A''' = '''A'''⋅('''B'''×'''C'''). | |||
[[ | It is of interest to point out that ''V'' can be given by a [[determinant]] that contains the components of '''A''', '''B''', and '''C''' with respect to a Cartesian coordinate system, | ||
:<math> | |||
\begin{align} | |||
V &= \begin{vmatrix} | |||
A_x & B_x & C_x \\ | |||
A_y & B_y & C_y \\ | |||
A_z & B_z & C_z \\ | |||
\end{vmatrix} \\ | |||
&= A_x (B_y C_z - B_z C_y) + A_y(B_z C_x - B_x C_z) + A_z(B_x C_y - B_y C_x). | |||
\end{align} | |||
</math> | |||
From the permutation properties of a determinant follows | |||
:<math> | |||
\mathbf{A}\cdot (\mathbf{B}\times\mathbf{C}) = \mathbf{B}\cdot (\mathbf{C}\times\mathbf{A}) =\mathbf{C}\cdot (\mathbf{A}\times\mathbf{B}). | |||
</math> | |||
The product '''A'''⋅('''B'''×'''C''') is often referred to as a ''[[Triple product|triple scalar product]]''. It is a ''pseudo scalar''. The term scalar refers to the fact that the triple product is invariant under the same simultaneous rotation of '''A''', '''B''', and '''C'''. The term pseudo refers to the fact that simultaneous inversion '''A''' → —'''A''', '''B''' → —'''B''', and '''C''' → —'''C''' converts the triple product into minus itself. | |||
==Cross product as linear map== | |||
Given a fixed vector '''n''', the application of '''n'''× is linear, | |||
:<math> | |||
\mathbf{n}\times( c_1 \mathbf{r}_1 + c_2 \mathbf{r}_2) = c_1 \mathbf{n}\times \mathbf{r}_1 + c_2 \mathbf{n}\times \mathbf{r}_2, \qquad c_1,\, c_2 \in \mathbb{R}. | |||
</math> | |||
This implies that '''n'''×'''r''' can be written as a matrix-vector product, | |||
:<math> | |||
\mathbf{n}\times \mathbf{r} | |||
= \begin{pmatrix} n_y r_z - n_z r_y \\ n_z r_x - n_x r_z \\ n_x r_y - n_y r_x \end{pmatrix} | |||
= \underbrace{ | |||
\begin{pmatrix} | |||
0 & -n_z & n_y \\ | |||
n_z& 0 & -n_x \\ | |||
-n_y& n_x & 0 | |||
\end{pmatrix}}_{\mathbf{N}} \begin{pmatrix} r_x \\ r_y \\ r_z \end{pmatrix} = \mathbf{N}\, \mathbf{r}. | |||
</math> | |||
The matrix '''N''' has as general element | |||
:<math> | |||
N_{\alpha \beta} = -\sum_{\gamma=x,y,z} \epsilon_{\alpha \beta \gamma} n_\gamma \, | |||
</math> | |||
where ε<sub>αβγ</sub> is the antisymmetric [[Levi-Civita symbol]]. | |||
It follows that | |||
:<math> | |||
\left( \mathbf{n}\times \mathbf{r} \right)_\alpha | |||
= \sum_{\beta=x,y,z} N_{\alpha\beta}\; r_\beta = - \sum_{\beta=x,y,z}\sum_{\gamma=x,y,z} \epsilon_{\alpha \beta \gamma} n_\gamma r_\beta = \sum_{\beta=x,y,z}\sum_{\gamma=x,y,z} \epsilon_{\alpha \beta \gamma} n_\beta r_\gamma. | |||
</math> | |||
==Relation to infinitesimal rotation== | |||
The rotation of a vector '''r''' around the unit vector <math>\hat{\mathbf{n}}</math> over an angle φ sends '''r''' to '''r'''′. The rotated vector is related to the original vector by | |||
:<math> | |||
\mathbf{r}' = \mathbf{r}\;\cos\phi + \hat{\mathbf{n}}\;\big(\hat{\mathbf{n}}\cdot \mathbf{r}\big)\big(1-\cos\phi\big) | |||
+ (\hat{\mathbf{n}}\times\mathbf{r} )\;\sin\phi. | |||
</math> | |||
Suppose now that φ is infinitesimal and equal to Δφ, i.e., squares and higher powers of Δφ are negligible with respect to Δφ, then | |||
:<math> | |||
\cos\Delta \phi = 1,\quad\hbox{and}\quad \sin\Delta\phi = \Delta\phi | |||
</math> | |||
so that | |||
:<math> | |||
\mathbf{r}' = \mathbf{r} + \Delta\phi\;(\hat{\mathbf{n}}\times\mathbf{r} ) . | |||
</math> | |||
The linear operator <math>\hat{\mathbf{n}}\times</math> maps <math>\mathbb{R}^3 \rightarrow \mathbb{R}^3 </math> ; it is known as the ''generator of an infinitesimal rotation around'' <math>\hat{\mathbf{n}}</math>. | |||
==Generalization== | ==Generalization== | ||
From a somewhat more abstract point of view one may define the vector product as an element of the antisymmetric subspace of the 9-dimensional tensor product space <math>\scriptstyle \mathbb{R}^3 \otimes \mathbb{R}^3 </math>. This antisymmetric subspace is of dimension 3. | From a somewhat more abstract point of view one may define the vector product as an element of the antisymmetric subspace of the 9-dimensional tensor product space <math>\scriptstyle \mathbb{R}^3 \otimes \mathbb{R}^3 </math>. This antisymmetric subspace is of dimension 3. | ||
In general the antisymmetric subspace of the ''k''-fold tensor power <math>\scriptstyle \mathbb{R}^n \otimes \mathbb{R}^n\otimes \cdots\otimes\mathbb{R}^n </math> is of dimension <math>\scriptstyle {n \choose k}</math>. Elements of such space are often called [[wedge | In general the antisymmetric subspace of the ''k''-fold tensor power <math>\scriptstyle \mathbb{R}^n \otimes \mathbb{R}^n\otimes \cdots\otimes\mathbb{R}^n </math> is of dimension <math>\scriptstyle {n \choose k}</math>. Elements of such space are often called [[exterior products|wedge]] or [[exterior product]]s written as | ||
:<math> | :<math> | ||
A_1 \wedge A_2 \wedge A_3 \cdots \wedge A_k. | A_1 \wedge A_2 \wedge A_3 \cdots \wedge A_k,\qquad A_i \in \mathbb{R}^n, \qquad i=1,\dots,k. | ||
</math> | </math> | ||
The antisymmetric subspace of a two-fold tensor product space is of dimension <math> | The antisymmetric subspace of a two-fold tensor product space is of dimension | ||
:<math>{n \choose 2} = n(n-1)/2</math>. | |||
The latter number is equal to 3 only if ''n'' = 3. For instance, for ''n'' = 2 or 4, the antisymmetric subspaces are of dimension 1 and 6, respectively. | |||
Hence, if one regards the vector product in <math>\scriptstyle \mathbb{R}^3</math> from the point of view of antisymmetric subspaces, it is a "coincidence" that the product lies again in <math>\scriptstyle \mathbb{R}^3</math>. | |||
The cross product lacks the property of a proper vector that it changes sign under inversion [both factors of the cross product change sign and (−1)×(−1) = 1]. A vector that does not change sign under inversion is called an [[axial vector]] or [[pseudo vector]]. Hence a cross product is a pseudo vector. A vector that does change sign is often referred to as a [[polar vector]] in this context. | |||
==External link== | |||
The very first textbook on vector analysis (''Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs'' by Edwin Bidwell Wilson, Yale University Press, New Haven, 1901) can be found [http://www.archive.org/details/117714283 here]. In this book the synonyms: skew product, cross product and vector product are introduced. | |||
[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 12:01, 4 November 2024
A vector product, also known as cross product, is an antisymmetric product A × B = −B × A of two vectors A and B in 3-dimensional Euclidean space . The vector product is again a 3-dimensional vector. The vector product is widely used in many areas of mathematics, mechanics, electromagnetism, gravitational fields, etc.
Definition
Given two vectors, A and B in , the vector product is a vector with length AB sin θAB, where A is the length of A, B is the length of B, and θAB is the smaller (non-reentrant) angle between A and B. The direction of the vector product is perpendicular (or normal to) the plane containing the vectors A and B and follows the right-hand rule,
where aN is a unit vector normal to the plane spanned by A and B in the right-hand rule direction.
We recall that the length of a vector is the square root of the dot product of a vector with itself, A ≡ |A| = (A ⋅ A )1/2 and similarly for the length of B. A unit vector has by definition length one.
From the antisymmetry A × B = −B × A follows that the cross (vector) product of any vector with itself (or another parallel or antiparallel vector) is zero because A × A = − A × A and the only quantity equal to minus itself is the zero. Alternatively, one may derive this from the fact that sin(0) = 0 (parallel vectors) and sin(180) = 0 (antiparallel vectors).
The right hand rule
The diagram in Fig. 1 illustrates the direction of A × B, which follows the right-hand rule. If one points the fingers of the right hand towards the head of vector A (with the wrist at the origin), then curls them towards the direction of B, the extended thumb will point in the direction of A × B.
Another formulation of the cross product
Rather than in terms of angle and perpendicular unit vector, another form of the cross product is often used. In the alternate definition the vectors must be expressed with respect to a Cartesian (orthonormal) coordinate frame ax, ay and az of .
With respect to this frame we write A = (Ax, Ay, Az) and B = (Bx, By, Bz). Then
- A × B = (AyBz - AzBy) ax + (AzBx - AxBz) ay + (AxBy - AyBx) az.
This formula can be written more concisely upon introduction of a determinant:
where denotes the determinant of a matrix. This determinant must be evaluated along the first row, otherwise the equation does not make sense.
Geometric representation of the length
We repeat that the length of the cross product of vectors A and B is equal to
because aN has by definition length 1.
Using the high school geometry rule: the area S of a triangle is its base a times its half-height d, we see in Fig. 2 that the area S of the dotted triangle is equal to:
because, as follows from Fig. 2:
Hence |A×B| = 2S. Since the dotted triangle with sides a, b, and c is congruent to the dashed triangle, the area of the dotted triangle is equal to the area of the dashed triangle and the length 2S of the cross product is equal to the sum of the areas of the dotted and the dashed triangle. In conclusion: The area of the parallelogram spanned by the vectors A and B is equal to the length of A×B.
Application: the volume of a parallelepiped
The volume V of the parallelepiped shown in Fig. 3 is given by
Indeed, remember that the volume of a parallelepiped is given by the area S of its base times its height h, V = Sh. Above it was shown that, if
The height h of the parallelepiped is the length of the projection of the vector A onto D. The dot product between A and D is |D| times the length h,
so that V = (B×C)⋅A = A⋅(B×C).
It is of interest to point out that V can be given by a determinant that contains the components of A, B, and C with respect to a Cartesian coordinate system,
From the permutation properties of a determinant follows
The product A⋅(B×C) is often referred to as a triple scalar product. It is a pseudo scalar. The term scalar refers to the fact that the triple product is invariant under the same simultaneous rotation of A, B, and C. The term pseudo refers to the fact that simultaneous inversion A → —A, B → —B, and C → —C converts the triple product into minus itself.
Cross product as linear map
Given a fixed vector n, the application of n× is linear,
This implies that n×r can be written as a matrix-vector product,
The matrix N has as general element
where εαβγ is the antisymmetric Levi-Civita symbol. It follows that
Relation to infinitesimal rotation
The rotation of a vector r around the unit vector over an angle φ sends r to r′. The rotated vector is related to the original vector by
Suppose now that φ is infinitesimal and equal to Δφ, i.e., squares and higher powers of Δφ are negligible with respect to Δφ, then
so that
The linear operator maps ; it is known as the generator of an infinitesimal rotation around .
Generalization
From a somewhat more abstract point of view one may define the vector product as an element of the antisymmetric subspace of the 9-dimensional tensor product space . This antisymmetric subspace is of dimension 3.
In general the antisymmetric subspace of the k-fold tensor power is of dimension . Elements of such space are often called wedge or exterior products written as
The antisymmetric subspace of a two-fold tensor product space is of dimension
- .
The latter number is equal to 3 only if n = 3. For instance, for n = 2 or 4, the antisymmetric subspaces are of dimension 1 and 6, respectively.
Hence, if one regards the vector product in from the point of view of antisymmetric subspaces, it is a "coincidence" that the product lies again in .
The cross product lacks the property of a proper vector that it changes sign under inversion [both factors of the cross product change sign and (−1)×(−1) = 1]. A vector that does not change sign under inversion is called an axial vector or pseudo vector. Hence a cross product is a pseudo vector. A vector that does change sign is often referred to as a polar vector in this context.
External link
The very first textbook on vector analysis (Vector analysis: a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs by Edwin Bidwell Wilson, Yale University Press, New Haven, 1901) can be found here. In this book the synonyms: skew product, cross product and vector product are introduced.