NMR spectroscopy: Difference between revisions
imported>Sekhar Talluri |
mNo edit summary |
||
| (105 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
''' | {{TOC|right}} | ||
'''NMR spectroscopy''', or nuclear magnetic resonance spectroscopy (also called magnetic resonance spectroscopy, or MRS) is a [[spectroscopy|spectroscopic]] method that uses the [[nuclear magnetic resonance]] principle to manipulate the spin states of atomic nuclei to investigate physical and chemical properties. | |||
NMR spectroscopy | Samples that are typically studied range from single [[atom]]s, [[molecule]]s, molecular clusters, [[protein]]s, nucleic acids, micelles and nanoparticles, up to objects as large as humans (see also [[MRI]]). It manipulates the distribution of energy states by exciting the atoms with electromagnetic radiation that is proportional to both the applied magnetic field and the [[magnetogyric ratio]] of the [[isotope]] studied, and observing the electromagnetic signals emitted as the high energy states relax back to an equilibrium state. | ||
Thus, it does not measure actual atomic energy levels, but instead measures the energy differences between spin states of magnetically active nuclei in the presence of a magnetic field by using radio frequency electromagnetic radiation.<ref> I. I. Rabi.(1937) Phys. Rev., 51 652</ref><ref>N. Bloembergen, E. Purcell and R.V.Pound. (1948). Phys. Rev. 73, 679.</ref> <ref>F. Bloch, W. Hansen, and M.E. Packard, (1946) Phys. Rev. 69, 127.</ref> The energy differences between the spin states of the nuclei depend upon the nature of the atom and are influenced by its environment. However, NMR spectroscopy is not limited to the measurement of energy differences between the spin states, because NMR signals are also influenced by the local motion of the nucleus, the rotational motion of the molecule within which the observed nucleus resides, chemical exchange reactions, and neighboring molecules. Therefore, NMR spectroscopy provides static information, such as global structure, stereochemistry, and composition, as well as dynamic information such as protein folding/unfolding equilibria, chemical exchange rates, molecule diffusion or rotation rates. NMR technology is used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI). | |||
NMR spectroscopy has been used for the study of matter in disordered, ordered and partially ordered systems such as gases, liquids, [[quantum fluids]] | Pulses of radio-frequency electromagnetic radiation can be used to perturb the nuclear spin systems in a variety of ways; the time-dependent response of the system of interest can be recorded and analyzed: | ||
<ref>D.D.Osheroff, W.J.Gully, R.C.Richardson and D.M.Lee, Phys. Rev. Lett. (1972) 29, 920 </ref> <ref>http://nobelprize.org/nobel_prizes/physics/laureates/1996/lee-lecture.pdf </ref>, | * to correlate different spectral properties of nuclei and/or | ||
* to extract information regarding interactions between nuclear spins within the same molecule and/or | |||
* to obtain information regarding intermolecular interactions. | |||
The amplitude, frequency, phase, and duration of pulses of radio-frequency electromagnetic radiation, as well as static and dynamic position-dependent magnetic fields, can be varied in many combinations, giving rise to a wide variety of NMR spectroscopic experiments. | |||
NMR spectroscopic techniques are used extensively for structural elucidation of natural products and for quantitative analysis of components of complex mixtures such as body fluids. However, applications are not limited to these systems; and NMR spectroscopy has been used for the study of matter in disordered, ordered, and partially ordered systems such as gases, liquids, [[quantum fluids]] | |||
<ref>D.D.Osheroff, W.J.Gully, R.C.Richardson and D.M.Lee, Phys. Rev. Lett. (1972) 29, 920 </ref> <ref>http://nobelprize.org/nobel_prizes/physics/laureates/1996/lee-lecture.pdf </ref>, | |||
superconductors, solutions, amorphous solids, crystalline solids, [[liquid crystals]], membranes and living organisms. NMR spectroscopic methods have also found use in [[quantum computing]]. | superconductors, solutions, amorphous solids, crystalline solids, [[liquid crystals]], membranes and living organisms. NMR spectroscopic methods have also found use in [[quantum computing]]. | ||
== | == NMR spectroscopy: Observable parameters == | ||
===The chemical shift=== | |||
The nuclei in molecules are surrounded by electrons. The applied magnetic field induces a circulation of electrons, which in turn produces an additional magnetic field. This effect is called 'shielding', because the magnetic field induced by the circulation of charge is in opposite direction to the field (external) that was responsible for the circulation of charge. Therefore, the nuclei in a given molecule are subjected to a net magnetic field which is the sum of the applied magnetic field and the induced magnetic field. | |||
:<math> | |||
:<math> | |||
B_{induced} = - \sigma B_{applied} \quad \quad \quad | B_{induced} = - \sigma B_{applied} \quad \quad \quad | ||
| Line 52: | Line 27: | ||
B_{net} = B_{applied} + B_{induced} | B_{net} = B_{applied} + B_{induced} | ||
</math> | </math> | ||
where <math>\scriptstyle \sigma </math> is a tensor; however for molecules rotating rapidly in all directions, such as molecules in a gas, liquid or solution, <math> \sigma </math> can be approximated by a scalar and is known as the shielding constant. | where <math>\scriptstyle \sigma </math> is a [[tensor]]; however, for molecules rotating rapidly in all directions, such as molecules in a gas, liquid, or solution, <math> \sigma </math> can be approximated by a scalar and is known as the shielding constant. | ||
<math>\scriptstyle \sigma </math> depends upon the electron density as well as polarizability which vary substantially depending upon the nature of the molecule and the location within the molecule. As a consequence, for a given value of the applied field, nuclei in different molecules and even nuclei in different parts of the same molecule may encounter different net values of the magnetic field | <math>\scriptstyle \sigma </math> depends upon the electron density as well as polarizability, which vary substantially depending upon the nature of the molecule and the location within the molecule. As a consequence, for a given value of the applied field, nuclei in different molecules and even nuclei in different parts of the same molecule may encounter different net values of the magnetic field. This results in a variation in the resonance frequency. | ||
:<math> | :<math> | ||
\nu_{i} = \frac{ \ | \nu_{i} = \frac{ \gamma_el B_{net,i}}{2 \pi } | ||
</math> | </math> | ||
where <math>\scriptstyle \nu_{i} </math> is the resonance frequency for the nucleus labeled 'i' and | where <math>\scriptstyle \nu_{i} </math> is the resonance frequency for the nucleus labeled ''i'', <math>\scriptstyle B_{net,i} </math> is the net magnetic field at nucleus ''i'', and | ||
<math>\scriptstyle \ | <math>\scriptstyle \gamma_el </math> is the [[magnetogyric ratio]] of the isotope of interest. | ||
The relative change in the resonance frequency is called the chemical shift. | The relative change in the resonance frequency is called the chemical shift<ref> W.G. Proctor, F.C. Yu (1950) Phys.Rev. 77, 717. </ref><ref> W.C.Dickinson. (1950) Phys. Rev. 77, 736. </ref><ref>N.F.Ramsey. (1950) Phys. Rev. 78, 699.</ref><ref>N.F.Ramsey. (1952) Phys. Rev. 86, 243. </ref>. | ||
:<math> | :<math> | ||
\delta_{i} (ppm) = \frac{( \nu_{i} - \nu_{ref} ) * 10^6 }{ \nu_{ref} } | \delta_{i} </math>(ppm) <math>= \frac{( \nu_{i} - \nu_{ref} ) * 10^6 }{ \nu_{ref} } | ||
</math> | </math> | ||
where <math>\scriptstyle \nu_{ref} </math> is the resonance frequency of a standard. | where <math>\scriptstyle \nu_{ref} </math> is the resonance frequency of a standard. | ||
The chemical shift <math> \delta </math> is generally quoted in [[ppm]]. | The chemical shift <math> \delta </math> is generally quoted in [[ppm]]. The ppm scale is used because ppm values are field-independent, thus giving the same results on different magnets, and because comparing (field-dependent) numbers like 900.000000003 vs 899.9999997 MHz is inconvenient. As these small changes indicate, the magnetic fields utilized in high-resolution NMR must be constant within parts per billion. | ||
For proton NMR spectroscopy of organic compounds, [[tetramethylsilane]](TMS) was chosen as the reference. It is often used as an internal standard. However, TMS has low solubility in aqueous solution; therefore, it is often necessary to use a secondary standard such as DSP. | |||
The chemical shifts of functional groups in many molecules have been measured, and they provide a basis for identification of functional groups in novel molecules. | |||
The | |||
=== Signal area === | |||
The area of a signal is proportional to the total number of contributing nuclei. For example, in the 1H NMR spectrum of a pure compound containing a single [[methyl]] group and a single [[methylene]] group, the relative areas of the corresponding signals will be in the ratio 3:2, because there are 3 protons in the methyl group and 2 in the methylene group. | |||
If the pure compound can exist in multiple conformations, and if the transitions between the different conformational states occur on a time scale that is slow with reference to the relevant NMR time scale (typically milliseconds), then it may be possible to observe separate signals corresponding to the different conformations in the NMR spectrum. In such a case, the relative areas of the signals corresponding to different conformations will be proportional to the fractions of the molecules that exist in each conformational state during the time that the NMR spectrum was acquired. | |||
Many small molecules can exist in multiple conformations due to rotation about single bonds, however, such rotation is generally rapid at room temperature and hence separate signals are usually not observed for the different rotational isomers that exist at equilibrium. For large molecules, e.g., proteins, the close packing of the constituent amino acids results in restricted rotation about many single bonds and complete loss of conformational freedom for many other single bonds. Such restricted rotation about single bonds results in separate NMR signal for each conformer, and the areas of the NMR signals are again proportional to the populations of the conformers. | |||
In the NMR spectra of mixtures, the relative areas of signals can be used to deduce information regarding the relative concentration of each compound. The very high resolution of NMR spectra enables us to resolve a very large number of compounds, and hence determine the relative concentrations of a large number of chemical species. This is of particular use in vivo spectroscopy and NMR-based [[metabolomics]] studies in which blood plasma or serum, urine, cerebral spinal fluid, or tissue extracts can be studied for metabolic disorders or chemical injury. The ability to resolve the signals of a large number of chemicals/biochemicals can be enhanced significantly by using 2D NMR, but often using methods like targeted profiling, statistical analysis, principal components analysis and other techniques can be used to identify many substances. | |||
Systems undergoing physical and chemical changes can also be monitored by NMR spectroscopy as the interconverting species usually have different chemical shifts. The changes in the relative areas of the reactants and products can be used to obtain information regarding the time course of the reaction. This is possible if the time scale of the conversion is slow with respect to the NMR time scale. Systems which interconvert very fast compared to the NMR data acquisition time are observed as a single, averaged single entity, while those exchanging at about the same time frame can be broadened out so that no (direct) signal is observed. | |||
=== | ===J-coupling and multiplicity=== | ||
J-coupling, also known as scalar coupling, | J-coupling, also known as scalar coupling, causes splitting of NMR signals due to the interactions between different nuclei in the same molecule that are mediated through electrons in chemical bonds<ref> H.S.Gutowsky, D.W.McCall, C.P.Slichter (1951) Phys. Rev. 84, 589. </ref><ref> N.F.Ramsey. (1953) Phys. Rev. 91, 303. </ref><ref>M.Karplus (1963). J. Am. Chem. Soc. 30, 11.</ref>. Usually, the J-coupling interaction is observable between nuclei that are separated from each other by three or fewer bonds. If the coupling is weak the resulting pattern is a function of the number of neighboring nuclei, and this information plays a critical role in structural elucidation of small organic molecules. In addition, the magnitude of the line-splitting (coupling constant) provides information regarding the molecular conformation. | ||
For weak coupling, the multiplicity of a signal is expected to be 2''nI'' + 1 where ''n'' is the number of nuclei with spin angular momentum quantum number (spin) ''I'' that have J coupling with the nucleus responsible for the signal being observed. If all magnetically active nuclei are protons, then the multiplicity is equal to ''n'' + 1, because ''I'' = 1/2 for protons. In addition, the relative intensities of the peaks within a multiplet is given by the coefficients of the [[binomial expansion]]. This is known as the ''n'' + 1 rule. | |||
In using the n+1 rule, couplings between magnetically equivalent nuclei are not considered because the effects of J-coupling are not observable in a normal 1D NMR spectrum if the nuclei involved in the interaction are [[magnetically equivalent]]. | In using the ''n'' + 1 rule, couplings between magnetically equivalent nuclei are not considered because the effects of J-coupling are not observable in a normal 1D NMR spectrum if the nuclei involved in the interaction are [[chemical and magnetic equivalence | magnetically equivalent]]. | ||
For example, in the fragment CH3-CH2-O-, the signal corresponding to the methyl (CH3) protons will have a multiplicity of three, because each of the methyl hydrogen has a J-coupling to each of the two (equivalent) methylene (CH2) protons, hence ''n'' = 2, ''I'' = 1/2, and 2''nI'' + 1 = 3. | |||
The signal corresponding to the methylene group of protons will be a quartet, as each methylene proton is expected to have J coupling to each of the three methyl (CH3) protons, hence n=3, I=1/2 and | The signal corresponding to the methylene group of protons will be a quartet, as each methylene proton is expected to have J coupling to each of the three methyl (CH3) protons, hence ''n'' = 3, ''I'' = 1/2, and 2''nI'' + 1 = 4. In this case, the pairs of nuclei that have observable J-coupling are separated by three bonds. Note that interactions between magnetically equivalent nuclei, such as interactions between the different protons of the same methyl group (separated by only two bonds), need not be considered when predicting the multiplicity. In this example the three protons in the methyl group are treated as magnetically equivalent and the two protons in the methylene group are treated as magnetically equivalent by assuming that free rotation occurs about the single bond separating the methyl and methylene groups. If this is not the case, e.g., if restricted rotation occurs about the single bond and if the fragment is placed in an asymmetric environment (such as part of a rigid macromolecule), then the methylene protons may no longer be assumed to be magnetically equivalent. | ||
The | The 2''nI'' + 1 rule assumes that all of the neighboring geminal nuclei (i.e., those with observable J-coupling to nucleus being observed) are equivalent. If this is not the case, then the multiplet structure can still be predicted by considering first the coupling to one set of equivalent J-coupled nuclei and predicting that the effect of the remaining nuclei will cause additional splitting of the multiplet generated by interaction with the first set. | ||
The magnitude of the J-coupling depends on the number of bonds separating the interacting nuclei as well as on the geometry. For <sup>3</sup>J coupling, i.e., coupling between nuclei separated by three bonds, the magnitude of the coupling between the interacting nuclei is given by the Karplus equation | The magnitude of the J-coupling depends on the number of bonds separating the interacting nuclei as well as on the geometry. For <sup>3</sup>J coupling, i.e., coupling between nuclei separated by three bonds, the magnitude of the coupling between the interacting nuclei is given by the Karplus equation | ||
: <math> ^3J = A + B \cos{\theta} + C \cos^2{\theta} \qquad or \qquad ^3J = A + B \cos{\theta} + C \cos{2\theta} </math> | : <math> ^3J = A + B \cos{\theta} + C \cos^2{\theta} \qquad or \qquad ^3J = A + B \cos{\theta} + C \cos{2\theta} </math> | ||
where | where θ is the dihedral angle involving the nuclei of interest. The values of ''A,B'' and ''C'' depend on the chemical nature of the fragment. The Karplus equation is useful for conformational analysis of molecules, particularly biopolymers such as polypeptides<ref>V.F.Bystrov. Progress in NMR Spectroscopy, (1976) 10, 41-82</ref> and nucleic acids. The parameters ''A,B'' and ''C'' of the Karplus equation have been determined for most combinations of nuclei that occur in organic compounds, by comparing experimental NMR and X-ray crystallographic data. If relevant experiment data is not available, the magnitude of the J coupling may be calculated by using quantum chemical calculations<ref>H.Fukui. Progress in NMR spectroscopy (1999) 35, 267-294</ref>; however the prediction accuracy of ab initio calculations is often lower than that obtained from empirical parametrization. | ||
=== The net magnetization vector=== | |||
In the presence of an external magnetic field '''B''', the distribution of the number of nuclei in the different allowed nuclear spin states follows the Boltzmann distribution at equilibrium. i.e. for a two state system with states <math> \alpha </math> and <math> \beta </math> | In the presence of an external magnetic field '''B''', the distribution of the number of nuclei in the different allowed nuclear spin states follows the Boltzmann distribution at equilibrium. i.e. for a two state system with states <math> \alpha </math> and <math> \beta </math> | ||
| Line 107: | Line 82: | ||
: <math> n_{\beta} = </math> number of nuclei in state <math> \beta </math>; <math>n_{\alpha} = </math> number of nuclei in state <math> \alpha </math> | : <math> n_{\beta} = </math> number of nuclei in state <math> \beta </math>; <math>n_{\alpha} = </math> number of nuclei in state <math> \alpha </math> | ||
: <math>E_\beta = </math> Energy of state <math> \beta </math>; <math>E_\alpha = </math> Energy of state <math> \alpha</math> | : <math>E_\beta = </math> Energy of state <math> \beta </math>; <math>E_\alpha = </math> Energy of state <math> \alpha</math> | ||
: T = Absolute temperature in Kelvin; <math>\quad</math> k=Boltzmann constant | : ''T'' = Absolute temperature in Kelvin; <math>\quad</math> k = Boltzmann constant | ||
If the energy of state <math> \beta </math> is greater than that of state <math> \alpha </math>, then fewer nuclei will be present in the higher energy state <math> \beta </math>. However, since the energy difference between these two states is small the population difference is quite small and the macroscopically observable net magnetization vector for the entire population will be the vectorial sum of the magnetic moments of all the nuclei present in the sample. | If the energy of state <math> \beta </math> is greater than that of state <math> \alpha </math>, then fewer nuclei will be present in the higher energy state <math> \beta </math>. However, since the energy difference between these two states is small the population difference is quite small and the macroscopically observable net magnetization vector for the entire population will be the vectorial sum of the magnetic moments of all the nuclei present in the sample. | ||
At equilibrium, in a homogeneous magnetic field, although the orientation of the spin magnetic moments of individual nuclei is restricted to certain directions with respect to the applied magnetic field, there is no preference for any direction for the projection of the magnetic moment onto the x-y plane. | At equilibrium, in a homogeneous magnetic field, although the orientation of the spin magnetic moments of individual nuclei is restricted to certain directions with respect to the applied magnetic field (which usually defines the ''z'' axis), there is no preference for any direction for the projection of the magnetic moment onto the x-y plane. The X- and Y-components of the net magnetization vector of the sample should be zero at equilibrium because the X- and Y-components of the spin magnetic moments of individual nuclei are randomly oriented and the net magnetization vector is the vectorial sum of the spin magnetic moments of individual nuclei. Therefore, the equilibrium magnetization will be | ||
: <math> M_{equil} = M_{z,equil} = N <\mu_{z}> = \frac{N\sum{g_i \mu_{zi}e^{-\frac{E_i}{kT}}}}{\sum{g_i e^{-\frac{E_i}{kT}}}}</math> | : <math> M_{equil} = M_{z,equil} = N <\mu_{z}> = \frac{N\sum{g_i \mu_{zi}e^{-\frac{E_i}{kT}}}}{\sum{g_i e^{-\frac{E_i}{kT}}}}</math> | ||
where | where | ||
: N = total number of nuclei in sample; <math> M_{equil} = </math> Magnetization vector (net) at equilibrium | : ''N'' = total number of nuclei in sample; <math> M_{equil} = </math> Magnetization vector (net) at equilibrium | ||
: <math>E_i = </math> energy of state i; <math>\quad \quad \quad \mu_{zi} = </math> z-component of magnetic moment of state i | : <math>E_i = </math> energy of state i; <math>\quad \quad \quad \mu_{zi} = </math> z-component of magnetic moment of state i | ||
: <math>g_i = </math> degeneracy of state i | : <math>g_i = </math> degeneracy of state i | ||
For a two state system, the <math> \mu_{zi} </math> are equal in magnitude but opposite in direction. However, there are more nuclei in the lower energy state at the temperature of the experiment T, hence the numerator in the sum above is nonzero. Therefore, at equilibrium, the net magnetization vector has only one non-zero component (the <math> M_{z,equil}</math>-component) when the system is placed in a static homogeneous magnetic field. | For a two-state system, the <math> \mu_{zi} </math> are equal in magnitude but opposite in direction. However, there are more nuclei in the lower energy state at the temperature of the experiment T, hence the numerator in the sum above is nonzero. Therefore, at equilibrium, the net magnetization vector has only one non-zero component (the <math> M_{z,equil}</math>-component) when the system is placed in a static homogeneous magnetic field. | ||
In the presence of homogeneous magnetic field (possibly time dependent), represented by the vector '''B''', the magnetization vector experiences a torque and the time dependence of the net magnetization vector '''M''' (neglecting relaxation effects) is | In the presence of homogeneous magnetic field (possibly time dependent), represented by the vector '''B''', the magnetization vector experiences a torque and the time dependence of the net magnetization vector '''M''' (neglecting relaxation effects) is | ||
: <math> \frac{dM}{dt} = M \times \gamma B </math> | : <math> \frac{dM}{dt} = M \times \gamma B </math> | ||
The | The [[Bloch equations]] describe the time dependence of the different components of the net magnetization vector subject to relaxation, in the presence of a time-dependent magnetic field. | ||
==== | ===Relaxation time=== | ||
I. Solomon. (1955). Phys. Rev. 99, 559.</ref> | After a collection of nuclei in a magnetic field that is at equilibrium with its surroundings is perturbed in some manner (usually by a pulse of electromagnetic radiation), the system requires a certain amount of the time to return to equilibrium. If this process is exponential, the rate constant is called relaxation rate. The relaxation rate is inversely proportional to relaxation time<ref>N. Bloembergen, E. Purcell and R.V.Pound. (1948). Phys. Rev. 73, 679.</ref> <ref>F. Bloch, W. Hansen, and M.E. Packard, (1946) Phys. Rev. 69, 127.</ref> <ref>I. Solomon. (1955). Phys. Rev. 99, 559.</ref>. ''T1 relaxation time'' characterizes the return to equilibrium of the longitudinal component of the magnetization of the collection of nuclei. Similarly, ''T2 relaxation time'' characterizes the return to equilibrium of the transverse component of the magnetization of the collection of nuclei that are being studied. In a static homogeneous magnetic field, the transverse component of the net magnetization vector for a sufficiently large collection of nuclei is always zero, at equilibrium. | ||
The dominant mechanism of relaxation is usually the dipolar interaction with the closest neighbor. For a pair of identical spins separated by a distance <math> r </math>, in a homogeneous magnetic field, undergoing isotropic rotational motion in solution, the relaxation rates are: | The dominant mechanism of relaxation is usually the dipolar interaction with the closest neighbor. For a pair of identical spins separated by a distance <math> r </math>, in a homogeneous magnetic field, undergoing isotropic rotational motion in solution, the relaxation rates are: | ||
: <math> \frac{1}{T_1} = \frac{\gamma^4\hbar^2}{10 r^6 } ( 3J(w_o) + 12 J(2w_o) ) </math> | : <math> \frac{1}{T_1} = \Big(\frac{\mu_0}{4 \pi}\Big)^2 \quad \frac{\gamma^4\hbar^2}{10 r^6 } ( 3J(w_o) + 12 J(2w_o) ) </math> | ||
: <math> \frac{1}{T_2} = \frac{\gamma^4\hbar^2}{20 r^6 } ( 9J(0) + 15J(w_o) + 6 J(2w_o) ) </math> | |||
: where <math> J(w) = \frac{\tau_c}{1+w^2\tau_c^2} </math> is the spectral density function | : <math> \frac{1}{T_2} = \Big(\frac{\mu_0}{4 \pi}\Big)^2 \quad \frac{\gamma^4\hbar^2}{20 r^6 } ( 9J(0) + 15J(w_o) + 6 J(2w_o) ) </math> | ||
: | |||
: where <math> J(w) = \frac{\tau_c}{1+w^2\tau_c^2} </math> is the spectral density function | |||
: <math> \tau_c </math> is the mean time required for rotational motion of the pair of nuclei by one radian | : <math> \tau_c </math> is the mean time required for rotational motion of the pair of nuclei by one radian | ||
: <math> \mu_0 </math> is the magnetic permeability of [[Free space (electromagnetism)|free space]] | |||
: <math> \gamma </math> is the gyromagnetic ratio and | : <math> \gamma </math> is the gyromagnetic ratio and | ||
: <math> \hbar </math> is the Planck's constant divided by <math> 2 \pi </math>. | : <math> \hbar </math> is the Planck's constant divided by <math> 2 \pi </math>. | ||
For a pair of nonidentical spins I and S, : | For a pair of nonidentical spins ''I'' and ''S,'' separated by a distance ''r'', the time dependence of the expectation values of the ''z''-components of magnetization are given by the Solomon equations: | ||
: <math> \frac{d<I_z>}{dt} = -\rho_I (<I_z> - <I_{z,equil}>) - \sigma (<S_z> - <S_{z,equil}>) | : <math> | ||
\begin{align} | |||
\frac{d<I_z>}{dt} = -\rho_I (<I_z> - <I_{z,equil}>) - \sigma (<S_z> - <S_{z,equil}>) \\ | |||
: < | \frac{d<S_z>}{dt} = -\rho_S (<S_z> - <S_{z,equil}>) - \sigma (<I_z> - <I_{z,equil}>) | ||
\end{align} | |||
</math> | |||
<math>\rho </math> and <math> \sigma </math> are the auto- and cross relaxation rates, respectively. <math> \sigma </math> and is responsible for the [[Nuclear overhauser effect]]. | |||
: <math> | |||
\begin{align} | |||
\rho_I &= \Big(\frac{\mu_0}{4 \pi}\Big)^2\quad\frac{\gamma_I^2\gamma_S^2\hbar^2}{10 r^6 } ( J(w_I-w_S) + 3J(w_I) + 6 J(w_I + w_S) ) \\ | |||
==== | \sigma &= \Big(\frac{\mu_0}{4 \pi}\Big)^2\quad\frac{\gamma_I^2\gamma_S^2\hbar^2}{10 r^6 } ( -J(w_I-w_S) + 6 J(w_I + w_S) )) \\ | ||
Irradiation at the resonance frequency of one nucleus in the molecule may cause changes in the intensity of a signal at a different frequency corresponding to another | |||
The Noe enhancement, <math>\eta</math>, in the steady state, when the resonance frequency of spin I is irradiated and the intensity of spin S is monitored is | \frac{1}{T_2} &= \Big(\frac{\mu_0}{4 \pi}\Big)^2\quad\frac{\gamma_I^2\gamma_S^2\hbar^2}{20 r^6 } ( 4J(0) + J(w_I - w_S) + 3J(w_I) + 6 J(w_I + w_S) + 6 J(w_S) ) \\ | ||
\end{align} | |||
</math> | |||
A homogeneous magnetic field, isotropic rotational motion, and negligible chemical shift anisotropy are assumed in the derivation of the equations described above. | |||
=== Dipolar coupling and nuclear Overhauser effect === | |||
Irradiation at the resonance frequency of one nucleus in the molecule may cause changes in the intensity of a signal at a different frequency corresponding to another nucleus—this is called the [[Nuclear Overhauser effect |nuclear Overhauser effect]]<ref>A.W.Overhauser (1953). Phys. Rev. 92, 411 </ref> (Noe). The nuclear Overhauser effect is due to dipole–dipole interactions between the magnetic moments of a pair of nuclei. Unlike J-coupling, this interaction is not mediated through bonds. Hence, it may be possible to observe the nuclear Overhauser effect between pairs of nuclei separated by many bonds, provided that they are in spatial proximity. The strength of the observable nuclear Overhauser effect for molecules in solution is proportional to the inverse of the sixth power of the distance between the two nuclei due to averaging caused by rotational motion. Both the magnitude as well as the sign of the nuclear Overhauser effect depend on the rotational frequencies of the pair of nuclei with respect to the applied magnetic field. | |||
The Noe enhancement, <math>\eta</math>, in the steady state, when the resonance frequency of spin ''I'' is irradiated and the intensity of spin ''S'' is monitored is | |||
<math>\eta</math> = (<math>\sigma</math> <math>\gamma</math><sub>I</sub> )/ (<math>\rho</math><sub>S</sub> <math>\gamma</math><sub>S</sub>). | <math>\eta</math> = (<math>\sigma</math> <math>\gamma</math><sub>I</sub> )/ (<math>\rho</math><sub>S</sub> <math>\gamma</math><sub>S</sub>). | ||
This indicates that considerable enhancement in the intensity of the S signal can be obtained by irradiation at the frequency of the I spin, provided that | This indicates that considerable enhancement in the intensity of the ''S'' signal can be obtained by irradiation at the frequency of the ''I'' spin, provided that | ||
<math>\gamma</math><sub>I</sub>/<math>\gamma</math><sub>S</sub> is greater than 1, | <math>\gamma</math><sub>I</sub>/<math>\gamma</math><sub>S</sub> is greater than 1, | ||
because <math>\sigma</math>/<math>\rho</math><sub>S</sub> is approximately 1/2 | because <math>\sigma</math>/<math>\rho</math><sub>S</sub> is approximately 1/2 | ||
when w<math>\tau_c</math> is much smaller than 1 . | when w<math>\tau_c</math> is much smaller than 1 . | ||
However, when w<math>\tau_c</math> is much greater than 1, | |||
<math>\sigma</math>/<math>\rho</math><sub>S</sub> approaches –1 and negative Noe enhancements are obtained. | |||
The sign of <math>\eta</math> changes from positive to negative when w<math>\tau_c</math> is close to 1 and under such conditions the Noe effect may not be observable. This happens for rigid molecules with relative molecular mass about 500 at room temperature, e.g., many hexapeptides. | |||
For most molecules (in isotropic media, at room temperature), direct observation of dipolar coupling in solution NMR spectra (as a separation of the components of a signal) is not possible, because dipolar interactions are averaged over all orientations of the molecule. However, it is possible to obtain partial alignment of macromolecules using anisotropic media, leading to incomplete averaging of the dipolar interactions. In such cases there is an 'apparent' change in the measured values of J-coupling constants because the '''residual dipolar coupling''' has the same form as the weak scalar coupling Hamiltonian. For a pair of nuclei, at a fixed distance, the magnitude and signs of the [[residual dipolar coupling]]s are angle dependent. Hence, measurements of residual dipolar couplings (RDC) can be used to obtain angular constraints (used for structure determination). | |||
== Instrumentation == | |||
A typical NMR spectrometer contains three components: (1) magnet (2) [[probe]] (3) [[RF electronics]]. | |||
For any system at [[equilibrium]] in the absence of a magnetic field, all the nuclear spin states are equally populated and hence there is no net [[polarization]] due to the nuclear spins. Therefore, it is necessary to introduce an external [[magnetic field]] which leads to preferential population of the lower energy nuclear spin states. The energy differences between the different nuclear spin states are proportional to the strength of the magnetic field. Therefore, higher magnetic fields lead to greater separation between the energy levels and greater polarization at equilibrium. The required magnetic field is usually provided by an external magnet. | |||
High [[magnetic field]]s (1–17 tesla) are generally preferred for high resolution, high sensitivity NMR spectroscopic experiments. In general, higher magnetic fields provide higher signal-to-noise ratio as well as higher resolution. Most high resolution NMR spectrometers used by chemists and biologists use superconducting magnets. However, NMR spectrometers with lower resolution may use permanent magnets or electromagnets. It is also feasible to carry out certain types of NMR experiments in much weaker fields—in fact many NMR spectroscopic experiments have been conducted using the earth's magnetic field. | |||
The probe in an NMR spectrometer is responsible for coupling the radio frequency electromagnetic field generated by the RF electronics to the sample. It is also responsible for detecting the NMR signal (through induction) and passing it to the receiver. | |||
RF electronics consists of two basic subsystems: The transmitter and the receiver subsystems. | |||
Transmitter subsystem: The transmitter subsystem is responsible for generating a radio frequency signal in the form of a sequence of pulses with specified [[frequency]], [[amplitude]], [[phase]], and duration for each pulse. It consists of the RF synthesizers and amplifiers. This subsystem is responsible for generating waveforms of the required frequency, amplitude, phase, and duration at specified times. Multiple RF synthesizers are required because many MR experiments require simultaneous application of RF pulses of different frequency. Earlier MR systems used waveform generators with subsequent phase modulation. However, more recent systems rely on DDS (direct digital synthesis). | |||
RF switch is responsible for coupling either the Transmitter or the Receiver subsystem to the probe. This ensures that the sensitive receiver subsystem is not overloaded with the high-powered RF signal generated by the transmitter system. Also, the receiver is 'blanked' during the transmission and for a short duration afterward. | |||
Receiver subsystem: The receiver subsystem is responsible for amplification of the NMR signal and for its conversion to a lower frequency so that the signal can be digitized. This consists of the components: preamplifier, amplifier, demodulator, and the analog-to-digital converter (ADC). The demodulator is responsible for subtracting a reference frequency of specified phase from the observed signal. | |||
Magnetic field gradients of specified strength and duration are generated by passing current through coils of appropriate geometry. Magnetic field gradients are controlled by an independent subsystem. | |||
== Pulsed ( | Shimming is the process that corrects for spatial inhomogeneities in the magnetic field. | ||
Field frequency lock is used to keep the magnetic field fixed at a specified value during the duration of the experiment. | |||
== Pulsed (radio frequency) NMR spectroscopy == | |||
=== Spin echoes === | === Spin echoes === | ||
A pulse of | A pulse of radio frequency (RF) radiation is applied for sufficient duration to tip the net magnetization vector into the ''x–y'' plane; this is followed by a short delay <math> \tau </math>, followed by another RF pulse that inverts the magnetization around the ''x''-axis, followed by another short delay <math>\tau</math>. The magnetization at the end of this pulse-sequence is | ||
: <math> M(2\tau) = M_o e^{-\frac{2\tau}{T_2}} </math> | : <math> M(2\tau) = M_o e^{-\frac{2\tau}{T_2}} </math> | ||
The transverse relaxation time can be measured by repeating the experiment with different value of <math> \tau </math>, and plotting <math> log_eM(2\tau) </math> vs <math> 2\tau </math>. The resulting plot is expected to be a straight line with slope <math> -1/T_2 </math>. | The transverse relaxation time can be measured by repeating the experiment with different value of <math> \tau </math>, and plotting <math> log_eM(2\tau) </math> vs <math> 2\tau </math>. The resulting plot is expected to be a straight line with slope <math> -1/T_2 </math>. | ||
| Line 171: | Line 184: | ||
If the above experiment is carried out with a magnetic field gradient during the two delays <math> \tau </math> then | If the above experiment is carried out with a magnetic field gradient during the two delays <math> \tau </math> then | ||
: <math> M(2\tau) = M_o e^{-\frac{2\tau}{T_2}}e^{-\frac{2DG^2\tau^3}{3}} </math> | : <math> M(2\tau) = M_o e^{-\frac{2\tau}{T_2}}e^{-\frac{2DG^2\tau^3}{3}} </math> | ||
where D is the diffusion coefficient and G is the magnetic field gradient. Repeating this experiment with different values of G enables us to measure the | where ''D'' is the diffusion coefficient and ''G'' is the magnetic field gradient. Repeating this experiment with different values of ''G'' enables us to measure the diffusion coefficient ''D''. | ||
=== | ===Fourier transform NMR spectroscopy=== | ||
Fourier transform NMR spectroscopy (Ernst <ref>R.R.Ernst, Nobel lecture</ref><ref>R.R. Ernst and W.A. Anderson, (1966) Rev. Sci. Instrum. 37, 93</ref>) : A pulse (or a pulse train) of | Fourier transform NMR spectroscopy (Ernst <ref>R.R.Ernst, Nobel lecture</ref><ref>R.R. Ernst and W.A. Anderson, (1966) Rev. Sci. Instrum. 37, 93</ref>) is performed in the following way: A pulse (or a pulse train) of electromagnetic radiation is used to cause a perturbation in the system. The time-dependent response of the system is recorded (this time-dependent response is often referred to as the free induction decay, abbreviated as fid). A [[fourier transform]] of the response gives information regarding the frequency response. | ||
In the case of a single pulse perturbation, the fourier transform of the time dependent response is equivalent to a 1D NMR spectrum. | In the case of a single pulse perturbation, the [[fourier transform]] of the time-dependent response is equivalent to a 1D NMR spectrum. | ||
| Line 181: | Line 194: | ||
|- | |- | ||
! fid | ! fid | ||
! | ! | ||
! NMR spectrum | ! NMR spectrum | ||
|- | |- | ||
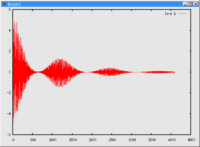
| [[Image:Fid.png|left|thumb|200px|<br/> | free induction decay ]] | | [[Image:Fid.png|left|thumb|200px|<br/> | free induction decay ]] | ||
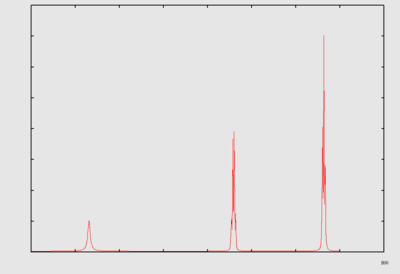
| | | FT{FID} → spectrum. | ||
| [[Image:Ethanolzoom.png|right|thumb|400px|<br/>| NMR Spectrum ]] | | [[Image:Ethanolzoom.png|right|thumb|400px|<br/>| NMR Spectrum ]] | ||
|- | |- | ||
|} | |} | ||
===Multidimensional NMR spectroscopy=== | |||
Multidimensional NMR spectroscopy (nD NMR; Jeener <ref>J. Jeener. (1971). Unpublished lectures at the Ampere International Summer School II, Basko Polje, Yugoslavia.</ref>; Aue et al.<ref name=Aue1976>{{citation | |||
=== | | last = Aue | first = W. P. | ||
| year = 1976 | |||
The nuclei in a magnetic field are subjected to a series of pulses of electromagnetic radiation separated by delays. The time dependent response of the system is recorded. The delays between the pulses may be fixed or incremented systematically between different repetitions of the experiment. The number of variable delays determines the dimensionality of the experiment. A multidimensional Fourier Transform of the entire data set characterizes the frequency responses of the system and enables a correlation between different NMR parameters. | | title = Two-dimensional spectroscopy. Application to nuclear magnetic resonance | ||
Different combinations of the pulses and delays known as 'pulse sequences' enable us to correlate and measure different types of NMR parameters. Some common examples of multidimensional NMR spectroscopy experiments (2D, 3D and 4D): COSY, NOESY, TOCSY, EXSY, HSQC, HNHA, HSQC-NOESY, HNCA, HNCO, HNCACO, HSQC-NOESY-HSQC | | journal = The Journal of Chemical Physics | ||
| volume = 64 | |||
| pages = 2229-2246 | |||
| doi = 10.1063/1.432450 | |||
| url = http://link.aip.org/link/?JCPSA6/64/2229/1 | |||
}}</ref>) | |||
The nuclei in a magnetic field are subjected to a series of pulses of electromagnetic radiation separated by delays. The time-dependent response of the system is recorded. The delays between the pulses may be fixed or incremented systematically between different repetitions of the experiment. The number of variable delays determines the dimensionality of the experiment. A multidimensional Fourier Transform of the entire data set characterizes the frequency responses of the system and enables a correlation between different NMR parameters. | |||
Different combinations of the pulses and delays known as 'pulse sequences' enable us to correlate and measure different types of NMR parameters. Some common examples of multidimensional NMR spectroscopy experiments (2D, 3D and 4D) include: COSY, NOESY, TOCSY, EXSY, HSQC, HNHA, HSQC-NOESY, HNCA, HNCO, HNCACO, HSQC-NOESY-HSQC whose characteristics are detailed in the [[List_of_Nuclear_Magnetic_Resonance_experiments|List of NMR experiments]]. | |||
[[Image:COSY.png|right|thumb|250px|<br/> | This 2-D COSY spectrum shows two diagonal peaks and two cross peaks. The observed cross peaks are used to identify (correlate) the chemical shifts of nuclei that are J-coupled. ]] | [[Image:COSY.png|right|thumb|250px|<br/> | This 2-D COSY spectrum shows two diagonal peaks and two cross peaks. The observed cross peaks are used to identify (correlate) the chemical shifts of nuclei that are J-coupled. ]] | ||
'''Two dimensional correlation spectroscopy''' <ref | '''Two dimensional correlation spectroscopy''' <ref name=Aue1976/> <ref>U.Piantini, O.W.Sorensen and R.R.Ernst. (1982). J.Am.Chem.Soc. 104, 6800.</ref>(2D-COSY): Correlates chemical shifts of J-coupled nuclei. | ||
'''Two dimensional nuclear overhauser effect spectroscopy'''<ref>J.Jeener, B.H.Meier, P.Bachmann and R.R.Ernst. (1979). J.Chem.Phys. 71, 4546.</ref> (2D-NOESY): correlates chemical shifts of nuclei that exhibit significant [[Nuclear_overhauser_effect | Nuclear Overhauser effect]]<ref>A.W.Overhauser. (1953). Phys. Rev. 92, 411.</ref>. For molecules that experience free rotation along all three dimensions, the Nuclear Overhauser effect is generally observable between nuclei that are less than 5 angstroms apart. | '''Two dimensional nuclear overhauser effect spectroscopy'''<ref>J.Jeener, B.H.Meier, P.Bachmann and R.R.Ernst. (1979). J.Chem.Phys. 71, 4546.</ref> (2D-NOESY): correlates chemical shifts of nuclei that exhibit significant [[Nuclear_overhauser_effect | Nuclear Overhauser effect]]<ref>A.W.Overhauser. (1953). Phys. Rev. 92, 411.</ref>. For molecules that experience free rotation along all three dimensions, the Nuclear Overhauser effect is generally observable between nuclei that are less than 5 angstroms apart. | ||
==Biomolecular NMR spectroscopy== | ==Applications of NMR spectroscopy== | ||
===Biomolecular structure determination=== | |||
NMR spectroscopy can be used to determine the [[Protein_structure|structure of macromolecules]]<ref>K. Wüthrich, NMR of Proteins and Nucleic Acids, Wiley Interscience, New York, 1986.</ref> and to obtain information regarding their dynamics<ref>Z.L. Mádi, C. Griesinger, and R.R. Ernst, J. Am. Chem. Soc. 112, 2908 (1990).</ref>. However, the NMR spectra of macromolecules are much more complicated than those of small molecules and it is usually necessary to use multidimensional NMR spectroscopy to obtain data that can be used for structural analysis. The equential resonance assignment method was developed in order to associate specific nuclei in a protein with the observed resonance frequencies<ref>A. Dubs, G. Wagner and K. Wüthrich. (1979) Biochim. Biophys. Acta 577, 177.</ref>. <ref>G. Wagner and K. Wüthrich (1982) J. Mol. Biol. 155, 347</ref>Subsequently, the information obtained from quantitative and qualitative analysis of nuclear Overhauser effects, J-coupling<ref>A. Pardi, M. Billeter and K. Wüthrich. (1984) J. Mol. Biol. 180, 741</ref> and chemical shifts is converted into geometric restraints. These geometric restraints are then subsequently used to build a model of the molecule<ref name=Braun1981>{{citation | |||
| last1 = Braun | first1 = Werner | |||
| last2 = Bösch | first2 = Chris | |||
| last3 = Brown | first4 = Larry R. | |||
| last4 = Gō | first4 = Nobuhiro | |||
| last5 = Wüthrich | first5 = Kurt | |||
| year = 1981 | |||
| title = Combined use of proton-proton overhauser enhancements and a distance geometry algorithm for determination of polypeptide conformations. Application to micelle-bound glucagon | |||
| journal = Biochimica et Biophysica Acta (BBA) - Protein Structure | |||
| volume = 667 | |||
| pages = 377-396 | |||
| doi = 10.1016/0005-2795(81)90205-1 | |||
| url = http://dx.doi.org/10.1016/0005-2795(81)90205-1 | |||
}}</ref><ref>Havel, T.F. and Wüthrich, K. (1984) Bull. Math. Biol. 46, 673</ref>. | |||
NMR spectroscopy | ===Drug design and development=== | ||
NMR spectroscopy is a useful tool in drug design and development. At present, the most extensive application of NMR spectroscopy is for structure determination of ligands and receptors. In addition, NMR spectroscopic methods are used to study the interactions of ligands with receptors<ref> Diercks, Coles and Kessler. Current Opinion in Chemical Biology. (2001), 5, 285-291</ref><ref> Fernandez and W.Jahnke. Drug Discovery Today. (2004) 1, 277-283</ref> even when the binding is weak and transient<ref>J. W. Peng,J. Moore and N. Abdul-Manan. Progress in NMR spectroscopy. (2004) 44, 225-256</ref> <ref>M. Coles, M. Heller and H. Kessler. Drug discovery today. (2003). 8, 803-810 </ref>; and to build structure activity relationships.<ref>S.B.Shuker, P.J.Hajduk, R.P.Meadows and S.W.Fesik (1996) Science 274, 1531</ref>. Stable ligand–receptor complexes can be studied by either isotope-edited or isotope-filtered NMR spectroscopy. Either the ligand or the receptor can be labeled with an NMR active stable isotope. In isotope-edited NMR experiments, the spectra of the labeled part of the complex are selectively obtained; whereas in isotope-filtered NMR experiments the spectra of the labeled part of the complex are selectively suppressed to record the signals from the unlabeled components of the complex. 2D-EXSY (Two-dimensional exchange spectroscopy) or transferred-NOe spectroscopy are generally used to study weaker ligand-receptor complexes (intermediate exchange). Weak and transient binding leads to rapid exchange of ligand between the complex and free form (fast exchange on the NMR time scale); even this can be detected by monitoring the changes in the chemical shift of the ligand or the chemical shifts of the residues of the receptor at the active site. A new approach to drug development (labeled SAR by NMR) has been developed based on the ability to detect the weak binding of fragments using NMR spectroscopic chemical shift changes; subsequently the fragments identified to bind weakly at separate sites on the receptor can be joined together using an inert linker and the resulting compound would be expected to bind much more strongly than either fragment (due to entropic and additive enthalpic effects). | |||
NMR spectroscopy of drugs with stable isotope labels may be used to monitor the rate of dissolution of an administered drug, to monitor its absorption, distribution and elimination and also to identify the products into which it is transformed. | |||
MR spectroscopy is of particular use in physiological studies, because the system of interest can be studied in a non-invasive manner, and also because it is possible to quantify the changes in a large set of metabolites simultaneously. [[Metabonomic]] studies characterize the physiological changes by quantifying the entire set of metabolites in an organism or its components; the ability of NMR spectroscopy to provide quantitative information on complex mixtures is of particular use in such studies. | |||
Information regarding spatial distribution of NMR parameters may be obtained by using magnetic field gradients<ref>D.D.Osheroff, W.J.Gully, R.C.Richardson and D.M.Lee, Phys. Rev. Lett. (1972) 29, 920</ref>. This is the basis of [[Magnetic resonance imaging|Magnetic resonance imaging]]<ref>P.C. Lauterbur, (1973) Nature 242, 190 </ref><ref>Anil Kumar, D. Welti, and R.R. Ernst, (1975) J. Magn. Reson. 18, 69 .</ref> <ref>P. Mansfield, A.A. Maudsley, and T. Baines, J. Phys. E9, 271 (1976).</ref> (MRI) a tool that has found extensive applications<ref>W.A. Edelstein, J.M.S. Hutchison, G. Johnson, and T.W. Redpath, (1980) Phys. Med. Biol. 25, 751.</ref> in medical diagnostics. | |||
===Food technology=== | |||
== | |||
NMR spectroscopy, usually in conjunction with other techniques, is useful for qualitative as well as quantitative determination of the constituents of food material. A few examples of application of magnetic resonance techniques in food science/technology are<ref>I. Farhat,P. Webb , G. Belton. Editors, | NMR spectroscopy, usually in conjunction with other techniques, is useful for qualitative as well as quantitative determination of the constituents of food material. A few examples of application of magnetic resonance techniques in food science/technology are<ref>I. Farhat,P. Webb , G. Belton. Editors, | ||
Magnetic Resonance in Food Science: From Molecules to Man. Royal Society of Chemistry (RCS) 2007. </ref>: | Magnetic Resonance in Food Science: From Molecules to Man. Royal Society of Chemistry (RCS) 2007. </ref>: | ||
* NMR spectroscopy has been used to assess the quality of wines. | * NMR spectroscopy has been used to assess the quality of wines. | ||
* Magnetic resonance techniques have been used to monitor the ripening of cheese. In addition, spectroscopic information has been used to determine the time dependence of the degradation of packed cheese. | * Magnetic resonance techniques have been used to monitor the ripening of cheese. In addition, spectroscopic information has been used to determine the time dependence of the degradation of packed cheese. | ||
* Magnetic resonance techniques have been applied to obtain process information in the production of bread. | * Magnetic resonance techniques have been applied to obtain process information in the production of bread. | ||
* Magnetic resonance has been useful to study the time dependence of hydration of starch, which has important consequences for technology of many foods. | * Magnetic resonance has been useful to study the time dependence of hydration/gelatinization of starch grains, which has important consequences for technology of many foods. | ||
* NMR spectroscopy has been used for accurate determination of k-value, which is an indicator of freshness of fish. | * NMR spectroscopy has been used for accurate determination of k-value, which is an indicator of freshness of fish. | ||
In such applications, the ability of NMR spectroscopy to resolve complex mixtures, its non-invasive nature, and its applicability to matter in a wide variety of states is particularly useful. | |||
==Conclusion== | |||
NMR spectroscopy is, arguably, the most powerful analytical technique in terms of the range of systems that can be studied and the nature of information that can be obtained regarding the system of interest. In spite of this, NMR spectroscopy has found a very limited application in industrial applications (other than in research and development). This is due to the fact that conventional NMR spectrometers are expensive, bulky, weigh about a ton, and require an environment that is essentially free from electrical, magnetic, thermal and vibrational noise. These requirements are difficult to satisfy in a typical 'factory'. However, recent developments in [[NMR instrumentation]], such as active shielding of magnets, micro NMR probes and miniaturization of the [[RF electronics]], indicate that smaller, lighter and cheaper NMR spectrometers may be soon be available, at least for specialized applications. Therefore, we expect that NMR spectroscopy will occupy a prominent role in many more industrial applications than at present. | |||
NMR spectroscopy is | |||
==Further reading== | ==Further reading== | ||
Fundamentals of Physics. Halliday, Resnick and Walker. | Fundamentals of Physics. 6th Ed. (2001). D.Halliday, R.Resnick and J.Walker. Wiley. | ||
Biophysical Chemistry. Cantor and Schimmel. | Biophysical Chemistry. Vol.II. (1980) C.R.Cantor and P.R.Schimmel. Freeman | ||
Principles of Nuclear Magnetic Resonance spectroscopy in one and two dimensions. (1987). R.R.Ernst, G. Bodenhausen and A.Wokaun. Clarendon Press. Oxford. | Principles of Nuclear Magnetic Resonance spectroscopy in one and two dimensions. (1987). R.R.Ernst, G. Bodenhausen and A.Wokaun. Clarendon Press. Oxford. | ||
NMR of proteins and nucleic acids. K.Wuthrich. Wiley. | NMR of proteins and nucleic acids. (1986). K.Wuthrich. Wiley. | ||
Quantum description of high resolution NMR in liquids. M.Goldman. Oxford. | Quantum description of high-resolution NMR in liquids. (1988) M.Goldman. Oxford. | ||
Principles of Magnetic Resonance (1996) Charles P. Slichter. Springer Series in Solid-State Sciences. | Principles of Magnetic Resonance (1996) Charles P. Slichter. Springer Series in Solid-State Sciences. | ||
[http://www.amazon.com/Protein-NMR-Spectroscopy-Principles-Practice/dp/012164491X/ref=pd_sim_b_title_2 Protein NMR spectroscopy: Principles and Practice. (2006) J.Cavanagh, W.J. Fairbrother, A6G. Palmer, N.J. Skelton, M.Rance. Academic Press. ] | [http://www.amazon.com/Protein-NMR-Spectroscopy-Principles-Practice/dp/012164491X/ref=pd_sim_b_title_2 Protein NMR spectroscopy: Principles and Practice. (2006) J.Cavanagh, W.J. Fairbrother, A6G. Palmer, N.J. Skelton, M.Rance. Academic Press. ] | ||
[http://www.amazon.com/Understanding-NMR-Spectroscopy-James-Keeler/dp/0470017872/ref=sr_1_1?ie=UTF8&s=books&qid=1200437887&sr=1-1 Understanding NMR spectroscopy. (2005) J.Keeler. Wiley] | [http://www.amazon.com/Understanding-NMR-Spectroscopy-James-Keeler/dp/0470017872/ref=sr_1_1?ie=UTF8&s=books&qid=1200437887&sr=1-1 Understanding NMR spectroscopy. (2005) J.Keeler. Wiley] | ||
[http://www.amazon.com/Spectrometric-Identification-Organic-Compounds-Silverstein/dp/0471393622/ref=sr_1_3?ie=UTF8&s=books&qid=1200437776&sr=1-3 Spectrometric Identification of Organic Compounds. (2005) Robert M. Silverstein, Francis X. Webster, and David Kiemle.] | [http://www.amazon.com/Spectrometric-Identification-Organic-Compounds-Silverstein/dp/0471393622/ref=sr_1_3?ie=UTF8&s=books&qid=1200437776&sr=1-3 Spectrometric Identification of Organic Compounds. (2005) Robert M. Silverstein, Francis X. Webster, and David Kiemle.] | ||
BioNMR in Drug Research. (2006) O.Zerbe, R.Mannhold, H.Kubinyi and G.Folkers. Wiley-VCH. | |||
[http://www.amazon.com/NMR-Drug-Design-Analytical-Biotechnology/dp/0849378249/ref=sr_1_31?ie=UTF8&s=books&qid=1200437347&sr=1-31 NMR in Drug Design. David J. Craik. (1995). Crc Series in Analytical Biotechnology.] | [http://www.amazon.com/NMR-Drug-Design-Analytical-Biotechnology/dp/0849378249/ref=sr_1_31?ie=UTF8&s=books&qid=1200437347&sr=1-31 NMR in Drug Design. David J. Craik. (1995). Crc Series in Analytical Biotechnology.] | ||
==References== | ==References== | ||
{{reflist|2}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 06:01, 23 September 2024
NMR spectroscopy, or nuclear magnetic resonance spectroscopy (also called magnetic resonance spectroscopy, or MRS) is a spectroscopic method that uses the nuclear magnetic resonance principle to manipulate the spin states of atomic nuclei to investigate physical and chemical properties.
Samples that are typically studied range from single atoms, molecules, molecular clusters, proteins, nucleic acids, micelles and nanoparticles, up to objects as large as humans (see also MRI). It manipulates the distribution of energy states by exciting the atoms with electromagnetic radiation that is proportional to both the applied magnetic field and the magnetogyric ratio of the isotope studied, and observing the electromagnetic signals emitted as the high energy states relax back to an equilibrium state. Thus, it does not measure actual atomic energy levels, but instead measures the energy differences between spin states of magnetically active nuclei in the presence of a magnetic field by using radio frequency electromagnetic radiation.[1][2] [3] The energy differences between the spin states of the nuclei depend upon the nature of the atom and are influenced by its environment. However, NMR spectroscopy is not limited to the measurement of energy differences between the spin states, because NMR signals are also influenced by the local motion of the nucleus, the rotational motion of the molecule within which the observed nucleus resides, chemical exchange reactions, and neighboring molecules. Therefore, NMR spectroscopy provides static information, such as global structure, stereochemistry, and composition, as well as dynamic information such as protein folding/unfolding equilibria, chemical exchange rates, molecule diffusion or rotation rates. NMR technology is used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI).
Pulses of radio-frequency electromagnetic radiation can be used to perturb the nuclear spin systems in a variety of ways; the time-dependent response of the system of interest can be recorded and analyzed:
- to correlate different spectral properties of nuclei and/or
- to extract information regarding interactions between nuclear spins within the same molecule and/or
- to obtain information regarding intermolecular interactions.
The amplitude, frequency, phase, and duration of pulses of radio-frequency electromagnetic radiation, as well as static and dynamic position-dependent magnetic fields, can be varied in many combinations, giving rise to a wide variety of NMR spectroscopic experiments.
NMR spectroscopic techniques are used extensively for structural elucidation of natural products and for quantitative analysis of components of complex mixtures such as body fluids. However, applications are not limited to these systems; and NMR spectroscopy has been used for the study of matter in disordered, ordered, and partially ordered systems such as gases, liquids, quantum fluids [4] [5], superconductors, solutions, amorphous solids, crystalline solids, liquid crystals, membranes and living organisms. NMR spectroscopic methods have also found use in quantum computing.
NMR spectroscopy: Observable parameters
The chemical shift
The nuclei in molecules are surrounded by electrons. The applied magnetic field induces a circulation of electrons, which in turn produces an additional magnetic field. This effect is called 'shielding', because the magnetic field induced by the circulation of charge is in opposite direction to the field (external) that was responsible for the circulation of charge. Therefore, the nuclei in a given molecule are subjected to a net magnetic field which is the sum of the applied magnetic field and the induced magnetic field.
where is a tensor; however, for molecules rotating rapidly in all directions, such as molecules in a gas, liquid, or solution, can be approximated by a scalar and is known as the shielding constant.
depends upon the electron density as well as polarizability, which vary substantially depending upon the nature of the molecule and the location within the molecule. As a consequence, for a given value of the applied field, nuclei in different molecules and even nuclei in different parts of the same molecule may encounter different net values of the magnetic field. This results in a variation in the resonance frequency.
where is the resonance frequency for the nucleus labeled i, is the net magnetic field at nucleus i, and is the magnetogyric ratio of the isotope of interest.
The relative change in the resonance frequency is called the chemical shift[6][7][8][9].
- (ppm)
where is the resonance frequency of a standard. The chemical shift is generally quoted in ppm. The ppm scale is used because ppm values are field-independent, thus giving the same results on different magnets, and because comparing (field-dependent) numbers like 900.000000003 vs 899.9999997 MHz is inconvenient. As these small changes indicate, the magnetic fields utilized in high-resolution NMR must be constant within parts per billion.
For proton NMR spectroscopy of organic compounds, tetramethylsilane(TMS) was chosen as the reference. It is often used as an internal standard. However, TMS has low solubility in aqueous solution; therefore, it is often necessary to use a secondary standard such as DSP.
The chemical shifts of functional groups in many molecules have been measured, and they provide a basis for identification of functional groups in novel molecules.
Signal area
The area of a signal is proportional to the total number of contributing nuclei. For example, in the 1H NMR spectrum of a pure compound containing a single methyl group and a single methylene group, the relative areas of the corresponding signals will be in the ratio 3:2, because there are 3 protons in the methyl group and 2 in the methylene group.
If the pure compound can exist in multiple conformations, and if the transitions between the different conformational states occur on a time scale that is slow with reference to the relevant NMR time scale (typically milliseconds), then it may be possible to observe separate signals corresponding to the different conformations in the NMR spectrum. In such a case, the relative areas of the signals corresponding to different conformations will be proportional to the fractions of the molecules that exist in each conformational state during the time that the NMR spectrum was acquired.
Many small molecules can exist in multiple conformations due to rotation about single bonds, however, such rotation is generally rapid at room temperature and hence separate signals are usually not observed for the different rotational isomers that exist at equilibrium. For large molecules, e.g., proteins, the close packing of the constituent amino acids results in restricted rotation about many single bonds and complete loss of conformational freedom for many other single bonds. Such restricted rotation about single bonds results in separate NMR signal for each conformer, and the areas of the NMR signals are again proportional to the populations of the conformers.
In the NMR spectra of mixtures, the relative areas of signals can be used to deduce information regarding the relative concentration of each compound. The very high resolution of NMR spectra enables us to resolve a very large number of compounds, and hence determine the relative concentrations of a large number of chemical species. This is of particular use in vivo spectroscopy and NMR-based metabolomics studies in which blood plasma or serum, urine, cerebral spinal fluid, or tissue extracts can be studied for metabolic disorders or chemical injury. The ability to resolve the signals of a large number of chemicals/biochemicals can be enhanced significantly by using 2D NMR, but often using methods like targeted profiling, statistical analysis, principal components analysis and other techniques can be used to identify many substances.
Systems undergoing physical and chemical changes can also be monitored by NMR spectroscopy as the interconverting species usually have different chemical shifts. The changes in the relative areas of the reactants and products can be used to obtain information regarding the time course of the reaction. This is possible if the time scale of the conversion is slow with respect to the NMR time scale. Systems which interconvert very fast compared to the NMR data acquisition time are observed as a single, averaged single entity, while those exchanging at about the same time frame can be broadened out so that no (direct) signal is observed.
J-coupling and multiplicity
J-coupling, also known as scalar coupling, causes splitting of NMR signals due to the interactions between different nuclei in the same molecule that are mediated through electrons in chemical bonds[10][11][12]. Usually, the J-coupling interaction is observable between nuclei that are separated from each other by three or fewer bonds. If the coupling is weak the resulting pattern is a function of the number of neighboring nuclei, and this information plays a critical role in structural elucidation of small organic molecules. In addition, the magnitude of the line-splitting (coupling constant) provides information regarding the molecular conformation.
For weak coupling, the multiplicity of a signal is expected to be 2nI + 1 where n is the number of nuclei with spin angular momentum quantum number (spin) I that have J coupling with the nucleus responsible for the signal being observed. If all magnetically active nuclei are protons, then the multiplicity is equal to n + 1, because I = 1/2 for protons. In addition, the relative intensities of the peaks within a multiplet is given by the coefficients of the binomial expansion. This is known as the n + 1 rule. In using the n + 1 rule, couplings between magnetically equivalent nuclei are not considered because the effects of J-coupling are not observable in a normal 1D NMR spectrum if the nuclei involved in the interaction are magnetically equivalent. For example, in the fragment CH3-CH2-O-, the signal corresponding to the methyl (CH3) protons will have a multiplicity of three, because each of the methyl hydrogen has a J-coupling to each of the two (equivalent) methylene (CH2) protons, hence n = 2, I = 1/2, and 2nI + 1 = 3. The signal corresponding to the methylene group of protons will be a quartet, as each methylene proton is expected to have J coupling to each of the three methyl (CH3) protons, hence n = 3, I = 1/2, and 2nI + 1 = 4. In this case, the pairs of nuclei that have observable J-coupling are separated by three bonds. Note that interactions between magnetically equivalent nuclei, such as interactions between the different protons of the same methyl group (separated by only two bonds), need not be considered when predicting the multiplicity. In this example the three protons in the methyl group are treated as magnetically equivalent and the two protons in the methylene group are treated as magnetically equivalent by assuming that free rotation occurs about the single bond separating the methyl and methylene groups. If this is not the case, e.g., if restricted rotation occurs about the single bond and if the fragment is placed in an asymmetric environment (such as part of a rigid macromolecule), then the methylene protons may no longer be assumed to be magnetically equivalent.
The 2nI + 1 rule assumes that all of the neighboring geminal nuclei (i.e., those with observable J-coupling to nucleus being observed) are equivalent. If this is not the case, then the multiplet structure can still be predicted by considering first the coupling to one set of equivalent J-coupled nuclei and predicting that the effect of the remaining nuclei will cause additional splitting of the multiplet generated by interaction with the first set.
The magnitude of the J-coupling depends on the number of bonds separating the interacting nuclei as well as on the geometry. For 3J coupling, i.e., coupling between nuclei separated by three bonds, the magnitude of the coupling between the interacting nuclei is given by the Karplus equation
where θ is the dihedral angle involving the nuclei of interest. The values of A,B and C depend on the chemical nature of the fragment. The Karplus equation is useful for conformational analysis of molecules, particularly biopolymers such as polypeptides[13] and nucleic acids. The parameters A,B and C of the Karplus equation have been determined for most combinations of nuclei that occur in organic compounds, by comparing experimental NMR and X-ray crystallographic data. If relevant experiment data is not available, the magnitude of the J coupling may be calculated by using quantum chemical calculations[14]; however the prediction accuracy of ab initio calculations is often lower than that obtained from empirical parametrization.
The net magnetization vector
In the presence of an external magnetic field B, the distribution of the number of nuclei in the different allowed nuclear spin states follows the Boltzmann distribution at equilibrium. i.e. for a two state system with states and
where
- number of nuclei in state ; number of nuclei in state
- Energy of state ; Energy of state
- T = Absolute temperature in Kelvin; k = Boltzmann constant
If the energy of state is greater than that of state , then fewer nuclei will be present in the higher energy state . However, since the energy difference between these two states is small the population difference is quite small and the macroscopically observable net magnetization vector for the entire population will be the vectorial sum of the magnetic moments of all the nuclei present in the sample. At equilibrium, in a homogeneous magnetic field, although the orientation of the spin magnetic moments of individual nuclei is restricted to certain directions with respect to the applied magnetic field (which usually defines the z axis), there is no preference for any direction for the projection of the magnetic moment onto the x-y plane. The X- and Y-components of the net magnetization vector of the sample should be zero at equilibrium because the X- and Y-components of the spin magnetic moments of individual nuclei are randomly oriented and the net magnetization vector is the vectorial sum of the spin magnetic moments of individual nuclei. Therefore, the equilibrium magnetization will be
where
- N = total number of nuclei in sample; Magnetization vector (net) at equilibrium
- energy of state i; z-component of magnetic moment of state i
- degeneracy of state i
For a two-state system, the are equal in magnitude but opposite in direction. However, there are more nuclei in the lower energy state at the temperature of the experiment T, hence the numerator in the sum above is nonzero. Therefore, at equilibrium, the net magnetization vector has only one non-zero component (the -component) when the system is placed in a static homogeneous magnetic field.
In the presence of homogeneous magnetic field (possibly time dependent), represented by the vector B, the magnetization vector experiences a torque and the time dependence of the net magnetization vector M (neglecting relaxation effects) is
The Bloch equations describe the time dependence of the different components of the net magnetization vector subject to relaxation, in the presence of a time-dependent magnetic field.
Relaxation time
After a collection of nuclei in a magnetic field that is at equilibrium with its surroundings is perturbed in some manner (usually by a pulse of electromagnetic radiation), the system requires a certain amount of the time to return to equilibrium. If this process is exponential, the rate constant is called relaxation rate. The relaxation rate is inversely proportional to relaxation time[15] [16] [17]. T1 relaxation time characterizes the return to equilibrium of the longitudinal component of the magnetization of the collection of nuclei. Similarly, T2 relaxation time characterizes the return to equilibrium of the transverse component of the magnetization of the collection of nuclei that are being studied. In a static homogeneous magnetic field, the transverse component of the net magnetization vector for a sufficiently large collection of nuclei is always zero, at equilibrium.
The dominant mechanism of relaxation is usually the dipolar interaction with the closest neighbor. For a pair of identical spins separated by a distance , in a homogeneous magnetic field, undergoing isotropic rotational motion in solution, the relaxation rates are:
- where is the spectral density function
- is the mean time required for rotational motion of the pair of nuclei by one radian
- is the magnetic permeability of free space
- is the gyromagnetic ratio and
- is the Planck's constant divided by .
For a pair of nonidentical spins I and S, separated by a distance r, the time dependence of the expectation values of the z-components of magnetization are given by the Solomon equations:
and are the auto- and cross relaxation rates, respectively. and is responsible for the Nuclear overhauser effect.
A homogeneous magnetic field, isotropic rotational motion, and negligible chemical shift anisotropy are assumed in the derivation of the equations described above.
Dipolar coupling and nuclear Overhauser effect
Irradiation at the resonance frequency of one nucleus in the molecule may cause changes in the intensity of a signal at a different frequency corresponding to another nucleus—this is called the nuclear Overhauser effect[18] (Noe). The nuclear Overhauser effect is due to dipole–dipole interactions between the magnetic moments of a pair of nuclei. Unlike J-coupling, this interaction is not mediated through bonds. Hence, it may be possible to observe the nuclear Overhauser effect between pairs of nuclei separated by many bonds, provided that they are in spatial proximity. The strength of the observable nuclear Overhauser effect for molecules in solution is proportional to the inverse of the sixth power of the distance between the two nuclei due to averaging caused by rotational motion. Both the magnitude as well as the sign of the nuclear Overhauser effect depend on the rotational frequencies of the pair of nuclei with respect to the applied magnetic field. The Noe enhancement, , in the steady state, when the resonance frequency of spin I is irradiated and the intensity of spin S is monitored is = ( I )/ (S S). This indicates that considerable enhancement in the intensity of the S signal can be obtained by irradiation at the frequency of the I spin, provided that I/S is greater than 1, because /S is approximately 1/2 when w is much smaller than 1 .
However, when w is much greater than 1, /S approaches –1 and negative Noe enhancements are obtained.
The sign of changes from positive to negative when w is close to 1 and under such conditions the Noe effect may not be observable. This happens for rigid molecules with relative molecular mass about 500 at room temperature, e.g., many hexapeptides.
For most molecules (in isotropic media, at room temperature), direct observation of dipolar coupling in solution NMR spectra (as a separation of the components of a signal) is not possible, because dipolar interactions are averaged over all orientations of the molecule. However, it is possible to obtain partial alignment of macromolecules using anisotropic media, leading to incomplete averaging of the dipolar interactions. In such cases there is an 'apparent' change in the measured values of J-coupling constants because the residual dipolar coupling has the same form as the weak scalar coupling Hamiltonian. For a pair of nuclei, at a fixed distance, the magnitude and signs of the residual dipolar couplings are angle dependent. Hence, measurements of residual dipolar couplings (RDC) can be used to obtain angular constraints (used for structure determination).
Instrumentation
A typical NMR spectrometer contains three components: (1) magnet (2) probe (3) RF electronics.
For any system at equilibrium in the absence of a magnetic field, all the nuclear spin states are equally populated and hence there is no net polarization due to the nuclear spins. Therefore, it is necessary to introduce an external magnetic field which leads to preferential population of the lower energy nuclear spin states. The energy differences between the different nuclear spin states are proportional to the strength of the magnetic field. Therefore, higher magnetic fields lead to greater separation between the energy levels and greater polarization at equilibrium. The required magnetic field is usually provided by an external magnet.
High magnetic fields (1–17 tesla) are generally preferred for high resolution, high sensitivity NMR spectroscopic experiments. In general, higher magnetic fields provide higher signal-to-noise ratio as well as higher resolution. Most high resolution NMR spectrometers used by chemists and biologists use superconducting magnets. However, NMR spectrometers with lower resolution may use permanent magnets or electromagnets. It is also feasible to carry out certain types of NMR experiments in much weaker fields—in fact many NMR spectroscopic experiments have been conducted using the earth's magnetic field.
The probe in an NMR spectrometer is responsible for coupling the radio frequency electromagnetic field generated by the RF electronics to the sample. It is also responsible for detecting the NMR signal (through induction) and passing it to the receiver.
RF electronics consists of two basic subsystems: The transmitter and the receiver subsystems.
Transmitter subsystem: The transmitter subsystem is responsible for generating a radio frequency signal in the form of a sequence of pulses with specified frequency, amplitude, phase, and duration for each pulse. It consists of the RF synthesizers and amplifiers. This subsystem is responsible for generating waveforms of the required frequency, amplitude, phase, and duration at specified times. Multiple RF synthesizers are required because many MR experiments require simultaneous application of RF pulses of different frequency. Earlier MR systems used waveform generators with subsequent phase modulation. However, more recent systems rely on DDS (direct digital synthesis).
RF switch is responsible for coupling either the Transmitter or the Receiver subsystem to the probe. This ensures that the sensitive receiver subsystem is not overloaded with the high-powered RF signal generated by the transmitter system. Also, the receiver is 'blanked' during the transmission and for a short duration afterward.
Receiver subsystem: The receiver subsystem is responsible for amplification of the NMR signal and for its conversion to a lower frequency so that the signal can be digitized. This consists of the components: preamplifier, amplifier, demodulator, and the analog-to-digital converter (ADC). The demodulator is responsible for subtracting a reference frequency of specified phase from the observed signal.
Magnetic field gradients of specified strength and duration are generated by passing current through coils of appropriate geometry. Magnetic field gradients are controlled by an independent subsystem.
Shimming is the process that corrects for spatial inhomogeneities in the magnetic field.
Field frequency lock is used to keep the magnetic field fixed at a specified value during the duration of the experiment.
Pulsed (radio frequency) NMR spectroscopy
Spin echoes
A pulse of radio frequency (RF) radiation is applied for sufficient duration to tip the net magnetization vector into the x–y plane; this is followed by a short delay , followed by another RF pulse that inverts the magnetization around the x-axis, followed by another short delay . The magnetization at the end of this pulse-sequence is
The transverse relaxation time can be measured by repeating the experiment with different value of , and plotting vs . The resulting plot is expected to be a straight line with slope .
If the above experiment is carried out with a magnetic field gradient during the two delays then
where D is the diffusion coefficient and G is the magnetic field gradient. Repeating this experiment with different values of G enables us to measure the diffusion coefficient D.
Fourier transform NMR spectroscopy
Fourier transform NMR spectroscopy (Ernst [19][20]) is performed in the following way: A pulse (or a pulse train) of electromagnetic radiation is used to cause a perturbation in the system. The time-dependent response of the system is recorded (this time-dependent response is often referred to as the free induction decay, abbreviated as fid). A fourier transform of the response gives information regarding the frequency response. In the case of a single pulse perturbation, the fourier transform of the time-dependent response is equivalent to a 1D NMR spectrum.
| fid | NMR spectrum | |
|---|---|---|
| FT{FID} → spectrum. |
Multidimensional NMR spectroscopy
Multidimensional NMR spectroscopy (nD NMR; Jeener [21]; Aue et al.[22]) The nuclei in a magnetic field are subjected to a series of pulses of electromagnetic radiation separated by delays. The time-dependent response of the system is recorded. The delays between the pulses may be fixed or incremented systematically between different repetitions of the experiment. The number of variable delays determines the dimensionality of the experiment. A multidimensional Fourier Transform of the entire data set characterizes the frequency responses of the system and enables a correlation between different NMR parameters. Different combinations of the pulses and delays known as 'pulse sequences' enable us to correlate and measure different types of NMR parameters. Some common examples of multidimensional NMR spectroscopy experiments (2D, 3D and 4D) include: COSY, NOESY, TOCSY, EXSY, HSQC, HNHA, HSQC-NOESY, HNCA, HNCO, HNCACO, HSQC-NOESY-HSQC whose characteristics are detailed in the List of NMR experiments.
Two dimensional correlation spectroscopy [22] [23](2D-COSY): Correlates chemical shifts of J-coupled nuclei.
Two dimensional nuclear overhauser effect spectroscopy[24] (2D-NOESY): correlates chemical shifts of nuclei that exhibit significant Nuclear Overhauser effect[25]. For molecules that experience free rotation along all three dimensions, the Nuclear Overhauser effect is generally observable between nuclei that are less than 5 angstroms apart.
Applications of NMR spectroscopy
Biomolecular structure determination
NMR spectroscopy can be used to determine the structure of macromolecules[26] and to obtain information regarding their dynamics[27]. However, the NMR spectra of macromolecules are much more complicated than those of small molecules and it is usually necessary to use multidimensional NMR spectroscopy to obtain data that can be used for structural analysis. The equential resonance assignment method was developed in order to associate specific nuclei in a protein with the observed resonance frequencies[28]. [29]Subsequently, the information obtained from quantitative and qualitative analysis of nuclear Overhauser effects, J-coupling[30] and chemical shifts is converted into geometric restraints. These geometric restraints are then subsequently used to build a model of the molecule[31][32].
Drug design and development
NMR spectroscopy is a useful tool in drug design and development. At present, the most extensive application of NMR spectroscopy is for structure determination of ligands and receptors. In addition, NMR spectroscopic methods are used to study the interactions of ligands with receptors[33][34] even when the binding is weak and transient[35] [36]; and to build structure activity relationships.[37]. Stable ligand–receptor complexes can be studied by either isotope-edited or isotope-filtered NMR spectroscopy. Either the ligand or the receptor can be labeled with an NMR active stable isotope. In isotope-edited NMR experiments, the spectra of the labeled part of the complex are selectively obtained; whereas in isotope-filtered NMR experiments the spectra of the labeled part of the complex are selectively suppressed to record the signals from the unlabeled components of the complex. 2D-EXSY (Two-dimensional exchange spectroscopy) or transferred-NOe spectroscopy are generally used to study weaker ligand-receptor complexes (intermediate exchange). Weak and transient binding leads to rapid exchange of ligand between the complex and free form (fast exchange on the NMR time scale); even this can be detected by monitoring the changes in the chemical shift of the ligand or the chemical shifts of the residues of the receptor at the active site. A new approach to drug development (labeled SAR by NMR) has been developed based on the ability to detect the weak binding of fragments using NMR spectroscopic chemical shift changes; subsequently the fragments identified to bind weakly at separate sites on the receptor can be joined together using an inert linker and the resulting compound would be expected to bind much more strongly than either fragment (due to entropic and additive enthalpic effects).
NMR spectroscopy of drugs with stable isotope labels may be used to monitor the rate of dissolution of an administered drug, to monitor its absorption, distribution and elimination and also to identify the products into which it is transformed.
MR spectroscopy is of particular use in physiological studies, because the system of interest can be studied in a non-invasive manner, and also because it is possible to quantify the changes in a large set of metabolites simultaneously. Metabonomic studies characterize the physiological changes by quantifying the entire set of metabolites in an organism or its components; the ability of NMR spectroscopy to provide quantitative information on complex mixtures is of particular use in such studies.
Information regarding spatial distribution of NMR parameters may be obtained by using magnetic field gradients[38]. This is the basis of Magnetic resonance imaging[39][40] [41] (MRI) a tool that has found extensive applications[42] in medical diagnostics.
Food technology
NMR spectroscopy, usually in conjunction with other techniques, is useful for qualitative as well as quantitative determination of the constituents of food material. A few examples of application of magnetic resonance techniques in food science/technology are[43]:
- NMR spectroscopy has been used to assess the quality of wines.
- Magnetic resonance techniques have been used to monitor the ripening of cheese. In addition, spectroscopic information has been used to determine the time dependence of the degradation of packed cheese.
- Magnetic resonance techniques have been applied to obtain process information in the production of bread.
- Magnetic resonance has been useful to study the time dependence of hydration/gelatinization of starch grains, which has important consequences for technology of many foods.
- NMR spectroscopy has been used for accurate determination of k-value, which is an indicator of freshness of fish.
In such applications, the ability of NMR spectroscopy to resolve complex mixtures, its non-invasive nature, and its applicability to matter in a wide variety of states is particularly useful.
Conclusion
NMR spectroscopy is, arguably, the most powerful analytical technique in terms of the range of systems that can be studied and the nature of information that can be obtained regarding the system of interest. In spite of this, NMR spectroscopy has found a very limited application in industrial applications (other than in research and development). This is due to the fact that conventional NMR spectrometers are expensive, bulky, weigh about a ton, and require an environment that is essentially free from electrical, magnetic, thermal and vibrational noise. These requirements are difficult to satisfy in a typical 'factory'. However, recent developments in NMR instrumentation, such as active shielding of magnets, micro NMR probes and miniaturization of the RF electronics, indicate that smaller, lighter and cheaper NMR spectrometers may be soon be available, at least for specialized applications. Therefore, we expect that NMR spectroscopy will occupy a prominent role in many more industrial applications than at present.
Further reading
Fundamentals of Physics. 6th Ed. (2001). D.Halliday, R.Resnick and J.Walker. Wiley.
Biophysical Chemistry. Vol.II. (1980) C.R.Cantor and P.R.Schimmel. Freeman
Principles of Nuclear Magnetic Resonance spectroscopy in one and two dimensions. (1987). R.R.Ernst, G. Bodenhausen and A.Wokaun. Clarendon Press. Oxford.
NMR of proteins and nucleic acids. (1986). K.Wuthrich. Wiley.
Quantum description of high-resolution NMR in liquids. (1988) M.Goldman. Oxford.
Principles of Magnetic Resonance (1996) Charles P. Slichter. Springer Series in Solid-State Sciences.
Understanding NMR spectroscopy. (2005) J.Keeler. Wiley
BioNMR in Drug Research. (2006) O.Zerbe, R.Mannhold, H.Kubinyi and G.Folkers. Wiley-VCH.
NMR in Drug Design. David J. Craik. (1995). Crc Series in Analytical Biotechnology.
References
- ↑ I. I. Rabi.(1937) Phys. Rev., 51 652
- ↑ N. Bloembergen, E. Purcell and R.V.Pound. (1948). Phys. Rev. 73, 679.
- ↑ F. Bloch, W. Hansen, and M.E. Packard, (1946) Phys. Rev. 69, 127.
- ↑ D.D.Osheroff, W.J.Gully, R.C.Richardson and D.M.Lee, Phys. Rev. Lett. (1972) 29, 920
- ↑ http://nobelprize.org/nobel_prizes/physics/laureates/1996/lee-lecture.pdf
- ↑ W.G. Proctor, F.C. Yu (1950) Phys.Rev. 77, 717.
- ↑ W.C.Dickinson. (1950) Phys. Rev. 77, 736.
- ↑ N.F.Ramsey. (1950) Phys. Rev. 78, 699.
- ↑ N.F.Ramsey. (1952) Phys. Rev. 86, 243.
- ↑ H.S.Gutowsky, D.W.McCall, C.P.Slichter (1951) Phys. Rev. 84, 589.
- ↑ N.F.Ramsey. (1953) Phys. Rev. 91, 303.
- ↑ M.Karplus (1963). J. Am. Chem. Soc. 30, 11.
- ↑ V.F.Bystrov. Progress in NMR Spectroscopy, (1976) 10, 41-82
- ↑ H.Fukui. Progress in NMR spectroscopy (1999) 35, 267-294
- ↑ N. Bloembergen, E. Purcell and R.V.Pound. (1948). Phys. Rev. 73, 679.
- ↑ F. Bloch, W. Hansen, and M.E. Packard, (1946) Phys. Rev. 69, 127.
- ↑ I. Solomon. (1955). Phys. Rev. 99, 559.
- ↑ A.W.Overhauser (1953). Phys. Rev. 92, 411
- ↑ R.R.Ernst, Nobel lecture
- ↑ R.R. Ernst and W.A. Anderson, (1966) Rev. Sci. Instrum. 37, 93
- ↑ J. Jeener. (1971). Unpublished lectures at the Ampere International Summer School II, Basko Polje, Yugoslavia.
- ↑ 22.0 22.1 Aue, W. P. (1976), "Two-dimensional spectroscopy. Application to nuclear magnetic resonance", The Journal of Chemical Physics 64: 2229-2246, DOI:10.1063/1.432450
- ↑ U.Piantini, O.W.Sorensen and R.R.Ernst. (1982). J.Am.Chem.Soc. 104, 6800.
- ↑ J.Jeener, B.H.Meier, P.Bachmann and R.R.Ernst. (1979). J.Chem.Phys. 71, 4546.
- ↑ A.W.Overhauser. (1953). Phys. Rev. 92, 411.
- ↑ K. Wüthrich, NMR of Proteins and Nucleic Acids, Wiley Interscience, New York, 1986.
- ↑ Z.L. Mádi, C. Griesinger, and R.R. Ernst, J. Am. Chem. Soc. 112, 2908 (1990).
- ↑ A. Dubs, G. Wagner and K. Wüthrich. (1979) Biochim. Biophys. Acta 577, 177.
- ↑ G. Wagner and K. Wüthrich (1982) J. Mol. Biol. 155, 347
- ↑ A. Pardi, M. Billeter and K. Wüthrich. (1984) J. Mol. Biol. 180, 741
- ↑ Braun, Werner; Chris Bösch & Brown et al. (1981), "Combined use of proton-proton overhauser enhancements and a distance geometry algorithm for determination of polypeptide conformations. Application to micelle-bound glucagon", Biochimica et Biophysica Acta (BBA) - Protein Structure 667: 377-396, DOI:10.1016/0005-2795(81)90205-1
- ↑ Havel, T.F. and Wüthrich, K. (1984) Bull. Math. Biol. 46, 673
- ↑ Diercks, Coles and Kessler. Current Opinion in Chemical Biology. (2001), 5, 285-291
- ↑ Fernandez and W.Jahnke. Drug Discovery Today. (2004) 1, 277-283
- ↑ J. W. Peng,J. Moore and N. Abdul-Manan. Progress in NMR spectroscopy. (2004) 44, 225-256
- ↑ M. Coles, M. Heller and H. Kessler. Drug discovery today. (2003). 8, 803-810
- ↑ S.B.Shuker, P.J.Hajduk, R.P.Meadows and S.W.Fesik (1996) Science 274, 1531
- ↑ D.D.Osheroff, W.J.Gully, R.C.Richardson and D.M.Lee, Phys. Rev. Lett. (1972) 29, 920
- ↑ P.C. Lauterbur, (1973) Nature 242, 190
- ↑ Anil Kumar, D. Welti, and R.R. Ernst, (1975) J. Magn. Reson. 18, 69 .
- ↑ P. Mansfield, A.A. Maudsley, and T. Baines, J. Phys. E9, 271 (1976).
- ↑ W.A. Edelstein, J.M.S. Hutchison, G. Johnson, and T.W. Redpath, (1980) Phys. Med. Biol. 25, 751.
- ↑ I. Farhat,P. Webb , G. Belton. Editors, Magnetic Resonance in Food Science: From Molecules to Man. Royal Society of Chemistry (RCS) 2007.