Modular arithmetic: Difference between revisions
imported>Barry R. Smith mNo edit summary |
mNo edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[mathematics]], '''modular arithmetic''' (also known as '''remainder arithmetic''') is a method for adding and multiplying that arises from the usual [[elementary arithmetic]] of [[whole number|whole numbers]]. In modular arithmetic, a special number called the '''modulus''' (plural: moduli) is chosen, and whole numbers that leave the same remainder when divided by the modulus are considered indistinguishable. When numbers are added or multiplied in modular arithmetic, one does not care about the whole numerical result, but rather only about its remainder upon division by the modulus. The most familiar examples are '''clock arithmetic''' and the rules for manipulating [[odd number|odd]] and [[even number|even]] numbers, which are the arithmetics coming from the moduli 12 and 2 respectively. | In [[mathematics]], '''modular arithmetic''' (also known as '''remainder arithmetic''') is a method for adding and multiplying that arises from the usual [[elementary arithmetic]] of [[whole number|whole numbers]]. In modular arithmetic, a special number called the '''modulus''' (plural: moduli) is chosen, and whole numbers that leave the same remainder when divided by the modulus are considered indistinguishable. When numbers are added or multiplied in modular arithmetic, one does not care about the whole numerical result, but rather only about its [[remainder]] upon [[division (arithmetic)|division]] by the modulus. The most familiar examples are '''clock arithmetic''' and the rules for manipulating [[odd number|odd]] and [[even number|even]] numbers, which are the arithmetics coming from the moduli 12 and 2 respectively. | ||
Modular arithmetic has many more sophisticated applications than telling time. A notable application is as the foundation for some kinds of modern [[cryptography]]. Within pure mathematics, modular arithmetic is of fundamental importance in [[abstract algebra]] and [[number theory]]. | Modular arithmetic has many more sophisticated applications than telling time. A notable application is as the foundation for some kinds of modern [[cryptography]]. Within pure mathematics, modular arithmetic is of fundamental importance in [[abstract algebra]] and [[number theory]]. | ||
| Line 8: | Line 8: | ||
== Parity arithmetic == | == Parity arithmetic == | ||
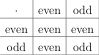
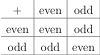
The other example of modular arithmetic familiar to many is the system of rules for adding and multiplying even and odd numbers. These rules describe modular arithmetic when the modulus is two. They can be described through addition and multiplication tables: | |||
[[Image:Mod2mult.jpg|multiplication table modulo two]] [[Image:Mod2add.jpg|addition table modulo two]] | |||
== Modern notation == | == Modern notation == | ||
| Line 13: | Line 17: | ||
The rules and modern notation of modular arithmetic for an arbitrary positive whole number modulus were first introduced by [[Carl Friedrich Gauss|Gauss]] in his foundational work ''[[Disquisitiones Arithmeticae]]'' on number theory (written when he was just 21 years old). | The rules and modern notation of modular arithmetic for an arbitrary positive whole number modulus were first introduced by [[Carl Friedrich Gauss|Gauss]] in his foundational work ''[[Disquisitiones Arithmeticae]]'' on number theory (written when he was just 21 years old). | ||
== Two perspectives: remainders and congruence classes == | == Two perspectives: remainders and congruence classes ==[[Category:Suggestion Bot Tag]] | ||
Latest revision as of 11:00, 20 September 2024
In mathematics, modular arithmetic (also known as remainder arithmetic) is a method for adding and multiplying that arises from the usual elementary arithmetic of whole numbers. In modular arithmetic, a special number called the modulus (plural: moduli) is chosen, and whole numbers that leave the same remainder when divided by the modulus are considered indistinguishable. When numbers are added or multiplied in modular arithmetic, one does not care about the whole numerical result, but rather only about its remainder upon division by the modulus. The most familiar examples are clock arithmetic and the rules for manipulating odd and even numbers, which are the arithmetics coming from the moduli 12 and 2 respectively.
Modular arithmetic has many more sophisticated applications than telling time. A notable application is as the foundation for some kinds of modern cryptography. Within pure mathematics, modular arithmetic is of fundamental importance in abstract algebra and number theory.
Clock arithmetic
Parity arithmetic
The other example of modular arithmetic familiar to many is the system of rules for adding and multiplying even and odd numbers. These rules describe modular arithmetic when the modulus is two. They can be described through addition and multiplication tables:
Modern notation
The rules and modern notation of modular arithmetic for an arbitrary positive whole number modulus were first introduced by Gauss in his foundational work Disquisitiones Arithmeticae on number theory (written when he was just 21 years old).
== Two perspectives: remainders and congruence classes ==