Reflection (geometry): Difference between revisions
imported>Paul Wormer No edit summary |
mNo edit summary |
||
| (10 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[ | In [[Euclidean geometry]], a '''reflection''' is a linear operation σ on <font style="vertical-align: top"><math>\mathbb{R}^3</math></font> with σ<sup>2</sup> = E, the identity map. This property of σ is called ''involution''. An involutory operator is non-singular and σ<sup>−1</sup> = σ. Reflecting twice an arbitrary vector brings back the original vector : | ||
:<math> | :<math> | ||
\sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | \sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | ||
</math> | </math> | ||
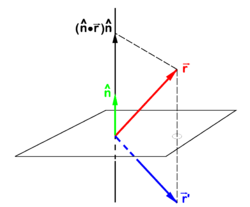
{{Image|Reflection in plane.png|right|250px|The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | The operation σ is an [[isometry]] of <font style="vertical-align: top"><math>\mathbb{R}^3</math></font> onto itself, which means that it preserves inner products and that its inverse is equal to its adjoint, | ||
:<math> | |||
\sigma^\mathrm{T} = \sigma^{-1}\; ( = \sigma). \, | |||
</math> | |||
Hence reflection is also [[symmetric]]: σ<sup>T</sup> = σ. From (det(σ))<sup>2</sup> = det(E) = 1 follows that isometries have [[determinant]] ±1. Those with positive determinant are rotations, while reflections have determinant −1. Because σ is symmetric it has real [[eigenvalue]]s; since the extension of an isometry to a complex space is unitary, its (complex) eigenvalues have modulus 1. It follows that the eigenvalues of σ are ±1. The product of the eigenvalues being its determinant, −1, the sets of eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to −E, minus the identity operator. This operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article. | |||
Sometimes one finds the concept of "reflections in a line", these are rotations over 180°, see [[Rotation matrix#Explicit expression of rotation matrix|rotation matrix]]. | |||
{{Image|Reflection in plane.png|right|250px|Fig. 1. The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | |||
==Reflection in a plane== | ==Reflection in a plane== | ||
If <math>\hat{\mathbf{n}}</math> is a unit vector normal (perpendicular) to a plane—the mirror plane—then <math> (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\hat{\mathbf{n}}</math> is the projection of <math>\vec{\mathbf{r}}</math> on this unit vector. From the figure it is evident that | If <math>\hat{\mathbf{n}}</math> is a unit vector normal (perpendicular) to a plane—the mirror plane—then <math> (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\hat{\mathbf{n}}</math> is the projection of <math>\vec{\mathbf{r}}</math> on this unit vector. From the figure it is evident that | ||
:<math> | :<math> | ||
| Line 19: | Line 28: | ||
\vec{\mathbf{r}}\,' = \vec{\mathbf{r}} - 2 \frac{ (\vec{\mathbf{n}}\cdot\vec{\mathbf{r}})\vec{\mathbf{n}}}{n^2} | \vec{\mathbf{r}}\,' = \vec{\mathbf{r}} - 2 \frac{ (\vec{\mathbf{n}}\cdot\vec{\mathbf{r}})\vec{\mathbf{n}}}{n^2} | ||
</math> | </math> | ||
Sometimes it is convenient to write this as a matrix equation. Introducing the [[dyadic product]], we obtain | |||
:<math> | |||
\vec{\mathbf{r}}\,' = \left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right] \; \vec{\mathbf{r}}, | |||
</math> | |||
where '''E''' is the 3×3 [[identity matrix]]. | |||
Dyadic products satisfy the matrix multiplication rule | |||
:<math> | |||
[\vec{\mathbf{a}}\otimes\vec{\mathbf{b}}]\, [ \vec{\mathbf{c}}\otimes\vec{\mathbf{d}}] = | |||
(\vec{\mathbf{b}} \cdot \vec{\mathbf{c}}) \big( \vec{\mathbf{a}}\otimes\vec{\mathbf{d}} \big). | |||
</math> | |||
By the use of this rule it is easily shown that | |||
:<math> | |||
\left[ \mathbf{E} - \frac{2}{n^2} \vec{\mathbf{n}} \otimes\vec{\mathbf{n}} \right]^2 | |||
= \mathbf{E}, | |||
</math> | |||
which confirms that reflection is involutory. | |||
<!-- | |||
This relation can be immediately generalized to ''m''-dimensional inner product spaces. Let the space ''V''<sub>''m''</sub> allow an orthogonal direct sum decomposition into a 1-dimensional and a (''m''−1)-dimensional subspace, | This relation can be immediately generalized to ''m''-dimensional inner product spaces. Let the space ''V''<sub>''m''</sub> allow an orthogonal direct sum decomposition into a 1-dimensional and a (''m''−1)-dimensional subspace, | ||
:<math> | :<math> | ||
| Line 28: | Line 56: | ||
</math> | </math> | ||
is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | ||
--> | |||
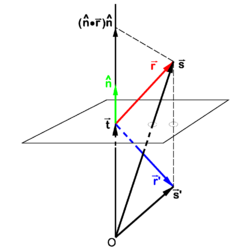
{{Image|Reflection shifted plane.png|left|250px|Fig. 2. The vector <math>\vec{\mathbf{s}}</math> goes to <math>\vec{\mathbf{s}}\,'</math> under reflection}} | |||
==Reflection in a plane not through the origin== | |||
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector <math>\vec{\mathbf{t}}</math>. The length of this vector is the distance from O to the plane. | |||
From Figure 2, we find | |||
:<math> | |||
\vec{\mathbf{r}} = \vec{\mathbf{s}} - \vec{\mathbf{t}}, \quad | |||
\vec{\mathbf{r}}\,' = \vec{\mathbf{s}}\,' - \vec{\mathbf{t}} | |||
</math> | |||
Use of the equation derived earlier gives | |||
:<math> | |||
\vec{\mathbf{s}}\,' - \vec{\mathbf{t}} = \vec{\mathbf{s}} - \vec{\mathbf{t}} | |||
- 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}. | |||
</math> | |||
And hence the equation for the reflected pair of vectors is, | |||
:<math> | |||
\vec{\mathbf{s}}\,' = \vec{\mathbf{s}} | |||
- 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}, | |||
</math> | |||
where <math>\hat{\mathbf{n}}</math> is a unit vector normal to the plane. Obviously <math>\vec{\mathbf{t}}</math> and <math>\hat{\mathbf{n}}</math> are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of <math>\vec{\mathbf{t}}</math>, | |||
:<math> | |||
\vec{\mathbf{s}}\,' = \vec{\mathbf{s}} | |||
- 2 \frac{\vec{\mathbf{t}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})}{t^2}\vec{\mathbf{t}}, \quad | |||
t^2 \equiv \vec{\mathbf{t}}\cdot \vec{\mathbf{t}}. | |||
</math> | |||
==Two consecutive reflections== | |||
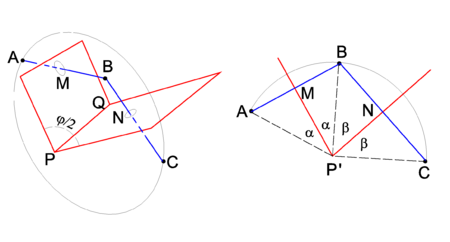
{{Image|Two reflections.png|right|450px|Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′}} | |||
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 3, where PQ is the line of intersection. | |||
The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2. | |||
It is obvious that the product of two reflections is a rotation. Indeed, a reflection is an [[isometry]] and has [[determinant]] −1. The product of two isometric operators is again an isometry and the rule for determinants is det(''AB'') = det(''A'')det(''B''), so that the product of two reflections is an isometry with unit determinant, i.e., a rotation. | |||
Let the normal of the first plane be <math>\vec{\mathbf{s}}</math> and of the second <math>\vec{\mathbf{t}}</math>, then the rotation is represented by the matrix | |||
:<math> | |||
\left[ \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} \right]\, \left[ \mathbf{E} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} \right] | |||
= \mathbf{E} - \frac{2}{t^2} \vec{\mathbf{t}} \otimes\vec{\mathbf{t}} - \frac{2}{s^2} \vec{\mathbf{s}} \otimes\vec{\mathbf{s}} + \frac{4}{t^2 s^2} (\vec{\mathbf{t}}\cdot\vec{\mathbf{s}})\; | |||
\big(\vec{\mathbf{t}} \otimes\vec{\mathbf{s}}\big) | |||
</math> | |||
The ''(i,j)'' element if this matrix is equal to | |||
:<math> | |||
\delta_{ij} - \frac{2 t_i t_j }{t^2} - \frac{2 s_i s_j }{s^2} + \frac{4 t_i s_j (\sum_k t_k s_k)}{t^2 s^2} . | |||
</math> | |||
This formula is used in [[vector rotation]].[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:00, 10 October 2024
In Euclidean geometry, a reflection is a linear operation σ on with σ2 = E, the identity map. This property of σ is called involution. An involutory operator is non-singular and σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :
The operation σ is an isometry of onto itself, which means that it preserves inner products and that its inverse is equal to its adjoint,
Hence reflection is also symmetric: σT = σ. From (det(σ))2 = det(E) = 1 follows that isometries have determinant ±1. Those with positive determinant are rotations, while reflections have determinant −1. Because σ is symmetric it has real eigenvalues; since the extension of an isometry to a complex space is unitary, its (complex) eigenvalues have modulus 1. It follows that the eigenvalues of σ are ±1. The product of the eigenvalues being its determinant, −1, the sets of eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to −E, minus the identity operator. This operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article. Sometimes one finds the concept of "reflections in a line", these are rotations over 180°, see rotation matrix.
Reflection in a plane
If is a unit vector normal (perpendicular) to a plane—the mirror plane—then is the projection of on this unit vector. From the figure it is evident that
If a non-unit normal is used then substitution of
gives the mirror image,
Sometimes it is convenient to write this as a matrix equation. Introducing the dyadic product, we obtain
where E is the 3×3 identity matrix.
Dyadic products satisfy the matrix multiplication rule
By the use of this rule it is easily shown that
which confirms that reflection is involutory.
Reflection in a plane not through the origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector . The length of this vector is the distance from O to the plane. From Figure 2, we find
Use of the equation derived earlier gives
And hence the equation for the reflected pair of vectors is,
where is a unit vector normal to the plane. Obviously and are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of ,
Two consecutive reflections
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 3, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
It is obvious that the product of two reflections is a rotation. Indeed, a reflection is an isometry and has determinant −1. The product of two isometric operators is again an isometry and the rule for determinants is det(AB) = det(A)det(B), so that the product of two reflections is an isometry with unit determinant, i.e., a rotation.
Let the normal of the first plane be and of the second , then the rotation is represented by the matrix
The (i,j) element if this matrix is equal to
This formula is used in vector rotation.













![{\displaystyle {\vec {\mathbf {r} }}\,'=\left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]\;{\vec {\mathbf {r} }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb112d732fbaf7c81a05f819922f6b4d713dc646)
![{\displaystyle [{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {b} }}]\,[{\vec {\mathbf {c} }}\otimes {\vec {\mathbf {d} }}]=({\vec {\mathbf {b} }}\cdot {\vec {\mathbf {c} }}){\big (}{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {d} }}{\big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037a6b38897a0d8a8d7787a0ea60a4e18d091281)
![{\displaystyle \left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]^{2}=\mathbf {E} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd65ff7a8f5970ebba0e77e1a5680c6192a28266)







![{\displaystyle \left[\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}\right]\,\left[\mathbf {E} -{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}\right]=\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}-{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}+{\frac {4}{t^{2}s^{2}}}({\vec {\mathbf {t} }}\cdot {\vec {\mathbf {s} }})\;{\big (}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {s} }}{\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/454d07547f582382357684b9dc6463f3ff0ecbbc)
