Molecular dipole: Difference between revisions
imported>Paul Wormer |
mNo edit summary |
||
| (24 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
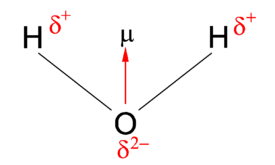
{{Image|Water dipole.png|right|275px|Fig. 1. The dipole '''μ''' of the water molecule. The molecule is electrically neutral: <math>2\delta^+ + \delta^{2-}=0.</math> Because of symmetry the vector has one non-vanishing component; it points from the negative to the positive region of the molecule.}} | |||
Molecular dipole moments may be obtained experimentally; the main techniques are [[microwave spectroscopy]] and measurements of [[dielectric constant]]s. Dipole moments can be computed reliably for smaller molecules (say up to 10 second-period atoms) by means of quantum chemical methods. | Being a charge distribution, a [[molecule]] may possess a permanent [[electric dipole]], a [[vector]] known as the '''molecular dipole'''. The size of this dipole, referred to as the ''molecular dipole moment'', gives an indication of the ''polarity'' of the molecule, that is, the dipole moment is a measure for the amount of charge separation in a molecule. | ||
In chemistry, polarity is usually explained by the presence of [[electronegativity|electronegative]] and/or [[electropositivity|electropositive]] atoms in the molecule. An electronegative atom attracts electrons (becomes negative) and an electropositive atom donates electrons (becomes positive). These concepts are semi-quantitative and different scales for electronegativity and electropositivity of the [[chemical element]]s are in use, leading to differing values of molecular dipole moments. However, all scales predict the same direction of the dipole. For physicists the direction of the dipole vector is from negative to positive charge and for many chemists it is the opposite, namely from positive to negative charge. The figure shows the dipole moment of water in the physics convention. | |||
Molecular dipole moments may be obtained experimentally; the main techniques are [[microwave spectroscopy]] and measurements of [[dielectric constant]]s as function of temperature. Dipole moments can be computed reliably for smaller molecules (say up to 10 second-period atoms) by means of quantum chemical methods. | |||
==Selection rule== | ==Selection rule== | ||
Whether a molecule has one or more non-zero permanent dipole components depends on the [[molecular symmetry|symmetry]] of the molecule and on the symmetry species of the molecular state under consideration. Symmetry arguments can | Whether a molecule has one or more non-zero permanent dipole components depends on the [[molecular symmetry|symmetry]] of the molecule and on the symmetry species of the molecular state under consideration. Symmetry arguments can explain the vanishing of components of a molecular dipole (symmetry gives a "[[selection rule]]"), but symmetry arguments cannot directly predict the magnitudes of the non-vanishing components. Conversely, if measurements show that a molecular dipole is zero, it gives an indication of the symmetry of the molecule. For instance, if the gas phase molecule CO<sub>2</sub> were bent, like H<sub>2</sub>O, it would have an observable dipole. Since it has not, its structure is in all likelihood linear. Spectroscopic measurements and quantum chemical calculations have confirmed the linearity of CO<sub>2</sub>. | ||
Usually one considers molecules in their ground | Usually one considers molecules in their ground (lowest energy) electronic state and this state is almost always totally symmetric, i.e., invariant under ''all'' symmetry operations. Provided a molecule is in a totally symmetric state, it can be shown that a dipole component vanishes when it is not totally symmetric (not invariant under all symmetry operations). As an example, the rule explains why the molecular dipole moments in figure 1 (water) and in figure 2 (orthodichlorobenzene) are in the vertical and horizontal mirror plane of their molecule; reflection in a plane that contains a dipole leaves the dipole invariant. For the same reason the dipoles in the examples lie along the (twofold) rotation axis of their molecule. | ||
This rule can be proved formally, but can also be understood intuitively. By definition a symmetry operation changes a molecule to a conformation that is indistinguishable from the original conformation. If a dipole component would change under a symmetry operation, it would give a | This rule can be proved formally, but can also be understood intuitively. By definition a symmetry operation changes a molecule to a conformation that is indistinguishable from the original conformation. If a dipole component would change under a symmetry operation, it would give a means to distinguish the old from the new conformation, so that the two conformations would be distinguishable. This is a contradiction and, hence, either a dipole component is zero or it is invariant, i.e., does not change under any of the symmetry operations. | ||
More technically: the symmetry operations of a molecule that is rigid—i.e., the nuclei are clamped in space, but the electrons "move" in the quantum mechanical sense of the word—form a [[group]], the ''[[point group]]'' of the molecule. This point group has [[irreducible representations]] among which is the totally symmetric one, commonly denoted by ''A''<sub>1</sub>. Most molecular ground states transform as ''A''<sub>1</sub> (alternatively expressed as: "the symmetry species of the ground state is ''A''<sub>1</sub>"). Only the components of the dipole that transform according to ''A''<sub>1</sub> are non-vanishing. This is true not only for molecules in an ''A''<sub>1</sub> state, but holds for molecules in any non-degenerate state (a state that transforms according to a one-dimensional irreducible representation of the point group). | More technically: the symmetry operations of a molecule that is rigid—i.e., the nuclei are clamped in space, but the electrons "move" in the quantum mechanical sense of the word—form a [[group]], the ''[[point group]]'' of the molecule. This point group has [[irreducible representations]] among which is the totally symmetric one, commonly denoted by ''A''<sub>1</sub>. Most molecular ground states transform as ''A''<sub>1</sub> (alternatively expressed as: "the symmetry species of the ground state is ''A''<sub>1</sub>"). Only the components of the dipole that transform according to ''A''<sub>1</sub> are non-vanishing. This is true not only for molecules in an ''A''<sub>1</sub> state, but holds for molecules in any non-degenerate state (a state that transforms according to a one-dimensional irreducible representation of the point group). | ||
| Line 17: | Line 20: | ||
Molecules with an inversion center, such as [[ethene]] (C<sub>2</sub>H<sub>4</sub>) and [[sulfur hexafluoride]] (SF<sub>6</sub>), do not have a permanent dipole moment because all three components of the dipole change sign under inversion (are non-invariant). | Molecules with an inversion center, such as [[ethene]] (C<sub>2</sub>H<sub>4</sub>) and [[sulfur hexafluoride]] (SF<sub>6</sub>), do not have a permanent dipole moment because all three components of the dipole change sign under inversion (are non-invariant). | ||
Note that the presence of an inversion center is not | Note that the presence of an inversion center is not necessary for the vanishing of permanent dipoles, for instance, [[methane]] (CH<sub>4</sub>) is a tetrahedrally shaped molecule without an inversion center and yet has no permanent dipole. The point group of methane is the tetrahedral group T<sub>d</sub>. The components of the dipole span a 3-dimensional irreducible representation of this group, so that none of the three components is invariant under the operations of T<sub>d</sub>; all three components vanish when methane is in a non-degenerate electronic state. | ||
==Bond dipoles== | |||
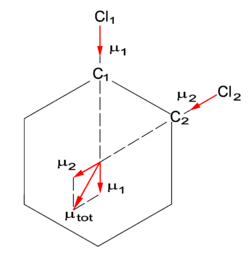
{{Image|Orthodichlorobenzene.png|right|250px|Fif. 2. Addition of two bond dipoles in orthodichlorobenzene. The atoms Cl<sub>1</sub> and Cl<sub>2</sub> are more electronegative than the carbon atoms to which they are bound, hence the directions of the bond dipoles '''μ'''<sub>1</sub> and '''μ'''<sub>2</sub>. The vector '''μ'''<sub>tot</sub> is the total molecular dipole.}} | |||
There is an approximate way of predicting the size of the molecular dipole moments. To each bonded pair of atoms a ''bond dipole'' is assigned and the bond dipoles are added vectorially to a total dipole moment of the molecule. Equal bonds have equal dipoles. The method is illustrated in figure 2 for the molecule orthodichlorobenzene that has two large bond dipoles '''μ'''<sub>1</sub> and '''μ'''<sub>2</sub> along the C–Cl bonds. The four C–H bond dipoles in the molecule are much smaller and are neglected. (The two C–H bond dipoles in ''meta'' position cancel mutually and the other two give a small modification of '''μ'''<sub>1</sub> and '''μ'''<sub>2</sub>, respectively.) | |||
In this way one can predict without knowledge of symmetry or group theory that certain dipoles vanish. For instance, the linear molecule O–C–O has no dipole because the two C–O bond dipoles are antiparallel and cancel each other. (By the symmetry argument it follows from the presence of an inversion center that that O–C–O has no dipole.) As another example we mention that in the case of [[methane]] (CH<sub>4</sub>), a tetrahedrally shaped molecule, the four C–H bond dipoles add up to zero. It is apparent that in the addition of the four bond dipoles it must be used that these vectors point from the center of the regular tetrahedral molecule to its vertices. Hence the symmetry of methane is used implicitly in this argument. | |||
A clear advantage of the bond dipole method is that, given a table of bond dipoles (and the assumption that these are transferable between different molecules) a fair estimate of the total molecular dipole is obtained by the vector addition of the bond dipoles. | |||
==Units and order of magnitude== | ==Units and order of magnitude== | ||
An electric dipole moment has the dimension charge times length. The [[SI]] unit of dipole is accordingly [[coulomb]] times [[meter]]. However, this unit is unwieldly large and therefore hardly used in chemistry and molecular physics. The [[Gaussian unit]] of [[debye]] (D) is most widely applied | An electric dipole moment has the dimension charge times length. The [[SI]] unit of dipole is accordingly [[coulomb]] times [[meter]]. However, this unit is unwieldly large and therefore hardly used in chemistry and molecular physics. The [[Gaussian unit]]s-based unit of [[debye]] (D) is most widely applied: | ||
: 1 D = 10<sup>−10</sup> esu • [[ångstrom]]. | |||
An ångstrom is 10<sup>−8</sup> cm = 10<sup>−10</sup> m. An esu (electrostatic unit of charge, modern name [[statcoulomb]]) is C/(10⋅''c'') ≈ 3.335 640 95⋅10<sup>−10</sup> C, where C is coulomb and ''c'' is [[speed of light]] (≈ 3⋅10<sup>8</sup> m/s). Hence, | |||
:<math> | :<math> | ||
1\; \mathrm{D} = | 1\; \mathrm{D} = \frac{10^{-20}}{10 c}\; \mathrm{C\,m} \approx 3.335\,640\,95\cdot 10^{-30}\;\; \mathrm{C\,m} . | ||
</math> | </math> | ||
The unit is named after the Dutch/American chemical physicist [[Peter Debye]]. | |||
In quantum chemistry and molecular physics a common unit of dipole moment is the [[atomic unit]]: | In quantum chemistry and molecular physics, a common unit of dipole moment is the [[atomic unit]]: | ||
the charge ''e'' of an electron times the [[bohr radius]] ''a''<sub>0</sub>. | the charge ''e'' of an electron times the [[bohr radius]] ''a''<sub>0</sub>. | ||
Since 1 ''e'' = 1.602 176 487 ⋅ 10<sup>−19</sup> C and ''a''<sub>0</sub> = 0.529 177 208 59 ⋅ 10<sup>−10</sup> m, it follows that | Since 1 ''e'' = 1.602 176 487 ⋅ 10<sup>−19</sup> C and ''a''<sub>0</sub> = 0.529 177 208 59 ⋅ 10<sup>−10</sup> m, it follows that | ||
| Line 35: | Line 46: | ||
</math> | </math> | ||
The debye is of such magnitude that most molecules have dipole moments on the order of 1 to 10 D. For instance, water has an electric dipole moment of 1.85 D and HCl has 1.09 D. In both cases the direction of the dipole is determined by the fact that the hydrogen atom(s) is(are) slightly positive. | The debye is of such magnitude that most molecules have dipole moments on the order of 1 to 10 D. For instance, the water molecule, shown in figure 1, has an electric dipole moment of 1.85 D and HCl has 1.09 D. In both cases the direction of the dipole is determined by the fact that the hydrogen atom(s) is(are) slightly positive. Hence, in HCl the dipole points from Cl to H (in the physics convention). | ||
==Quantum mechanical theory== | ==Quantum mechanical theory== | ||
<font style = "font-size: 80%; font-style: oblique; font-weight: bolder" > | |||
As an observable a dipole is represented by a [[Hermitian operator]] on the state space of | :A few remarks are made about the quantum mechanical background of the molecular dipole. Readers without knowledge of quantum mechanics are advised to skip this section.</font> | ||
===Dipole operator=== | |||
As an observable property, a dipole is represented by a [[Hermitian operator]] on the state space of | |||
the molecule. This operator is obtained from the corresponding classical expression by | the molecule. This operator is obtained from the corresponding classical expression by | ||
reinterpreting the spatial coordinates as multiplicative operators. Classically a molecule | reinterpreting the spatial coordinates as multiplicative operators. Classically a molecule | ||
| Line 47: | Line 61: | ||
</math> | </math> | ||
where δ is the [[Dirac delta function]]. | where δ is the [[Dirac delta function]]. | ||
Classically, the dipole is the first moment of this charge distribution, | |||
:<math> | :<math> | ||
\boldsymbol{\mu} \equiv \int \mathbf{r}\,\rho(\mathbf{r}) \; \mathrm{d}\mathbf{r} = | \boldsymbol{\mu} \equiv \int \mathbf{r}\,\rho(\mathbf{r}) \; \mathrm{d}\mathbf{r} = | ||
\sum_{k=1}^N q_k\, \mathbf{r}_k | \sum_{k=1}^N q_k\, \mathbf{r}_k . | ||
</math> | </math> | ||
The rightmost expression is the quantum mechanical dipole operator, where the sum is over | The rightmost expression is the quantum mechanical dipole operator, where the sum is over | ||
electrons ''and'' nuclei. | electrons ''and'' nuclei. | ||
===Interaction with electric field=== | |||
When the molecule is brought into an [[electric field]] '''F''' it obtains an energy with | When the molecule is brought into an [[electric field]] '''F''' it obtains an energy with | ||
operator | operator | ||
:<math> | :<math> | ||
V = \boldsymbol{\mu}\cdot \mathbf{ | V = -\mathbf{F} \cdot\boldsymbol{\mu} = -\mathbf{F}\cdot \left(\sum_{k=1}^N \, q_k \; \mathbf{r}_k\right), | ||
</math> | </math> | ||
which is added to the usual field-free [[Hamiltonian]] ''H''<sub>0</sub> of the molecule. If one | which is added to the usual field-free [[Hamiltonian]] ''H''<sub>0</sub> of the molecule. | ||
solves the Schrödinger equation with total Hamiltonian ''H'' = ''H''<sub>0</sub> + ''V'' one obtains | ===Definition observed dipole=== | ||
energy ''E'' and a corresponding wave function Ψ | If one solves the Schrödinger equation with total Hamiltonian ''H'' = ''H''<sub>0</sub> + ''V'' one obtains a total energy ''E''('''F''') and a corresponding wave function Ψ('''F'''), both depending on '''F'''. We assume that the state Ψ is non-degenerate. The observed dipole is given by the first derivative (it is a so-called first-order response property, a second-order response property is a second derivative, third derivative gives a third-order response property, and so on), | ||
:<math> | :<math> | ||
\boldsymbol{\mu}_\mathrm{obs} | \boldsymbol{\mu}_\mathrm{obs} \; \stackrel{\mathrm{def}}{=}\;- \left( \frac{\partial E(\mathbf{F})}{\partial | ||
\mathbf{F}}\right)_{\mathbf{F} = \mathbf{0}} | \mathbf{F}}\right)_{\mathbf{F} = \mathbf{0}}. | ||
</math> | </math> | ||
===Hellmann-Feynman theorem=== | |||
When the [[Hellmann-Feynman theorem|Hellmann-Feynman]] (H-F) theorem holds, a much simplified expression for the observed dipole may be derived. Use that | |||
:<math> | :<math> | ||
E = \langle \Psi(\mathbf{F})\; |\;H_0 + V\; |\; \Psi(\mathbf{F})\rangle | E(\mathbf{F}) = \langle \Psi(\mathbf{F})\; |\;H_0 + V\; |\; \Psi(\mathbf{F})\rangle | ||
\equiv \langle \Psi(\mathbf{F})\; |\;H\; |\; \Psi(\mathbf{F})\rangle | |||
\quad\hbox{with}\quad \langle \Psi(\mathbf{F})\; |\;\Psi(\mathbf{F})\rangle = 1, | |||
</math> | </math> | ||
we get | and we get | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
\boldsymbol{\mu}_\mathrm{obs} & = | \boldsymbol{\mu}_\mathrm{obs} & = - | ||
\left(\frac{\partial \langle \Psi(\mathbf{F})\; |\;H \;|\; | \left(\frac{\partial \langle \Psi(\mathbf{F})\; |\;H \;|\; | ||
\Psi(\mathbf{F})\rangle }{\partial \mathbf{F}}\right)_{\mathbf{F} = \mathbf{0}} \\ | \Psi(\mathbf{F})\rangle }{\partial \mathbf{F}}\right)_{\mathbf{F} = \mathbf{0}} \\ | ||
&=\Big \langle \frac{\partial\Psi(\mathbf{F})}{\partial \mathbf{F}}\;|\; H \;|\;\Psi(\mathbf{F}) \Big\rangle_{\mathbf{F} = \mathbf{0}} | &=-\Big \langle \frac{\partial\Psi(\mathbf{F})}{\partial \mathbf{F}}\;|\; H \;|\;\Psi(\mathbf{F}) \Big\rangle_{\mathbf{F} = \mathbf{0}} - | ||
\Big\langle \Psi(\mathbf{F}) \;|\; H \;|\; \frac{\partial \Psi(\mathbf{F})}{\partial \mathbf{F}} | \Big\langle \Psi(\mathbf{F}) \;|\; H \;|\; \frac{\partial \Psi(\mathbf{F})}{\partial \mathbf{F}} | ||
\Big\rangle_{\mathbf{F} | \Big\rangle_{\mathbf{F} = \mathbf{0}} + \langle \Psi(\mathbf{0}) \;|\; \boldsymbol{\mu}\;|\;\Psi(\mathbf{0}) \rangle, | ||
= \mathbf{0}} + | |||
\langle \Psi(\mathbf{0}) \;|\; \boldsymbol{\mu}\;|\;\Psi(\mathbf{0}) \rangle | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
where we used that | |||
:<math> | |||
\frac{\partial H} {\partial \mathbf{F}} = \frac{\partial V} {\partial \mathbf{F}} =- \boldsymbol{\mu}. | |||
</math> | |||
The Hellmann-Feynman theorem (that holds if Ψ is an exact eigenfunction of ''H'') states, | |||
is an exact eigenfunction of ''H'') | |||
:<math> | :<math> | ||
\Big \langle \frac{\partial\Psi(\mathbf{F})}{\partial \mathbf{F}}\;|\; H \;|\;\Psi(\mathbf{F}) \Big\rangle + | \Big \langle \frac{\partial\Psi(\mathbf{F})}{\partial \mathbf{F}}\;|\; H \;|\;\Psi(\mathbf{F}) \Big\rangle + | ||
\Big\langle \Psi(\mathbf{F}) \;|\; H \;|\; \frac{\partial \Psi(\mathbf{F})}{\partial \mathbf{F}} \Big\rangle | \Big\langle \Psi(\mathbf{F}) \;|\; H \;|\; \frac{\partial \Psi(\mathbf{F})}{\partial \mathbf{F}} \Big\rangle | ||
= 0 | = 0 . | ||
</math> | </math> | ||
When the theorem holds the observed dipole is given as an expectation value | When the H-F theorem holds the observed dipole is given as an ''expectation (average) value'' | ||
:<math> | :<math> | ||
\boldsymbol{\mu}_\mathrm{obs} = \langle\; \Psi(\mathbf{0})\; |\; | \boldsymbol{\mu}_\mathrm{obs} = \langle\; \Psi(\mathbf{0})\; |\; | ||
\boldsymbol{\mu}\;|\;\Psi(\mathbf{0}) \;\rangle. | \boldsymbol{\mu}\;|\;\Psi(\mathbf{0}) \;\rangle. | ||
</math> | </math> | ||
The wave function Ψ('''0''') does not depend on '''F'''. It is | The wave function Ψ('''0''') does not depend on '''F'''. It is an eigenfunction of the field-free molecular Hamiltonian ''H''<sub>0</sub>. This function is not perturbed by ''V'', and is referred to as zeroth-order in V, so that the observed dipole is the first derivative of the first-order [[perturbation theory|perturbation energy]], | ||
an eigenfunction of the field-free molecular Hamiltonian ''H''<sub>0</sub>. | :<math> | ||
This function is not perturbed by ''V'', and is referred to as zeroth-order in V, | E^{(1)} \equiv \langle\, \Psi^{(0)}\, |\, V \,|\, \Psi^{(0)}\,\rangle | ||
so that the observed dipole is the first derivative of the first-order energy, | \quad\hbox{with}\quad \langle\, \Psi^{(0)}\, |\,\Psi^{(0)}\,\rangle = 1, | ||
</math> | |||
whenever the H-F theorem holds, | |||
:<math> | :<math> | ||
\boldsymbol{\mu}_\mathrm{obs} | \boldsymbol{\mu}_\mathrm{obs} =- \frac{\partial E^{(1)}}{\partial \mathbf{F}} = - | ||
\frac{\partial \langle \Psi^{(0)} | V | \Psi^{(0)}\rangle }{\partial \mathbf{F}} | \frac{\partial \langle \Psi^{(0)} | V | \Psi^{(0)}\rangle }{\partial \mathbf{F}} | ||
= \langle \Psi^{(0)} | \boldsymbol{\mu} | \Psi^{(0)}\rangle | = \langle\, \Psi^{(0)}\, |\, \boldsymbol{\mu} \,|\, \Psi^{(0)}\,\rangle | ||
\quad\hbox{with}\quad \Psi^{(0)} \equiv \Psi(\mathbf{0}). | \quad\hbox{with}\quad \Psi^{(0)} \equiv \Psi(\mathbf{0}). | ||
</math> | </math> | ||
There are computational methods yielding | There are computational methods yielding results that do ''not'' obey the | ||
Hellmann-Feynman theorem | Hellmann-Feynman theorem, or, in other words, the first derivative of the total energy does not give the same result as the first derivative of the first-order energy. It is generally found that the derivative of the total energy (computed in the presence of a field) is the more reliable route to '''μ'''. It is also the more expensive route because the computation of '''μ''' is usually done by numerical differentiation. This requires the computation of the total energy for several different values of '''F''', while the route via the first-order energy only requires the computation of the expectation value of '''μ'''. Some quantum chemical methods only give energies, not wave functions; for those methods the derivative with respect to the field is the only computational access to the dipole moment. | ||
derivative of the total energy does not give the same result as the first derivative of | |||
the first-order energy. It is generally found that the derivative of the total energy | |||
(computed in the presence of a field) is the more reliable route to '''μ'''. It is also | |||
numerical differentiation. | |||
This requires the computation of the total energy for several different values of '''F''', | |||
while the route via the first-order energy only requires the computation of the | |||
expectation value of '''μ'''. | |||
To avoid misunderstanding we reiterate that the Hellman-Feynman theorem holds for exact eigenfunctions, so that the expression for '''μ'''<sub>obs</sub> as an expectation value over unperturbed eigenfunctions is true for exact wave functions. | |||
===Symmetry=== | |||
In order to indicate how symmetry can predict the vanishing of a molecular dipole, we | In order to indicate how symmetry can predict the vanishing of a molecular dipole, we | ||
consider the first-order formula and space inversion (parity) Π. Parity is a | consider the first-order formula and space inversion (parity) Π. Parity is a | ||
[[unitary operator]]. Assume | [[unitary operator]]. Assume that the non-degenerate zeroth-order wave function has definite (odd or even) parity, | ||
:<math> | :<math> | ||
\Pi \Psi^{(0)} = \pm \Psi^{(0)} | \Pi \Psi^{(0)} = \pm \Psi^{(0)}. | ||
</math> | </math> | ||
We know, because position vectors change sign, that | |||
:<math> | :<math> | ||
\Pi \, \boldsymbol{\mu} \Pi^\dagger = -\boldsymbol{\mu}\quad\hbox{ | \Pi \, \boldsymbol{\mu} \Pi^\dagger = -\boldsymbol{\mu}\quad\hbox{with}\quad | ||
\Pi^\dagger\Pi = 1. | \Pi^\dagger\,\Pi = 1. | ||
</math> | </math> | ||
Now | Now | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
\boldsymbol{\mu}_\mathrm{obs} &= \langle \Psi( | \boldsymbol{\mu}_\mathrm{obs} &= \langle \Psi^{(0)} \;|\; \Pi^\dagger \, \Pi | ||
\,\boldsymbol{\mu}\,\Pi^\dagger\, \Pi\;|\;\Psi( | \,\boldsymbol{\mu}\,\Pi^\dagger\, \Pi\;|\;\Psi^{(0)} \rangle \\ | ||
& = | & = | ||
\langle \Pi\, \Psi( | \langle \Pi\, \Psi^{(0)} \;|\; -\boldsymbol{\mu}\;|\; \Pi\,\Psi^{(0)} \rangle \\ | ||
&= - (\pm)^2\langle | &= - (\pm)^2\langle \Psi^{(0)} |\boldsymbol{\mu}| \Psi^{(0)}\rangle | ||
= - \boldsymbol{\mu}_\mathrm{obs}, | = - \boldsymbol{\mu}_\mathrm{obs}, | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
where we used that the adjoint of Π, moved to the bra, becomes Π. And finally | where we used that the adjoint Π<sup>†</sup> of Π, moved to the bra, becomes Π. And finally | ||
:<math> | :<math> | ||
\boldsymbol{\mu}_\mathrm{obs} = - \boldsymbol{\mu}_\mathrm{obs} | \boldsymbol{\mu}_\mathrm{obs} = - \boldsymbol{\mu}_\mathrm{obs} | ||
\;\Longrightarrow\; \boldsymbol{\mu}_\mathrm{obs}= 0 | \;\Longrightarrow\; \boldsymbol{\mu}_\mathrm{obs}= 0 . | ||
</math> | </math> | ||
This argument can generalized to arbitrary point groups and leads to the rule: | This argument can be generalized to arbitrary point groups and leads to the rule: | ||
the product of the symmetry species (irreducible representations) of bra, ket, and | the product of the symmetry species (irreducible representations) of bra, ket, and | ||
operator (component of dipole) must contain the totally symmetric representation in | operator (component of dipole) must contain the totally symmetric representation in | ||
order that the expectation value of the operator does not vanish. | order that the expectation value of the operator does not vanish. | ||
Since an atom has inversion symmetry, this reasoning shows that no atom in a non-degenerate state (an ''S''-state, a spherically symmetric state) can have a permanent dipole. In the case of open-shell atoms with degenerate energy levels, one could define a dipole moment by the aid of the first-order [[Stark effect]]. This only gives a non-vanishing dipole (by definition proportional to a non-vanishing first-order Stark shift) if some of the wave functions belonging to the degenerate energies have opposite parity; i.e., have different behavior under inversion. This is a rare occurrence, but happens for the first-excited H-atom, where 2s and 2p states are "accidentally" degenerate and have opposite parity (2s is even and 2p is odd).[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:00, 20 September 2024
Being a charge distribution, a molecule may possess a permanent electric dipole, a vector known as the molecular dipole. The size of this dipole, referred to as the molecular dipole moment, gives an indication of the polarity of the molecule, that is, the dipole moment is a measure for the amount of charge separation in a molecule.
In chemistry, polarity is usually explained by the presence of electronegative and/or electropositive atoms in the molecule. An electronegative atom attracts electrons (becomes negative) and an electropositive atom donates electrons (becomes positive). These concepts are semi-quantitative and different scales for electronegativity and electropositivity of the chemical elements are in use, leading to differing values of molecular dipole moments. However, all scales predict the same direction of the dipole. For physicists the direction of the dipole vector is from negative to positive charge and for many chemists it is the opposite, namely from positive to negative charge. The figure shows the dipole moment of water in the physics convention.
Molecular dipole moments may be obtained experimentally; the main techniques are microwave spectroscopy and measurements of dielectric constants as function of temperature. Dipole moments can be computed reliably for smaller molecules (say up to 10 second-period atoms) by means of quantum chemical methods.
Selection rule
Whether a molecule has one or more non-zero permanent dipole components depends on the symmetry of the molecule and on the symmetry species of the molecular state under consideration. Symmetry arguments can explain the vanishing of components of a molecular dipole (symmetry gives a "selection rule"), but symmetry arguments cannot directly predict the magnitudes of the non-vanishing components. Conversely, if measurements show that a molecular dipole is zero, it gives an indication of the symmetry of the molecule. For instance, if the gas phase molecule CO2 were bent, like H2O, it would have an observable dipole. Since it has not, its structure is in all likelihood linear. Spectroscopic measurements and quantum chemical calculations have confirmed the linearity of CO2.
Usually one considers molecules in their ground (lowest energy) electronic state and this state is almost always totally symmetric, i.e., invariant under all symmetry operations. Provided a molecule is in a totally symmetric state, it can be shown that a dipole component vanishes when it is not totally symmetric (not invariant under all symmetry operations). As an example, the rule explains why the molecular dipole moments in figure 1 (water) and in figure 2 (orthodichlorobenzene) are in the vertical and horizontal mirror plane of their molecule; reflection in a plane that contains a dipole leaves the dipole invariant. For the same reason the dipoles in the examples lie along the (twofold) rotation axis of their molecule.
This rule can be proved formally, but can also be understood intuitively. By definition a symmetry operation changes a molecule to a conformation that is indistinguishable from the original conformation. If a dipole component would change under a symmetry operation, it would give a means to distinguish the old from the new conformation, so that the two conformations would be distinguishable. This is a contradiction and, hence, either a dipole component is zero or it is invariant, i.e., does not change under any of the symmetry operations.
More technically: the symmetry operations of a molecule that is rigid—i.e., the nuclei are clamped in space, but the electrons "move" in the quantum mechanical sense of the word—form a group, the point group of the molecule. This point group has irreducible representations among which is the totally symmetric one, commonly denoted by A1. Most molecular ground states transform as A1 (alternatively expressed as: "the symmetry species of the ground state is A1"). Only the components of the dipole that transform according to A1 are non-vanishing. This is true not only for molecules in an A1 state, but holds for molecules in any non-degenerate state (a state that transforms according to a one-dimensional irreducible representation of the point group).
Molecules with an inversion center, such as ethene (C2H4) and sulfur hexafluoride (SF6), do not have a permanent dipole moment because all three components of the dipole change sign under inversion (are non-invariant).
Note that the presence of an inversion center is not necessary for the vanishing of permanent dipoles, for instance, methane (CH4) is a tetrahedrally shaped molecule without an inversion center and yet has no permanent dipole. The point group of methane is the tetrahedral group Td. The components of the dipole span a 3-dimensional irreducible representation of this group, so that none of the three components is invariant under the operations of Td; all three components vanish when methane is in a non-degenerate electronic state.
Bond dipoles
There is an approximate way of predicting the size of the molecular dipole moments. To each bonded pair of atoms a bond dipole is assigned and the bond dipoles are added vectorially to a total dipole moment of the molecule. Equal bonds have equal dipoles. The method is illustrated in figure 2 for the molecule orthodichlorobenzene that has two large bond dipoles μ1 and μ2 along the C–Cl bonds. The four C–H bond dipoles in the molecule are much smaller and are neglected. (The two C–H bond dipoles in meta position cancel mutually and the other two give a small modification of μ1 and μ2, respectively.)
In this way one can predict without knowledge of symmetry or group theory that certain dipoles vanish. For instance, the linear molecule O–C–O has no dipole because the two C–O bond dipoles are antiparallel and cancel each other. (By the symmetry argument it follows from the presence of an inversion center that that O–C–O has no dipole.) As another example we mention that in the case of methane (CH4), a tetrahedrally shaped molecule, the four C–H bond dipoles add up to zero. It is apparent that in the addition of the four bond dipoles it must be used that these vectors point from the center of the regular tetrahedral molecule to its vertices. Hence the symmetry of methane is used implicitly in this argument.
A clear advantage of the bond dipole method is that, given a table of bond dipoles (and the assumption that these are transferable between different molecules) a fair estimate of the total molecular dipole is obtained by the vector addition of the bond dipoles.
Units and order of magnitude
An electric dipole moment has the dimension charge times length. The SI unit of dipole is accordingly coulomb times meter. However, this unit is unwieldly large and therefore hardly used in chemistry and molecular physics. The Gaussian units-based unit of debye (D) is most widely applied:
- 1 D = 10−10 esu • ångstrom.
An ångstrom is 10−8 cm = 10−10 m. An esu (electrostatic unit of charge, modern name statcoulomb) is C/(10⋅c) ≈ 3.335 640 95⋅10−10 C, where C is coulomb and c is speed of light (≈ 3⋅108 m/s). Hence,
The unit is named after the Dutch/American chemical physicist Peter Debye.
In quantum chemistry and molecular physics, a common unit of dipole moment is the atomic unit: the charge e of an electron times the bohr radius a0. Since 1 e = 1.602 176 487 ⋅ 10−19 C and a0 = 0.529 177 208 59 ⋅ 10−10 m, it follows that
The debye is of such magnitude that most molecules have dipole moments on the order of 1 to 10 D. For instance, the water molecule, shown in figure 1, has an electric dipole moment of 1.85 D and HCl has 1.09 D. In both cases the direction of the dipole is determined by the fact that the hydrogen atom(s) is(are) slightly positive. Hence, in HCl the dipole points from Cl to H (in the physics convention).
Quantum mechanical theory
- A few remarks are made about the quantum mechanical background of the molecular dipole. Readers without knowledge of quantum mechanics are advised to skip this section.
Dipole operator
As an observable property, a dipole is represented by a Hermitian operator on the state space of the molecule. This operator is obtained from the corresponding classical expression by reinterpreting the spatial coordinates as multiplicative operators. Classically a molecule is a charge distribution consisting of N point charges qk at positions rk (electrons and nuclei),
where δ is the Dirac delta function. Classically, the dipole is the first moment of this charge distribution,
The rightmost expression is the quantum mechanical dipole operator, where the sum is over electrons and nuclei.
Interaction with electric field
When the molecule is brought into an electric field F it obtains an energy with operator
which is added to the usual field-free Hamiltonian H0 of the molecule.
Definition observed dipole
If one solves the Schrödinger equation with total Hamiltonian H = H0 + V one obtains a total energy E(F) and a corresponding wave function Ψ(F), both depending on F. We assume that the state Ψ is non-degenerate. The observed dipole is given by the first derivative (it is a so-called first-order response property, a second-order response property is a second derivative, third derivative gives a third-order response property, and so on),
Hellmann-Feynman theorem
When the Hellmann-Feynman (H-F) theorem holds, a much simplified expression for the observed dipole may be derived. Use that
and we get
where we used that
The Hellmann-Feynman theorem (that holds if Ψ is an exact eigenfunction of H) states,
When the H-F theorem holds the observed dipole is given as an expectation (average) value
The wave function Ψ(0) does not depend on F. It is an eigenfunction of the field-free molecular Hamiltonian H0. This function is not perturbed by V, and is referred to as zeroth-order in V, so that the observed dipole is the first derivative of the first-order perturbation energy,
whenever the H-F theorem holds,
There are computational methods yielding results that do not obey the Hellmann-Feynman theorem, or, in other words, the first derivative of the total energy does not give the same result as the first derivative of the first-order energy. It is generally found that the derivative of the total energy (computed in the presence of a field) is the more reliable route to μ. It is also the more expensive route because the computation of μ is usually done by numerical differentiation. This requires the computation of the total energy for several different values of F, while the route via the first-order energy only requires the computation of the expectation value of μ. Some quantum chemical methods only give energies, not wave functions; for those methods the derivative with respect to the field is the only computational access to the dipole moment.
To avoid misunderstanding we reiterate that the Hellman-Feynman theorem holds for exact eigenfunctions, so that the expression for μobs as an expectation value over unperturbed eigenfunctions is true for exact wave functions.
Symmetry
In order to indicate how symmetry can predict the vanishing of a molecular dipole, we consider the first-order formula and space inversion (parity) Π. Parity is a unitary operator. Assume that the non-degenerate zeroth-order wave function has definite (odd or even) parity,
We know, because position vectors change sign, that
Now
where we used that the adjoint Π† of Π, moved to the bra, becomes Π. And finally
This argument can be generalized to arbitrary point groups and leads to the rule: the product of the symmetry species (irreducible representations) of bra, ket, and operator (component of dipole) must contain the totally symmetric representation in order that the expectation value of the operator does not vanish.
Since an atom has inversion symmetry, this reasoning shows that no atom in a non-degenerate state (an S-state, a spherically symmetric state) can have a permanent dipole. In the case of open-shell atoms with degenerate energy levels, one could define a dipole moment by the aid of the first-order Stark effect. This only gives a non-vanishing dipole (by definition proportional to a non-vanishing first-order Stark shift) if some of the wave functions belonging to the degenerate energies have opposite parity; i.e., have different behavior under inversion. This is a rare occurrence, but happens for the first-excited H-atom, where 2s and 2p states are "accidentally" degenerate and have opposite parity (2s is even and 2p is odd).