Inverse trigonometric function: Difference between revisions
imported>Dmitrii Kouznetsov m (misprint) |
imported>Meg Taylor No edit summary |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:AcomapT.png|500px|right|thumb| [[ | {{subpages}} | ||
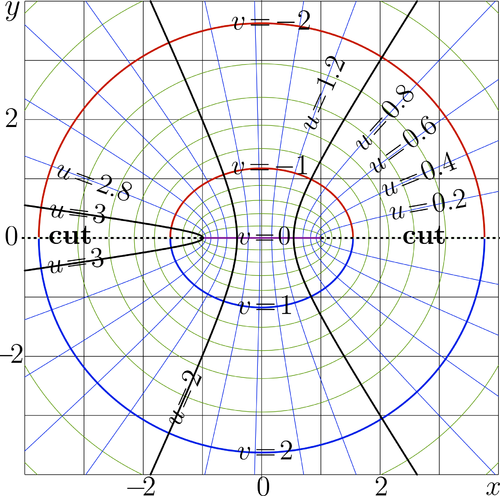
[[File:AcomapT.png|500px|right|thumb| [[Complex map]] of [[ArcCos]] function, <math>u\!+\!iv\!=\!\arccos(i\!+\!iy)</math>]] | |||
'''Inverse trigonometric functions''' are [[ArcSin]], [[ArcCos]], [[ArcTan]] and [[ArcCot]]. | '''Inverse trigonometric functions''' are [[ArcSin]], [[ArcCos]], [[ArcTan]] and [[ArcCot]]. | ||
| Line 6: | Line 7: | ||
==Notations== | ==Notations== | ||
The name of the inverse function is created adding the prefix [[Arc]] to the name of the function. Such a rule is valid for the | The name of the inverse function is created adding the prefix [[Arc]] to the name of the function. Such a rule is valid for the | ||
[[Mathematica]] software. | [[Mathematica]] software. | ||
| Line 17: | Line 17: | ||
==Implementation of the inverse trigonometric functions== | ==Implementation of the inverse trigonometric functions== | ||
Some compilers do not recognize the inverse trigonometric functions of the complex argument. In this case, the representations through function [[Logarithm]] can be used. | |||
Some | |||
For example, [[ArcCos]] can be implemented in in [[C++]] in the following way: | For example, [[ArcCos]] can be implemented in in [[C++]] in the following way: | ||
z_type acos(z_type z){ | z_type acos(z_type z){ | ||
| Line 26: | Line 25: | ||
else {return -I*log( z - sqrt(z*z-1.) );} } | else {return -I*log( z - sqrt(z*z-1.) );} } | ||
, where | , where | ||
"z_type" means "[[complex]]" or "[[complex double]]", | "z_type" means "[[complex]]" or "[[complex double]]", and | ||
"Re" means [[Real part]], and | "Re" means [[Real part]], and | ||
"Im" means [[Imaginary part]]. | "Im" means [[Imaginary part]], and<br> | ||
"I" means z_type(0.,1.) is <math>i=\sqrt{-1}</math>. | |||
This implementation is used to plot the [[Complex map]] of function [[ArcCos]] in the figure at right. | This implementation is used to plot the [[Complex map]] of function [[ArcCos]] in the figure at right. | ||
==Cut lines== | ==Cut lines== | ||
The inverse trigonometric functions are [[holomorphic functions|holomorphic]] in the whole complex plane except unavoidable cut lines; the choice of these cut lines is important for the unambiguity of the result of the application. | The inverse trigonometric functions are [[holomorphic functions|holomorphic]] in the whole complex plane except unavoidable cut lines; the choice of these cut lines is important for the unambiguity of the result of the application. | ||
Latest revision as of 08:25, 10 October 2013
Inverse trigonometric functions are ArcSin, ArcCos, ArcTan and ArcCot.
They are inverse functions of Sin, Cos, Tan and Cot
Notations
The name of the inverse function is created adding the prefix Arc to the name of the function. Such a rule is valid for the Mathematica software.
In Latex the prefix is "arc".
In some programming languages, it is sufficient to add the one prefix "a" to get name of the inverse trigonometric function.
In such a way they are implemented in C++, the functions are called asin, acos, atan.
Implementation of the inverse trigonometric functions
Some compilers do not recognize the inverse trigonometric functions of the complex argument. In this case, the representations through function Logarithm can be used. For example, ArcCos can be implemented in in C++ in the following way:
z_type acos(z_type z){
if(Im(z)<0){if(Re(z)>=0){return I*log( z + sqrt(z*z-1.) );}
else{return I*log( z - sqrt(z*z-1.) );}}
if(Re(z)>=0){return -I*log( z + sqrt(z*z-1.) );}
else {return -I*log( z - sqrt(z*z-1.) );} }
, where
"z_type" means "complex" or "complex double", and
"Re" means Real part, and
"Im" means Imaginary part, and
"I" means z_type(0.,1.) is .
This implementation is used to plot the Complex map of function ArcCos in the figure at right.
Cut lines
The inverse trigonometric functions are holomorphic in the whole complex plane except unavoidable cut lines; the choice of these cut lines is important for the unambiguity of the result of the application.