Separative Work Units (SWUs): Difference between revisions
(→Examples: simplify units of energy to just kW hours) |
mNo edit summary |
||
| (35 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Separative | {{subpages}} | ||
{{TOC|right}} | |||
'''Separative Work Units (SWUs)''' are the measure of "work" done in separating the [[isotope]]s of [[uranium]]. SWUs are NOT units of ''energy'', but rather a measure of ''services'' provided by an enrichment plant. This "bizarre unit", introduced by Paul Dirac in 1941,<ref name=Bernstein/> is ''proportional'' to the amount of energy or time spent, and to the total mass processed. Thus it is useful in setting the price of enrichment services. | |||
Gaseous diffusion plants (such as the original at ORNL<ref name=ORNL/> ) typically require 2,400 to 2,500 kW hours of electricity per SWU, while gas centrifuge plants require just 50 kWh per SWU.<ref>These figures are from the [https://en.wikipedia.org/wiki/Separative_work_units Wikipedia article] which has only a "citation needed" note.</ref> The average price of uranium enrichment in 2023 was $106.97 per SWU, up 6% from $101.03 in 2022.<ref name=price/> | |||
== Calculation == | |||
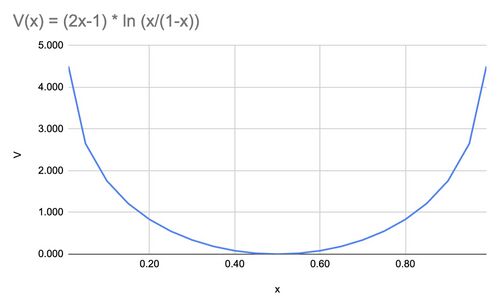
{{Image|SWUfunction.jpg|right|500px|Fig.1 Logarithmic function used in calculating Separative Work Units.}} | |||
SWUs are a function of the assays <ref>fraction of the total uranium content that is U-235</ref> of the feedstock, the enriched product, and the leftover depleted tailings. | |||
The work <math>W_\mathrm{SWU}</math> necessary to separate a mass <ref>Mass is normally in kilograms, but their are other definitions.</ref> <math>F</math> of feed of assay <math>x_{f}</math> into a mass <math>P</math> of product assay <math>x_{p}</math>, and tails of mass <math>T</math> and assay <math>x_{t}</math> is given by the expression: <ref name=Fuchs/> | |||
The work <math>W_\mathrm{SWU}</math> necessary to separate a mass <math>F</math> of feed of assay <math>x_{f}</math> into a mass <math>P</math> of product assay <math>x_{p}</math>, and tails of mass <math>T</math> and assay <math>x_{t}</math> is given by the expression:<ref | |||
:<math>W_\mathrm{SWU} = P \cdot V\left(x_{p}\right)+T \cdot V(x_{t})-F \cdot V(x_{f})</math> | :<math>W_\mathrm{SWU} = P \cdot V\left(x_{p}\right)+T \cdot V(x_{t})-F \cdot V(x_{f})</math> | ||
where <math>V | where <math>V(x)</math> is the ''value function'', defined as: <ref name=Bernstein/> | ||
:<math>V(x) = (2x - 1) \ln \left(\frac{x}{1 - x}\right)</math> | :<math>V(x) = (2x - 1) \ln \left(\frac{x}{1 - x}\right)</math> | ||
Given the desired amount of product <math>P</math>, the necessary feed <math>F</math> and resulting tails <math>T</math> are: | |||
:<math>F = \frac{x_{p} - x_{t}}{x_{f} - x_{t}} \cdot P</math> | |||
:<math>\frac{ | :<math>T = \frac{x_{p} - x_{f}}{x_{f} - x_{t}} \cdot P</math> | ||
== Examples == | == Examples == | ||
To produce 10 kg of Low Enriched Uranium (LEU) with U-235 content at 4.5%, and a tails assay of 0.3%, you will need 105 kg of natural uranium (NU) 0.7% and 63 SWU of enrichment services. | |||
A large nuclear power station with a net electrical capacity of 1300 MW requires about 25 tonnes per year of LEU with a U-235 concentration of 3.75%. This quantity is produced from about 210 tonnes of NU using about 120,000 SWU. An enrichment plant with a capacity of 1 million SWU per year can enrich the uranium needed to fuel about eight large nuclear power stations. | |||
Assuming the cost of bomb-grade highly-enriched uranium (HEU: 90% U-235) starting from natural uranium (NU: 0.7% U-235) is just the cost of enrichment ($100 per SWU) 5 kg of HEU will cost $115K. Starting from 20% U-235 the cost would be $10K. | |||
For more examples see [https://docs.google.com/spreadsheets/d/1OyKPyjo6k1ckZVwAh8sfkDEtB5W22VUriBaelK3LWY4/edit?gid=0#gid=0 Uranium Enrichment / Separative Work Units] These examples are relevant to the question - Will worldwide distribution of MEU (Moderately Enriched Uranium, 20% U-235, or HALEU to use | For more examples see [https://docs.google.com/spreadsheets/d/1OyKPyjo6k1ckZVwAh8sfkDEtB5W22VUriBaelK3LWY4/edit?gid=0#gid=0 Uranium Enrichment / Separative Work Units] These examples are relevant to the question - Will worldwide distribution of MEU-20 (Moderately Enriched Uranium, 20% U-235, or HALEU<ref>This monstrous backronym means "High Assay Low Enriched Uranium"</ref> to use industry jargon) will this massive production and shipment of fissile material be an easy target for the Bad Guys? | ||
''Note for Wannabe Bomb Makers:''<br> | ''Note for Wannabe Bomb Makers:''<br> | ||
Enriching uranium is very difficult. To get above 90% (weapons grade) it takes a lot of "work" by the centrifuges. The work increases asymptotically as you approach 100% (see Figure 1). It is also difficult starting with natural uranium (0.7%). Centrifuges work best with a 50/50 mixture of isotopes. If you can steal some 20% from a nearby power plant with a "new generation" reactor, it will be a bit easier than starting with 5%, which is the best you can find in an "old generation" power plant. | Enriching uranium is very difficult. To get above 90% (weapons grade) it takes a lot of "work" by the centrifuges. The work increases asymptotically as you approach 100% (see Figure 1). It is also difficult starting with natural uranium (0.7%). Centrifuges work best with a 50/50 mixture of isotopes. If you can steal some 20% from a nearby power plant with a "new generation" reactor, it will be a bit easier than starting with 5%, which is the best you can find in an "old generation" power plant. | ||
== References == | ==Attribution== | ||
< | Some content on this page may previously have appeared on Wikipedia; see it's article on [[Wikipedia:separative work units|Separative work units]] for more details. | ||
== Notes and References == | |||
{{Reflist|refs= | |||
<ref name=Bernstein> Bernstein, J. (2009). ''SWU for You and Me''. [https://arxiv.org/abs/0906.2505 arXiv:0906.2505] has an interesting history of centrifuges and the derivation of the SWU unit. | |||
</ref> | |||
{{cite arXiv|last=Bernstein|first=Jeremy|date=2009-06-13|title=SWU for You and Me|class=physics.hist-ph|eprint=0906.2505}} | |||
[[Category: | <ref name=Fuchs> {{cite book|last=Fuchs|first=K.|title=Selected Scientific Papers Of Sir Rudolf Peierls, With Commentary By The Author|publisher=World Scientific Publishing Company|year=1997|isbn=9789814498883}} | ||
</ref> | |||
<ref name=ORNL>See Wikipedia's article on [[Wikipedia:Oak Ridge National Laboratory|Oak Ridge National Laboratory]] (ORNL) for more information. | |||
</ref> | |||
<ref name=price> {{cite web |title=Uranium Marketing Annual Report |url=https://www.eia.gov/uranium/marketing/ |website=eia.gov |publisher=US Energy Information Administration }} accessed 28 July 2024. | |||
</ref> | |||
}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 06:01, 17 October 2024
Separative Work Units (SWUs) are the measure of "work" done in separating the isotopes of uranium. SWUs are NOT units of energy, but rather a measure of services provided by an enrichment plant. This "bizarre unit", introduced by Paul Dirac in 1941,[1] is proportional to the amount of energy or time spent, and to the total mass processed. Thus it is useful in setting the price of enrichment services.
Gaseous diffusion plants (such as the original at ORNL[2] ) typically require 2,400 to 2,500 kW hours of electricity per SWU, while gas centrifuge plants require just 50 kWh per SWU.[3] The average price of uranium enrichment in 2023 was $106.97 per SWU, up 6% from $101.03 in 2022.[4]
Calculation
SWUs are a function of the assays [5] of the feedstock, the enriched product, and the leftover depleted tailings.
The work Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_\mathrm{SWU}} necessary to separate a mass [6] Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} of feed of assay Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{f}} into a mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} of product assay Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{p}} , and tails of mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} and assay Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{t}} is given by the expression: [7]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_\mathrm{SWU} = P \cdot V\left(x_{p}\right)+T \cdot V(x_{t})-F \cdot V(x_{f})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)} is the value function, defined as: [1]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x) = (2x - 1) \ln \left(\frac{x}{1 - x}\right)}
Given the desired amount of product Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} , the necessary feed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} and resulting tails Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} are:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \frac{x_{p} - x_{t}}{x_{f} - x_{t}} \cdot P}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = \frac{x_{p} - x_{f}}{x_{f} - x_{t}} \cdot P}
Examples
To produce 10 kg of Low Enriched Uranium (LEU) with U-235 content at 4.5%, and a tails assay of 0.3%, you will need 105 kg of natural uranium (NU) 0.7% and 63 SWU of enrichment services.
A large nuclear power station with a net electrical capacity of 1300 MW requires about 25 tonnes per year of LEU with a U-235 concentration of 3.75%. This quantity is produced from about 210 tonnes of NU using about 120,000 SWU. An enrichment plant with a capacity of 1 million SWU per year can enrich the uranium needed to fuel about eight large nuclear power stations.
Assuming the cost of bomb-grade highly-enriched uranium (HEU: 90% U-235) starting from natural uranium (NU: 0.7% U-235) is just the cost of enrichment ($100 per SWU) 5 kg of HEU will cost $115K. Starting from 20% U-235 the cost would be $10K.
For more examples see Uranium Enrichment / Separative Work Units These examples are relevant to the question - Will worldwide distribution of MEU-20 (Moderately Enriched Uranium, 20% U-235, or HALEU[8] to use industry jargon) will this massive production and shipment of fissile material be an easy target for the Bad Guys?
Note for Wannabe Bomb Makers:
Enriching uranium is very difficult. To get above 90% (weapons grade) it takes a lot of "work" by the centrifuges. The work increases asymptotically as you approach 100% (see Figure 1). It is also difficult starting with natural uranium (0.7%). Centrifuges work best with a 50/50 mixture of isotopes. If you can steal some 20% from a nearby power plant with a "new generation" reactor, it will be a bit easier than starting with 5%, which is the best you can find in an "old generation" power plant.
Attribution
Some content on this page may previously have appeared on Wikipedia; see it's article on Separative work units for more details.
Notes and References
- ↑ 1.0 1.1 Bernstein, J. (2009). SWU for You and Me. arXiv:0906.2505 has an interesting history of centrifuges and the derivation of the SWU unit.
- ↑ See Wikipedia's article on Oak Ridge National Laboratory (ORNL) for more information.
- ↑ These figures are from the Wikipedia article which has only a "citation needed" note.
- ↑ Uranium Marketing Annual Report. US Energy Information Administration. accessed 28 July 2024.
- ↑ fraction of the total uranium content that is U-235
- ↑ Mass is normally in kilograms, but their are other definitions.
- ↑ Fuchs, K. (1997). Selected Scientific Papers Of Sir Rudolf Peierls, With Commentary By The Author. World Scientific Publishing Company. ISBN 9789814498883.
- ↑ This monstrous backronym means "High Assay Low Enriched Uranium"