Series (mathematics): Difference between revisions
imported>Aleksander Stos (→Motivations and examples: more) |
imported>Aleksander Stos |
||
| Line 20: | Line 20: | ||
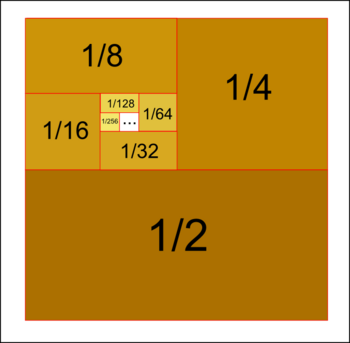
Instead of a rigorous proof, we present a picture (see fig.1) which gives a geometric interpretation. Each term is represented by a rectangle of the corresponding area. At any moment (given any number of rectangular "chips on the table"), the next rectangle covers exactly one half of the remaining space. Thus, the chips will never cover more than the unit square. In other words, the sum increases when more terms are added, but it does not go to the infinity, it never exceeds 1. The series ''converges''.<ref>A simple calculation shows that the sum is actually equal to one.</ref> | Instead of a rigorous proof, we present a picture (see fig.1) which gives a geometric interpretation. Each term is represented by a rectangle of the corresponding area. At any moment (given any number of rectangular "chips on the table"), the next rectangle covers exactly one half of the remaining space. Thus, the chips will never cover more than the unit square. In other words, the sum increases when more terms are added, but it does not go to the infinity, it never exceeds 1. The series ''converges''.<ref>A simple calculation shows that the sum is actually equal to one.</ref> | ||
One may think that any decreasing sequence would eventually lead to a convergent series. This, however, is not the case. Consider for example the series<ref>It is often called harmonic series</ref> | One may tend to think that any decreasing sequence would eventually lead to a convergent series. This, however, is not the case. Consider for example the series<ref>It is often called harmonic series</ref> | ||
:<math> 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\ldots</math> | :<math> 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\ldots</math> | ||
To see that it diverges to infinity, let us make the following groups of terms (we may forget the one at the beginning): | To see that it diverges to infinity, let us make the following groups of terms (we may forget the one at the beginning): | ||
Revision as of 11:33, 30 May 2007
In mathematics, a series is the cumulative sum of a given sequence of terms. Typically, these terms are real or complex numbers, but much more generality is possible.
For example, given the sequence of the natural numbers 1, 2, 3, ..., the series is 1, 1 + 2, 1 + 2 + 3, ...
According to the number of terms, the series may be finite or infinite. The former is relatively easy to deal with. In fact, the finite series is identified with the sum of all terms and — apart from the elementary algebra — there is no particular theory that applies. It turns out, however, that much care is required when manipulating infinite series. For example, some simple operations borrowed from elementary algebra — such as a change of order of the terms often lead to unexpected results. So it is sometimes tacitly understood, especially in analysis, that the term "series" refers to the infinite series. In what follows we adopt this convention and concentrate on the theory of the infinite case.
Motivations and examples
Given a series, an obvious question arises. Does it make sense to talk about the sum of all terms? Clearly, it is not always the case. Consider a simple example when the general term is constant and equal to 1, say. That is, the series reads as
- 1,
- 2=1+1,
- 3=1+1+1,
- 4=1+1+1+1,
...etc. One observes that the sum of all terms can not be finite. In mathematical language, the series diverges to infinity. [1] There is not much to say about such an object. If we want to build an interesting theory, that is to have some examples, operations and theorems, we need to deal with convergent series, that is series for which the sum of all terms is well-defined.
Actually, are there any? Maybe any series would diverge like this? Consider the following series of decreasing terms
This is a special example of what is called geometric series. The sum is finite! Instead of a rigorous proof, we present a picture (see fig.1) which gives a geometric interpretation. Each term is represented by a rectangle of the corresponding area. At any moment (given any number of rectangular "chips on the table"), the next rectangle covers exactly one half of the remaining space. Thus, the chips will never cover more than the unit square. In other words, the sum increases when more terms are added, but it does not go to the infinity, it never exceeds 1. The series converges.[2]
One may tend to think that any decreasing sequence would eventually lead to a convergent series. This, however, is not the case. Consider for example the series[3]
To see that it diverges to infinity, let us make the following groups of terms (we may forget the one at the beginning):
- 1/2,
- 1/3+1/4,
- 1/5+1/6+1/7+1/8,
- 1/9+1/10+1/11+1/12+1/13+1/14+1/15+1/16,
etc. Notice that each group ends by a term of the form the smallest one in the group. Note also that group that ends by has two members, the one that ends by has four members and so on. Generally, a group that ends by has terms, each of which is greater than the smallest one at the end. So if we pick a group and replace each term by the smallest one, we would get that the sum of the group is greater than
- members (this is the smallest term).
It follows that the sum of each group is greater than one half! And since there are infinitely many of such groups, the sum of all terms is not finite.
These examples show that we need a criteria to decide whether a given series is convergent. Before such a tool can be developed we need some mathematical notation.
Formal definition
Given a sequence of elements that can be added, let
Then, the series is defined as the sequence and denoted by [4] For a single n, the sum is called the partial sum of the series.
If the sequence has a finite limit, the series is said to be convergent. In this case we define the sum of the series as
Note that the sum (i.e. the numeric value of the above limit) and the series (i.e. the sequence ) are usually denoted by the same symbol. If the above limit does not exist - or is infinite - the series is said to be divergent.