Pythagorean theorem: Difference between revisions
Jump to navigation
Jump to search

imported>Subpagination Bot m (Add {{subpages}} and remove any categories (details)) |
imported>Yitzchak Novick No edit summary |
||
| Line 4: | Line 4: | ||
In [[Euclidean geometry]], the '''Pythagorean theorem''' states that: | In [[Euclidean geometry]], the '''Pythagorean theorem''' states that: | ||
:: The sum of the areas of the squares on the legs of a [[right triangle]] | :: The sum of the areas of the squares on the legs of a [[right triangle]] is equal to the area of the square on the [[hypotenuse]]. | ||
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle. | The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle. | ||
The Pythagorean theorem is commonly known by its algebraic notation: | |||
a² + b² = c² | |||
where a and b are the lengths of the two legs of the right triangle and c is the length of the hypotenuse. | |||
Revision as of 10:20, 11 July 2008

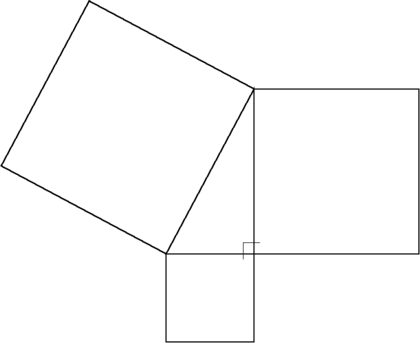
The Pythagorean theorem: The sum of the areas of the two squares on the legs (the sides that meet at a right angle) equals the area of the square on the hypotenuse (the side opposite the right angle).
In Euclidean geometry, the Pythagorean theorem states that:
- The sum of the areas of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle.
The Pythagorean theorem is commonly known by its algebraic notation:
a² + b² = c²
where a and b are the lengths of the two legs of the right triangle and c is the length of the hypotenuse.