Vector product: Difference between revisions
imported>Paul Wormer (Even more explicit reference to cross product) |
imported>Paul Wormer (Moved text cross product to heading vector product + some rewrite) |
||
| Line 1: | Line 1: | ||
A '''vector product''' is an antisymmetric product of two vectors in 3-dimensional Euclidean space <math>\scriptstyle \mathbb{R}^3</math>. | A '''vector product''', also known as '''cross product''', is an antisymmetric product '''A''' × '''B''' = −'''B''' × '''A''' of two vectors '''A''' and '''B''' in 3-dimensional Euclidean space <math>\scriptstyle \mathbb{R}^3</math>. The vector product is again a 3-dimensional vector. The vector product is widely used in many areas of mathematics, mechanics, electromagnetism, gravitational fields, etc. | ||
=== Definition === | |||
Given two vectors, '''A''' and '''B''' in <math>\scriptstyle \mathbb{R}^3</math>, the vector product is a vector with length ''AB'' sin θ<sub>AB</sub>, where ''A'' is the length of '''A''', ''B'' is the length of '''B''', and θ<sub>AB</sub> is the smaller angle between '''A''' and '''B'''. The direction of the vector product is perpendicular (or normal to) the plane containing the vectors '''A''' and '''B''' and follows the right-hand rule (see below), | |||
: '''A''' × '''B''' = '''a'''<sub>N</sub> |'''A'''| |'''B'''| sinθ<sub>AB</sub>, | |||
where '''a'''<sub>N</sub> is a unit vector normal to the plane spanned by '''A''' and '''B''' in the right-hand rule direction. | |||
We recall that the length of a vector is the square root of the [[dot product]] of a vector with itself, ''A'' ≡ |'''A'''| = ('''A''' ⋅ '''A''' )<sup>1/2</sup> and similarly for the length of '''B'''. | |||
From the antisymmetry '''A''' × '''B''' = −'''B''' × '''A''' follows that the cross (vector) product of any vector with itself (or another parallel or antiparallel vector) is zero because '''A''' × '''A''' = − '''A''' × '''A''' and the only quantity equal to minus itself is the zero. Alternatively, one may derive this from the fact that sin(0) = 0 (parallel vectors) and sin(180) = 0 (antiparallel vectors). | |||
=== Another formulation === | |||
Rather than from the angle and perpendicular unit vector, the form of the cross product below is often used. In this definition we need to express the vectors with respect to a Cartesian (orthonormal) coordinate frame '''a'''<sub>x</sub>, '''a'''<sub>y</sub> and '''a'''<sub>z</sub> of <math>\scriptstyle \mathbb{R}^3</math>. With respect to this frame we write '''A''' = (A<sub>x</sub>, A<sub>y</sub>, A<sub>z</sub>) and '''B''' = (B<sub>x</sub>, B<sub>y</sub>, B<sub>z</sub>). Then | |||
'''A''' × '''B''' = (A<sub>y</sub>B<sub>z</sub> - A<sub>z</sub>B<sub>y</sub>)<b>a</b><sub>x</sub> + (A<sub>z</sub>B<sub>x</sub> - A<sub>x</sub>B<sub>z</sub>)<b>a</b><sub>y</sub> + (A<sub>x</sub>B<sub>y</sub> - A<sub>y</sub>B<sub>x</sub>)<b>a</b><sub>z</sub>, | |||
This formula can be written more concisely upon introduction of a [[determinant]]: | |||
<math> | |||
\mathbf A \times \mathbf B = | |||
\left|\begin{array}{ccc} \mathbf a_x & \mathbf a_y & \mathbf a_z \\ | |||
A_x & A_y & A_z \\ | |||
B_x & B_y & B_z \end{array} \right|, | |||
</math> | |||
where <math>\left|\cdot\right|</math> denotes the determinant of a matrix. | |||
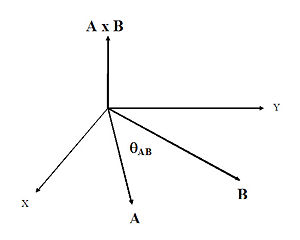
[[Image:CrossProduct.jpg|right|300px|thumb|Diagram illustrating the direction of '''A'''×'''B''']] | |||
== The right hand rule == | |||
The diagram on the right illustrates the direction of '''A''' × '''B''', which follows the right hand rule. If one points the fingers of the right hand towards the head of vector '''A''' (with the wrist at the origin), then curls them towards the direction of '''B''', the extended thumb will point in the direction of '''A''' × '''B'''. | |||
==Generalization== | |||
From a somewhat more abstract point of view one may define the vector product as an element of the antisymmetric subspace of the 9-dimensional tensorproduct space <math>\scriptstyle \mathbb{R}^3 \otimes \mathbb{R}^3 </math>. This antisymmetric subspace is of dimension 3. | |||
In general the antisymmetric subspace of the ''k''-fold tensor power <math>\scriptstyle \mathbb{R}^n \otimes \mathbb{R}^n\otimes \cdots\otimes\mathbb{R}^n </math> is of dimension <math>\scriptstyle {n \choose k}</math>. Elements of such space are often called [[wedge products]] written as | |||
:<math> | |||
A_1 \wedge A_2 \wedge A_3 \cdots \wedge A_k. | |||
</math> | |||
The antisymmetric subspace of a two-fold tensor product is of dimension <math>\scriptstyle {n \choose 2} = n(n-1)/2</math>. The latter number is equal to 3 only if ''n'' = 3. For instance, for ''n'' = 2 or 4, the antisymmetric subspaces are of dimension 1 and 6, respectively. If one regards the cross product in <math>\scriptstyle \mathbb{R}^3</math> from the point of view of antisymmetric subspaces, it is a coincidence that it lies again in <math>\scriptstyle \mathbb{R}^3</math>. | |||
And indeed, the cross product lacks the property of a vector that it changes sign under inversion [both factors of the cross product change sign and (−1)×(−1) = 1]. A vector that does not change sign under inversion is called an [[axial vector]] or [[pseudo vector]]. Hence a cross product is a pseudo vector. A vector that does change sign is in this context often referred to as a [[polar vector]]. | |||
[[Category:CZ Live]] | |||
[[Category:Physics Workgroup]] | |||
[[Category:Mathematics Workgroup]] | |||
[[Category: CZ Live]] | [[Category: CZ Live]] | ||
[[Category: Mathematics Workgroup]] | [[Category: Mathematics Workgroup]] | ||
[[Category: Physics Workgroup]] | [[Category: Physics Workgroup]] | ||
Revision as of 04:58, 5 January 2008
A vector product, also known as cross product, is an antisymmetric product A × B = −B × A of two vectors A and B in 3-dimensional Euclidean space . The vector product is again a 3-dimensional vector. The vector product is widely used in many areas of mathematics, mechanics, electromagnetism, gravitational fields, etc.
Definition
Given two vectors, A and B in , the vector product is a vector with length AB sin θAB, where A is the length of A, B is the length of B, and θAB is the smaller angle between A and B. The direction of the vector product is perpendicular (or normal to) the plane containing the vectors A and B and follows the right-hand rule (see below),
- A × B = aN |A| |B| sinθAB,
where aN is a unit vector normal to the plane spanned by A and B in the right-hand rule direction.
We recall that the length of a vector is the square root of the dot product of a vector with itself, A ≡ |A| = (A ⋅ A )1/2 and similarly for the length of B.
From the antisymmetry A × B = −B × A follows that the cross (vector) product of any vector with itself (or another parallel or antiparallel vector) is zero because A × A = − A × A and the only quantity equal to minus itself is the zero. Alternatively, one may derive this from the fact that sin(0) = 0 (parallel vectors) and sin(180) = 0 (antiparallel vectors).
Another formulation
Rather than from the angle and perpendicular unit vector, the form of the cross product below is often used. In this definition we need to express the vectors with respect to a Cartesian (orthonormal) coordinate frame ax, ay and az of . With respect to this frame we write A = (Ax, Ay, Az) and B = (Bx, By, Bz). Then
A × B = (AyBz - AzBy)ax + (AzBx - AxBz)ay + (AxBy - AyBx)az,
This formula can be written more concisely upon introduction of a determinant:
where denotes the determinant of a matrix.
The right hand rule
The diagram on the right illustrates the direction of A × B, which follows the right hand rule. If one points the fingers of the right hand towards the head of vector A (with the wrist at the origin), then curls them towards the direction of B, the extended thumb will point in the direction of A × B.
Generalization
From a somewhat more abstract point of view one may define the vector product as an element of the antisymmetric subspace of the 9-dimensional tensorproduct space . This antisymmetric subspace is of dimension 3.
In general the antisymmetric subspace of the k-fold tensor power is of dimension . Elements of such space are often called wedge products written as
The antisymmetric subspace of a two-fold tensor product is of dimension . The latter number is equal to 3 only if n = 3. For instance, for n = 2 or 4, the antisymmetric subspaces are of dimension 1 and 6, respectively. If one regards the cross product in from the point of view of antisymmetric subspaces, it is a coincidence that it lies again in . And indeed, the cross product lacks the property of a vector that it changes sign under inversion [both factors of the cross product change sign and (−1)×(−1) = 1]. A vector that does not change sign under inversion is called an axial vector or pseudo vector. Hence a cross product is a pseudo vector. A vector that does change sign is in this context often referred to as a polar vector.