Hund's rules: Difference between revisions
Jump to navigation
Jump to search
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 3: | Line 3: | ||
A group of atomic energy levels, obtained by [[Russell-Saunders coupling]], is concisely indicated by a [[term symbol]]. As discussed in the article [[Russell-Saunders coupling]], closed shells and closed subshells have ''L'' = ''S'' = 0 and hence can be ignored in the coupling. A ''term'' (also known as ''multiplet'') is a set of simultaneous eigenfunctions of '''L'''<sup>2</sup> (total orbital angular momentum squared) and '''S'''<sup>2</sup> (total spin angular momentum squared) with given quantum numbers ''L'' and ''S'', respectively. | A group of atomic energy levels, obtained by [[Russell-Saunders coupling]], is concisely indicated by a [[term symbol]]. As discussed in the article [[Russell-Saunders coupling]], closed shells and closed subshells have ''L'' = ''S'' = 0 and hence can be ignored in the coupling. A ''term'' (also known as ''multiplet'') is a set of simultaneous eigenfunctions of '''L'''<sup>2</sup> (total orbital angular momentum squared) and '''S'''<sup>2</sup> (total spin angular momentum squared) with given quantum numbers ''L'' and ''S'', respectively. | ||
If there is no spin-orbit coupling, the functions of one term (fixed ''L'' and ''S'') are degenerate (have the same energy). If there is weak spin-orbit coupling it is useful to diagonalize the matrix of the corresponding spin-orbit operator within the ''LS'' basis in the spirit of first-order [[perturbation theory]]. This introduces the new quantum number ''J'', with |''L''-''S''| ≤ ''J'' ≤ ''L''+''S'', that labels a 2(''J''+1)-dimensional energy level. | If there is no spin-orbit coupling, the functions of one term (fixed ''L'' and ''S'') are degenerate (have the same energy). If there is weak spin-orbit coupling it is useful to diagonalize the matrix of the corresponding spin-orbit operator within the ''LS'' basis in the spirit of first-order [[perturbation theory]]. This introduces the new quantum number ''J'', with |''L''-''S''| ≤ ''J'' ≤ ''L''+''S'', that labels a 2(''J''+1)-dimensional energy level. | ||
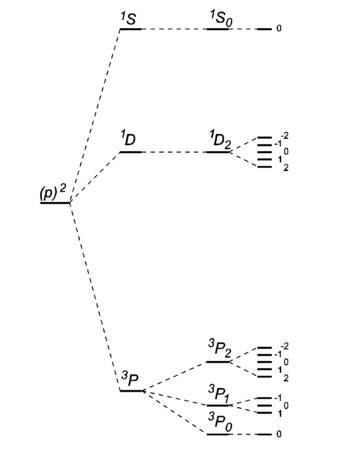
[[Image:Carbon levels.png|right|thumb|350px|Level scheme of the [[carbon]] atom <math>\scriptstyle (1s)^2(2s)^2(2p)^2</math>. Drawing is not on scale. On the left the energy | |||
without any two-particle interaction. Then three-fold energy splitting after switching on electrostatic electron-electron interaction (''L'' and ''S'' good quantum numbers). Then splittings after switching on first-order spin-orbit coupling (''J'' good quantum number). Finally on the right [[Zeeman]] splittings in an external magnetic field.]] | |||
Hund's rules are:<ref>L. Pauling, ''The Nature of the Chemical Bond'', Cornell University Press, Ithaca, 3rd edition (1960)</ref> | Hund's rules are:<ref>L. Pauling, ''The Nature of the Chemical Bond'', Cornell University Press, Ithaca, 3rd edition (1960)</ref> | ||
| Line 23: | Line 27: | ||
^3P_{2} < ^3P_{1} < ^3P_{0} < ^1D_{2} < ^1S_{0}. | ^3P_{2} < ^3P_{1} < ^3P_{0} < ^1D_{2} < ^1S_{0}. | ||
</math> | </math> | ||
==References== | ==References== | ||
Revision as of 10:25, 13 January 2008
In atomic spectroscopy, Hund's rules predict the order of atomic energy levels with quantum numbers L, S and J. The rules are called after Friedrich Hund who formulated them in 1925.[1]
A group of atomic energy levels, obtained by Russell-Saunders coupling, is concisely indicated by a term symbol. As discussed in the article Russell-Saunders coupling, closed shells and closed subshells have L = S = 0 and hence can be ignored in the coupling. A term (also known as multiplet) is a set of simultaneous eigenfunctions of L2 (total orbital angular momentum squared) and S2 (total spin angular momentum squared) with given quantum numbers L and S, respectively.
If there is no spin-orbit coupling, the functions of one term (fixed L and S) are degenerate (have the same energy). If there is weak spin-orbit coupling it is useful to diagonalize the matrix of the corresponding spin-orbit operator within the LS basis in the spirit of first-order perturbation theory. This introduces the new quantum number J, with |L-S| ≤ J ≤ L+S, that labels a 2(J+1)-dimensional energy level.
Level scheme of the carbon atom . Drawing is not on scale. On the left the energy without any two-particle interaction. Then three-fold energy splitting after switching on electrostatic electron-electron interaction (L and S good quantum numbers). Then splittings after switching on first-order spin-orbit coupling (J good quantum number). Finally on the right Zeeman splittings in an external magnetic field.
Hund's rules are:[2]
- Of the Russell-Saunders states arising from a given electronic configuration those with the largest spin quantum number S lie lowest, those with the next largest next, and so on; in other words, the states with largest spin multiplicity are the most stable.
- Of the group of terms with a given value of S, that with the largest value of L lies lowest.
- Of the states with given values of S and L in an electronic configuration consisting of less than half the electrons in a closed subshell, the state with the smallest value of J is usually the most stable, and for a configuration consisting of more than half the electrons in a closed subshell the state with largest J is the most stable.
The levels of the second sort, largest J most stable, can be seen as arising from holes in a closed subshell.
Examples:
- The ground state carbon atom, (1s)2(2s)2(2p)2, gives by Russell-Saunders coupling a set of energy levels labeled by term symbols. Hund's rules predict the following order of the energies:
- The ground state oxygen atom, (1s)2(2s)2(2p)4, (a two-hole state) gives by Russell-Saunders coupling a set of energy levels labeled by term symbols. Hund's rules predict the following order of the energies:
References
- ↑ F. Hund, Zur Deutung verwickelter Spektren, insbesondere der Elemente Scandium bis Nickel. [On the interpretation of complicated spectra, in particular the elements scandium through nickel]. Zeitschrift für Physik, vol. 33, pp. 345-371 (1925).
- ↑ L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 3rd edition (1960)