Tetration: Difference between revisions
imported>Dmitrii Kouznetsov |
imported>Dmitrii Kouznetsov No edit summary |
||
| Line 1: | Line 1: | ||
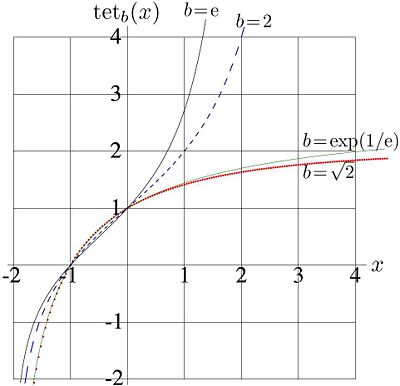
[[Image:TetrationReal.jpg|right| | [[Image:TetrationReal.jpg|right|400px|thumb|Fig.1. Tetration | ||
<math>\mathrm{tet}_b(x)</math> for | <math>\mathrm{tet}_b(x)</math> for | ||
<math>b=\mathrm{e}</math>, | <math>b=\mathrm{e}</math>, | ||
Revision as of 05:36, 29 October 2008
This article is currently under construction. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration
Definiton
For real , Tetration on the base is function of complex variable, which is holomorphic at least in the range , bounded in the range , and satisfies conditions
at least within range .
Real values of the arguments
Examples of behavior of this function at the real axis are shown in figure 1 for values , , , and for . It has logarithmic singularity at , and it is monotonously increasing function.
At tetration approaches its limiting value as , and .
At tetration grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation. A number, that cannot be stored as floating point, could be stored as for some standard value of (for example, or ) and relatively moderate value of . The analytic properties of tetration could be used for the implementation of arithmetic operations without to convert numbers to the floating point representation.
Integer values of the argument
For integer , tetration
Etymology
Creation of word tetration is attributed to Englidh mathematician Reuben Louis Goodstein [1] [2].
Piecewice tetration
uxp
Analytic tetration
This section is not yet written. There is non-finished draft at User:Dmitrii Kouznetsov/Analytic Tetration.
Inverse of tetration
See also
References
- ↑ "TETRATION, a term for repeated exponentiation, was introduced by Reuben Louis Goodstein". Earliest Known Uses of Some of the Words of Mathematics, http://members.aol.com/jeff570/t.html
- ↑ R.L.Goodstein (1947). "Transfinite ordinals in recursive number theory". Journal of Symbolic Logic 12.
Free online sources
- http://reglos.de/lars/ffx.html , Lars Kindermann. References about Iterative Roots and Fractional Iteration.
- http://math.eretrandre.org/tetrationforum/index.php , Discussion about tetration
- http://tetration.itgo.com/ Tetration site by Andrew Robbins
- http://www.tetration.org/ Tetration site by Daniel Geisler