Right-hand rule: Difference between revisions
Jump to navigation
Jump to search

imported>Paul Wormer (New page: {{subpages}} right|thumb|350px|Right-hand rule. Move open palm of right hand from ''x'' to ''y'', then thumb is direction of ''z''. The '''right-hand...) |
imported>Paul Wormer No edit summary |
||
| Line 6: | Line 6: | ||
</math> | </math> | ||
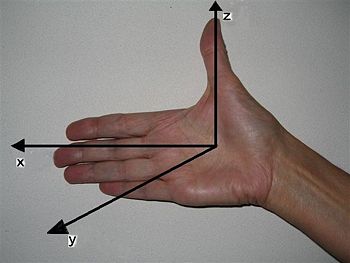
The direction of the unit vector '''e'''<sub>z</sub> given as the cross product of unit vectors along the ''x''- and ''y''-axis is given by the right-hand rule, see photograph. | The direction of the unit vector '''e'''<sub>z</sub> given as the cross product of unit vectors along the ''x''- and ''y''-axis is given by the right-hand rule, see photograph. | ||
The case depicted here has a right (90° degree) angle α between the ''x''- and the ''y''-axis. However, the rule works for ''any'' angle α between ''x''- and ''y''-axis, as long as 0° < α ≤ 180°. The ''z''-axis is always perpendicular to the plane containing the ''x''- and ''y''-axes. | |||
Revision as of 07:53, 7 July 2008
The right-hand rule is a rule that appears in the cross product,
The direction of the unit vector ez given as the cross product of unit vectors along the x- and y-axis is given by the right-hand rule, see photograph.
The case depicted here has a right (90° degree) angle α between the x- and the y-axis. However, the rule works for any angle α between x- and y-axis, as long as 0° < α ≤ 180°. The z-axis is always perpendicular to the plane containing the x- and y-axes.