User talk:Paul Wormer/scratchbook

The second law of thermodynamics, as formulated in the middle of the 19th century by William Thomson (Lord Kelvin) and Rudolf Clausius, states that it is impossible to gain mechanical energy from heat flowing from a cold to a hot body. Clausius postulated that the opposite is the case, namely, that it always requires input of mechanical energy (work) to transport heat from a low- to a high-temperature object.

Thomson formulated the principle in a slightly different, but equivalent way. He said that it is impossible to extract work from a single source of heat in a cyclic process. In a cyclic process the heat source finishes in an thermodynamic state that is identical to the state at the beginning of the process; the heat source does not lose any net internal energy. In order that a cyclic process is in agreement with the first law of thermodynamics (i.e., conserves energy), it is necessary that the heat generated by the work is returned to the heat source.

Without the second law there would be no energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to propel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When one could extract a small portion of it—whereby a slight cooling of the sea water would occur—and use this energy to propel a ship (a form of work), then ships could move without any net consumption of energy. It would not violate the first law of thermodynamics, because the ship's rotating propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, it is not possible, no work can be extracted from the water, because it is a single source of heat. Clausius would explain the impossibility by observing that ships are warmer than sea water (or at least they are not colder) and hence it needs work to transport heat from the sea to the ship.

PD Image
Fig. 1. Second law: If W > 0 then T₁ > T₂ and Q_out ≠ 0.

A similar setup on land, where energy extracted from the earth, would charge batteries, and heat, dissipated by electric currents generated by the batteries, would be given back to the earth, is also out of the question because of the same fundamental law.

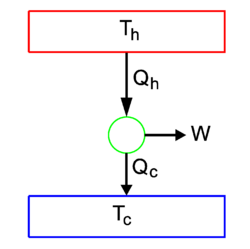
The second law is summarized in figure 1. Two heat reservoirs are shown, one of absolute temperature T₁ and the other of temperature T₂. They are coupled by a heat engine (green circle), a construct that can convert heat Q_in into work W. The "rest heat" Q_out is delivered to reservoir 2.

The scheme shown in figure 1, invented by Sadi Carnot, is an idealized representation of many power-generating machines. Take for instance, an ordinary motor car. The first heat bath is formed by the cylinders in which gasoline is burned, the second heat bath is the environment of the car—the rest heat is delivered to it through the car's radiator. The heat engine is formed by the moving pistons that perform the actual work.

When net work W (positive) is performed, the Kelvin principle states that Q_out ≠ 0, because otherwise there would be a single heat source. The Clausius principle states that necessarily T₁ > T₂. Hence the second law states that it is not possible to convert all the heat Q_in delivered by the first reservoir into work, part of it goes into rest heat Q_out that is transported to a second reservoir of lower temperature. In the case of a car it means that only part of the combustion energy of the gasoline is converted into work, and that a running car by necessity heats up its environment.

It can be derived that the efficiency η ≡ W / Q_in has the maximum

$\eta \leq {\frac {T_{1}-T_{2}}{T_{1}}}.$

Thus, when the car cylinders operate at 500 °C ≈ 800 K and the environment is about 300 K, then η ≤ 500/800 = 62%. It is important to note that this efficiency is a consequence of the second law of thermodynamics, and can only be raised by higher T₁ not by a better streamline or other design improvements.

Mathematical expression of the second law

Let DQ be a small amount of heat entering or leaving a system in a reversible (quasistatic) manner and let T be the absolute temperature of the system. In the article entropy it is proved from the Clausius/Kelvin principle that the quantity dS defined by

$dS\;{\stackrel {\mathrm {def} }{=}}\;{\frac {DQ}{T}}$

is the differential of a state variable S, the entropy of the system. The fact that S is a state function implies that the following holds for a reversible cyclic process, where the suffix "rev" is added to stress that this law holds only for reversible processes,

$\oint {\frac {DQ_{\mathrm {rev} }}{T}}\equiv {\int \limits _{1}\limits ^{2}}_{{\!\!}^{(I)}}{\frac {DQ_{\mathrm {rev} }}{T}}+{\int \limits _{2}\limits ^{1}}_{{\!\!}^{(II)}}{\frac {DQ_{\mathrm {rev} }}{T}}=\oint dS_{\mathrm {rev} }=0.$

This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2.

Many, in fact most, thermodynamic processes are spontaneous and irreversible. A well-known spontaneous process is the flow of heat from a hot to a cold body. The opposite process—the transport of heat from a cold to a hot body—needs work (by the Clausius principle), the process is not spontaneous and accordingly not the reverse of the spontaneous flow of heat from hot to cold bodies. Another example of an irreversible process is Count Rumford's seminal cannon boring experiment where work is converted by friction into heat. It is impossible to revert this process, which is intuitively clear, but also contradicts the Kelvin principle, the impossibility of obtaining work from a single source of heat. The Joule-Thomson effect is yet another example of an irreversible process.

References

C. S. Helrich, Modern Thermodynamics with Statistical Mechanics, Springer (2009). Google books