User:Boris Tsirelson/Sandbox1

In Newtonian mechanics, coordinates of moving bodies are functions of time. For example, the classical equation for a falling body; its height h at a time t is

$h=f(t)=h_{0}-0.5gt^{2}$

(here h₀ is the initial height, and g is the acceleration due to gravity). Infinitely many corresponding values of t and h are embraced by a single function f.

PD Image
Vibrating string: a function changes in time

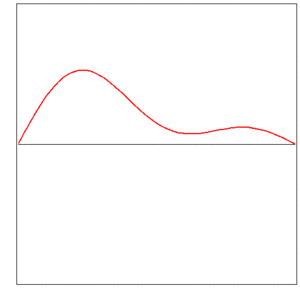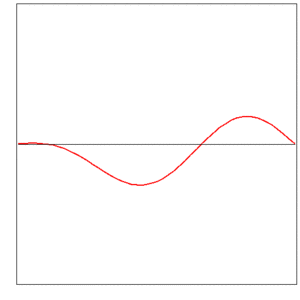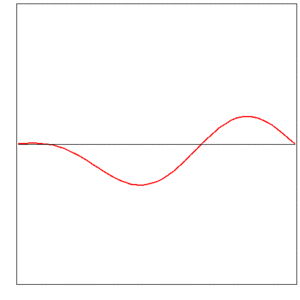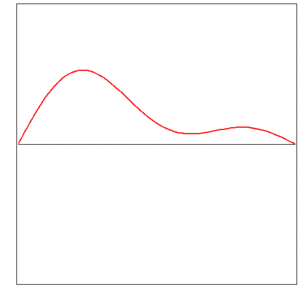
The instantaneous shape of a vibrating string is described by a function (the displacement y as a function of the coordinate x), and this function changes in time:

$y=f_{t}(x).$

Infinitely many functions f_t are embraced by a single function f of two variables,

$y=f(x,t).$

After some speculations by Galileo and mathematical interpretation by Brook Taylor (1715), the mathematical theory of vibrating string was started by Jean d'Alembert (communicated in 1746, published in 1749). His approach is equivalent to a partial differential equation written out by Leonhard Euler in 1755,

${\frac {\partial ^{2}f(x,t)}{\partial x^{2}}}={\frac {\partial ^{2}f(x,t)}{\partial t^{2}}},$

now well-known as the one-dimensional wave equation.