Rectangle: Difference between revisions
imported>Anthony Argyriou (create) |
mNo edit summary |
||
| Line 9: | Line 9: | ||
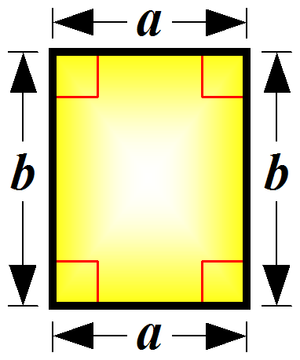
The perimeter of a rectangle is equal to 2 times the length of the sum of two adjacent sides. The area of a rectangle is equal to the product of two adjacent sides. The diagonal of a rectangle is <math>\scriptstyle \sqrt{a^2+b^2}</math> where ''a'' and ''b'' are the lengths of two adjacent sides, as can be easily shown from the [[Pythagorean theorem]]. | The perimeter of a rectangle is equal to 2 times the length of the sum of two adjacent sides. The area of a rectangle is equal to the product of two adjacent sides. The diagonal of a rectangle is <math>\scriptstyle \sqrt{a^2+b^2}</math> where ''a'' and ''b'' are the lengths of two adjacent sides, as can be easily shown from the [[Pythagorean theorem]]. | ||
A rectangle can [[tile (mathematics)|tile]] a plane with no voids. | A rectangle can [[tile (mathematics)|tile]] a plane with no voids.[[Category:Suggestion Bot Tag]] | ||
Latest revision as of 11:01, 10 October 2024
A rectangle is a polygon of four sides with the four vertex angles equal. All four angles are 90 degrees. A rectangle is a special case of a parallelogram where all four angles are equal. A square is a special case of rectangle, where all four sides are of equal length.
Properties
As with all quadrilaterals, the sum of the interior angles of a rectangle is 360 degrees; since the four angles are equal, each interior angle is 90 degrees.
The perimeter of a rectangle is equal to 2 times the length of the sum of two adjacent sides. The area of a rectangle is equal to the product of two adjacent sides. The diagonal of a rectangle is where a and b are the lengths of two adjacent sides, as can be easily shown from the Pythagorean theorem.
A rectangle can tile a plane with no voids.