Reflection (geometry)

In analytic geometry, a reflection is a linear operation σ on a vector space with σ² = 1, i.e., σ is an involution. Reflecting twice an arbitrary vector brings back the original vector :

$\sigma ({\vec {\mathbf {r} }}\,)={\vec {\mathbf {r} }}\,'\quad {\hbox{and}}\quad \sigma ({\vec {\mathbf {r} }}\,'\,)={\vec {\mathbf {r} }}.$

PD Image
The vector $\scriptstyle {\vec {\mathbf {r} }}$ goes to $\scriptstyle {\vec {\mathbf {r} }}'$ under reflection in a plane. The unit vector $\scriptstyle {\hat {\mathbf {n} }}$ is normal to mirror plane.

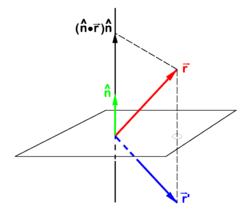
Reflection in a plane

If ${\hat {\mathbf {n} }}$ is a unit vector normal (perpendicular) to a plane—the mirror plane—then $({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$ is the projection of ${\vec {\mathbf {r} }}$ on this unit vector. From the figure it is evident that

${\vec {\mathbf {r} }}-{\vec {\mathbf {r} }}\,'=2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }})\,{\hat {\mathbf {n} }}\;\Longrightarrow \;{\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$

If a non-unit normal ${\vec {\mathbf {n} }}$ is used then substitution of

${\hat {\mathbf {n} }}={\frac {\vec {\mathbf {n} }}{|{\vec {\mathbf {n} }}|}}\equiv {\frac {\vec {\mathbf {n} }}{n}}$

gives the mirror image,

${\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2{\frac {({\vec {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\vec {\mathbf {n} }}}{n^{2}}}$

This relation can be immediately generalized to m-dimensional inner product spaces. Let the space V_m allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,

$V_{m}=V_{1}\oplus V_{m-1}$

and let v be an element of the one-dimensional space V₁ then the involution

$r\mapsto r-2v{\frac {(v,r)}{(v,v)}}$

is a reflection of r in the hyperplane V_m−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.