Reflection (geometry): Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 29: | Line 29: | ||
is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | ||
==Two consecutive reflections== | ==Two consecutive reflections== | ||
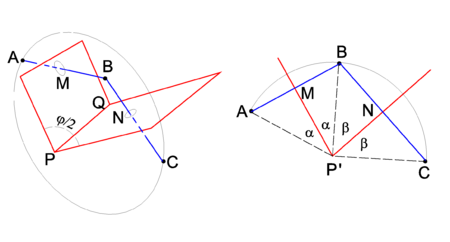
{{Image|Two reflections.png|right| | {{Image|Two reflections.png|right|450px|Fig. 2. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′}} | ||
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. | Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. | ||
The | The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2. | ||
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an [[orthogonal matrix]] with [[determinant]] −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det('''AB''') = det('''A''')det('''B'''), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation. | From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an [[orthogonal matrix]] with [[determinant]] −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det('''AB''') = det('''A''')det('''B'''), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation. | ||
Revision as of 10:04, 18 July 2009
In analytic geometry, a reflection is a linear operation σ on a vector space with σ2 = 1, i.e., σ is an involution. Reflecting twice an arbitrary vector brings back the original vector :
Reflection in a plane
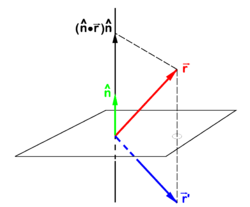
If is a unit vector normal (perpendicular) to a plane—the mirror plane—then is the projection of on this unit vector. From the figure it is evident that
If a non-unit normal is used then substitution of
gives the mirror image,
This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,
and let v be an element of the one-dimensional space V1 then the involution
is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.
Two consecutive reflections
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an orthogonal matrix with determinant −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det(AB) = det(A)det(B), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation.