Ellipse

PD Image
Fig. 1. Ellipse (black closed curve). The sum of the lengths of the two red line segments (ending in P₁) is equal to the sum of the lengths of the two blue line segments (ending in P₂).

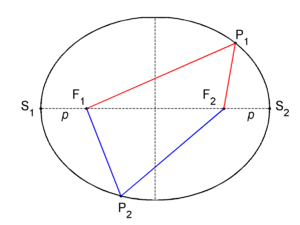
In mathematics, an ellipse is a planar locus of points characterized by having a constant sum of distances to two given fixed points in the plane. In figure 1 two fixed points F₁ and F₂ are shown, these are the foci of the ellipse. An arbitrary point P₁ on the ellipse has distance F₁P₁ to F₁ and distance F₂P₁ to F₂. Let d be the sum of distances of P₁ to the foci,

$d\equiv \mathrm {F} _{1}\mathrm {P} _{1}+\mathrm {F} _{2}\mathrm {P} _{1},$

then all points of the ellipse have the constant sum of distances d. Thus, another arbitrary point P₂ on the ellipse has distance F₁P₂ to F₁ and distance F₂P₂ to F₂. By definition the sum of distances of P₂ to the foci is equal to d,

$\mathrm {F} _{1}\mathrm {P} _{2}+\mathrm {F} _{2}\mathrm {P} _{2}=d.\,$

The horizontal line segment S₁–S₂ in figure 1, going through the foci, is known as the major axis of the ellipse. Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway the foci perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and minor axes are distinguished by a ≥ b. When a = b the ellipse is a circle—a special case of an ellipse. Clearly both axes are symmetry axes, reflection in either of them transforms the ellipse into itself. Basically, this a consequence of the fact that a reflection conserves (sums of) distances. The intersection of the axes is the center of the ellipse.

The two foci and the points S₁ and S₂ are connected by reflection in the minor axis. Hence the distance S₂F₂ ≡ p is by symmetry equal to the distance S₁F₁. The distance of S₂ to F₁ is equal to 2a − p. By the definition of the ellipse the sum is equal to d, hence

$d=2a-p+p=2a.\;$

The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis.

Conic section

PD Image
Fig. 2. Upper shaded (green) section: ellipse; lower shaded (red) section: circle.

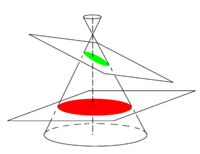
In the work of the Greek mathematician Apollonius (c. 262–190 BC) the ellipse arose as the intersection of a plane with a cone. Apollonius gave the ellipse its name, though the term ἐλλειψις (elleipsis, meaning "falling short") was used earlier by Euclid (c. 300 BC) in the construction of parallelograms with areas that "fell short". Apollonius applied the word to the conic section that at present we call ellipse. See Ref. for the—in modern eyes—complicated reasoning by which Apollonius tied the shape of certain conic sections to Euclid's concept of deficient areas.

In figure 2 a cone with a circular base is shown. It has a vertical symmetry axis, an axis of revolution. A cone can be generated by revolving around the axis a line that intersects the symmetry axis under an angle. A horizontal intersecting plane (plane perpendicular to the symmetry axis of the cone) gives a circle (a special ellipse), that is, the intersection of a horizontal plane with the cone is a circle. Planes that make an angle less than, or equal to, 90^° (but more than half the top angle of the cone) with the axis have an ellipse as intersection.

Eccentricity

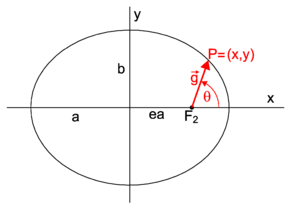
The eccentricity e of an ellipse (usually denoted by e or ε) is the ratio of the distance OF₂ (cf. figure 3) to half the length a of the major axis, that is, e ≡ OF₂ / a. Let ${\vec {a}}$ be a vector of length a along the x-axis, then

$e{\vec {a}}\equiv {\overrightarrow {\mathrm {OF} }}_{2}.$

The following two vectors have common endpoint at P, see figure 3,

${\vec {r}}={\overrightarrow {\mathrm {OP} }}={\begin{pmatrix}x\\y\end{pmatrix}}\quad {\hbox{and}}\quad {\vec {g}}\equiv {\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=-e{\vec {a}}+{\vec {r}}.$

Move P now to the positive y-axis; its new position vector is:

${\vec {r}}={\begin{pmatrix}0\\b\end{pmatrix}}.$

By symmetry, the distance of the moved P to either focus is equal to half the length of the major axis (a) and equal to the length of the new vector ${\vec {g}}$ (with endpoint on the y-axis). For the following two inner products (indicated by a centered dot) we find,

${\vec {r}}\cdot (e{\vec {a}})=0\quad {\hbox{and}}\quad {\vec {r}}\cdot {\vec {r}}=b^{2}.$

PD Image
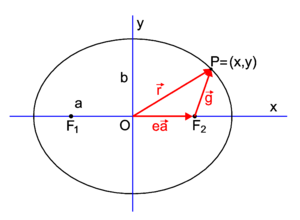
Fig. 3. An ellipse situated such that the major and minor axis are along Cartesian axes. The center of the ellipse coincides with the origin O.

Hence, (in fact by the Pythagoras theorem applicable for P on the y-axis),

$|{\vec {g}}\;|^{2}=a^{2}=({\vec {r}}-e{\vec {a}}\;)\cdot ({\vec {r}}-e{\vec {a}}\;)=b^{2}+e^{2}a^{2},$

so that the eccentricity is given by

$e={\sqrt {\frac {a^{2}-b^{2}}{a^{2}}}}\quad {\hbox{with}}\quad 0\leq e\leq 1.$

Algebraic form

Consider an ellipse that is located with respect to a Cartesian frame as in figure 3 (major axis on x-axis, minor axis on y-axis). For a point P=(x,y) of the ellipse it holds that

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Note that this equation is reminiscent of the equation for a unit circle. An ellipse may be seen as a unit circle in which the x and the y coordinates are scaled independently, by 1/a and 1/b, respectively.

Proof

Introduce the vectors

${\begin{aligned}{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{1}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&\;e{\vec {a}}+{\vec {r}}\\{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}={\overrightarrow {\mathrm {F} _{2}\mathrm {O} }}+{\overrightarrow {\mathrm {O} \mathrm {P} }}=&-e{\vec {a}}+{\vec {r}}={\vec {g}}\\\end{aligned}}$

By definition of ellipse, the sum of the lengths is 2a

$|{\vec {r}}+e{\vec {a}}|+|{\vec {r}}-e{\vec {a}}|=2a\qquad \qquad \qquad \qquad (1)$

Multiply Eq. (1) by

$|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|$

and work out the left-hand side:

$|{\vec {r}}+e{\vec {a}}|^{2}-|{\vec {r}}-e{\vec {a}}|^{2}=4e{\vec {r}}\cdot {\vec {a}}$

Hence

$4e{\vec {r}}\cdot {\vec {a}}=2a(|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|)$

Use

${\frac {{\vec {r}}\cdot {\vec {a}}}{a}}=x$

and one obtains

$|{\vec {r}}+e{\vec {a}}|-|{\vec {r}}-e{\vec {a}}|=2ex\qquad \qquad \qquad \qquad (2)$

Add and subtract Eqs (1) and (2) and we find expressions for the distance of P to the foci,

${\begin{aligned}|{\overrightarrow {\mathrm {F} _{1}\mathrm {P} }}|&=|{\vec {r}}+e{\vec {a}}|&=a+ex&\\|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|&=|{\vec {r}}-e{\vec {a}}|&=a-ex&\qquad \qquad \qquad \quad (3)\\\end{aligned}}$

Square both equations

${\begin{aligned}r^{2}+e^{2}a^{2}+2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}+2eax\\r^{2}+e^{2}a^{2}-2e{\vec {r}}\cdot {\vec {a}}&=a^{2}+e^{2}x^{2}-2eax\\\end{aligned}}$

Adding, using the earlier derived value for e², and reworking gives

$r^{2}+e^{2}a^{2}=a^{2}+e^{2}x^{2}\Longrightarrow r^{2}+a^{2}-b^{2}=a^{2}+{\frac {x^{2}}{a^{2}}}(a^{2}-b^{2})\Longrightarrow x^{2}+y^{2}=b^{2}+x^{2}-x^{2}{\frac {b^{2}}{a^{2}}}\Longrightarrow y^{2}=b^{2}-x^{2}{\frac {b^{2}}{a^{2}}}$

Division by b² gives finally

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.$

Polar representation relative to focus

PD Image
Fig. 4. Polar representation

The length g of the vector (cf. figure 4)

${\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}\equiv {\vec {g}}=(ea+g\cos \theta ,\;g\sin \theta )$

is given by the polar equation

$g={\frac {\ell }{1+e\cos \theta }}\quad {\hbox{with}}\quad \ell \equiv {\frac {b^{2}}{a}},$

where 2ℓ is known as the latus rectum (lit. right side) of the ellipse; it is equal to 2g for θ = 90^° (twice the length of the vector ${\vec {g}}$ when it makes a right angle with the major axis).

Proof

Earlier [Eq. (3)] it was derived for the distance from the right focus F₂ to P that

$|{\overrightarrow {\mathrm {F} _{2}\mathrm {P} }}|\equiv |{\vec {g}}|\equiv g=a-ex.$

Elimination of x from

$x=ea+g\cos \theta =ea+(a-ex)\cos \theta \,$

gives

$x={\frac {ea+a\cos \theta }{1+e\cos \theta }},$

so that

$g=a-ex=a-{\frac {e^{2}a+ea\cos \theta }{1+e\cos \theta }}={\frac {a(1-e^{2})}{1+e\cos \theta }}.$

Substitute

$a(1-e^{2})=a(1-{\frac {a^{2}-b^{2}}{a^{2}}})={\frac {b^{2}}{a}}\equiv \ell$

and the polar equation for the ellipse follows.