Semiconductor: Difference between revisions
imported>John R. Brews (→Density of states: section and figure on impurities) |
imported>John R. Brews (remove some redundancy) |
||
| Line 13: | Line 13: | ||
==Dopant impurities== | ==Dopant impurities== | ||
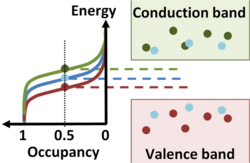
{{Image|Fermi levels.PNG|right|250px|Occupancy comparison between n-type, intrinsic and p-type semiconductors}} | {{Image|Fermi levels.PNG|right|250px|Occupancy comparison between n-type, intrinsic and p-type semiconductors}} | ||
The number of electrons and holes present in a semiconductor can be adjusted by introducing impurities into the semiconductor that alter the balance, allowing the hole and electrons densities to differ. The impurities may either increase the number of electrons in the conduction band (called ''donor impurities''), or increase the number of holes in the valence band (called ''acceptor impurities''). Semiconductors in which electrons dominate are called ''n-type'', those where holes dominate conduction are called ''p-type'', and those that do not have impurities and exhibit equal hole and electron concentrations are called ''intrinsic''. | The number of electrons and holes present in a semiconductor can be adjusted by introducing impurities into the semiconductor that alter the balance, allowing the hole and electrons densities to differ. The added impurities that control the occupancy of energy levels are called ''dopants''. The impurities may either increase the number of electrons in the conduction band (called ''donor impurities''), or increase the number of holes in the valence band (called ''acceptor impurities''). Semiconductors in which electrons dominate are called ''n-type'', those where holes dominate conduction are called ''p-type'', and those that do not have impurities and exhibit equal hole and electron concentrations are called ''intrinsic''. | ||
The figure shows the [[Fermi function]] on the left at a non-zero temperature for the intrinsic case (equal numbers of holes and electrons), the ''p''-type case with holes, and the ''n''-type case with electrons. The horizontal dashed lines indicate how the half-occupancy line is shifted by impurities. | The figure shows the [[Fermi function]] on the left at a non-zero temperature for the intrinsic case (equal numbers of holes and electrons), the ''p''-type case with holes, and the ''n''-type case with electrons. The horizontal dashed lines indicate how the half-occupancy line is shifted by impurities. Impurities that act as ''donors'', move the Fermi half-occupancy level closer to the conduction band edge, while impurities called ''acceptors'' move the Fermi half-occupancy level closer to the valence band. | ||
In the case where the impurity substitutes for a host atom in the semiconductor lattice, the explanation as to why impurities behave as donors or as acceptors is based upon the valence of the substituting atom. The idea is that the substitute must try to emulate a host atom in the lattice by approximating its electron distribution. Thus, acceptor impurities must "borrow" an electron for this masquerade, becoming negatively charged, while donor impurities must yield an electron and become positively charged. | In the case where the impurity substitutes for a host atom in the semiconductor lattice, the explanation as to why impurities behave as donors or as acceptors is based upon the valence of the substituting atom. The idea is that the substitute must try to emulate a host atom in the lattice by approximating its electron distribution. Thus, acceptor impurities must "borrow" an electron for this masquerade, becoming negatively charged, while donor impurities must yield an electron and become positively charged. | ||
| Line 38: | Line 38: | ||
The conduction band edge also is lowered, increasing electron occupancy of these states, but at low voltages this increase is not significant. At larger applied voltages, however, as in the bottom panel, the conduction band edge is lowered sufficiently to cause significant population of these levels in a narrow surface layer, called an ''inversion'' layer because the electrons are opposite in polarity to the holes originally populating the semiconductor. This onset of electron charge in the inversion layer becomes very significant at an applied ''threshold'' voltage, and once the applied voltage exceeds this value charge neutrality is achieved almost entirely by addition of electrons to the inversion layer rather than by an increase in acceptor ion charge by expansion of the depletion layer. Further field penetration into the semiconductor is arrested at this point, as the electron density increases exponentially with band-bending beyond the threshold voltage, effectively ''pinning'' the depletion layer depth at its value at threshold voltage. | The conduction band edge also is lowered, increasing electron occupancy of these states, but at low voltages this increase is not significant. At larger applied voltages, however, as in the bottom panel, the conduction band edge is lowered sufficiently to cause significant population of these levels in a narrow surface layer, called an ''inversion'' layer because the electrons are opposite in polarity to the holes originally populating the semiconductor. This onset of electron charge in the inversion layer becomes very significant at an applied ''threshold'' voltage, and once the applied voltage exceeds this value charge neutrality is achieved almost entirely by addition of electrons to the inversion layer rather than by an increase in acceptor ion charge by expansion of the depletion layer. Further field penetration into the semiconductor is arrested at this point, as the electron density increases exponentially with band-bending beyond the threshold voltage, effectively ''pinning'' the depletion layer depth at its value at threshold voltage. | ||
Revision as of 15:34, 7 January 2011
A semiconductor is a substance with electrical conductivity intermediate between metals and insulators. Most commonly these materials are solids.
Density of states
In liquid and solid materials where atoms are in close proximity to one another, the energy levels available to electrons fall into bands separated by energy gaps. The density of energy levels per unit energy as a function of energy might look as in the figure. This density of states relate to the semiconducting behavior of this material as follows:
- Bands of allowed energy are separated by an energy gap. Those above the gap are called conduction band energy levels, and those below are valence band energy levels.
- At low temperatures, electrons occupy all the energy levels below the gap, and none above the gap.
- The energy gap is small enough that at normal temperatures some electrons can acquire thermal energy sufficient to occupy a few conduction band energy levels above the gap, leaving vacant levels (holes) in the valence band energy levels below the gap.
- The conduction band energy levels, and possibly the higher-energy hole energy levels too, correspond to states spatially extended through large regions of the material and are not localized. That spatial extension means that conduction-band electrons (and possibly valence-band holes too) can travel easily (conduct) by moving between adjacent levels in response to an applied field.
Dopant impurities
The number of electrons and holes present in a semiconductor can be adjusted by introducing impurities into the semiconductor that alter the balance, allowing the hole and electrons densities to differ. The added impurities that control the occupancy of energy levels are called dopants. The impurities may either increase the number of electrons in the conduction band (called donor impurities), or increase the number of holes in the valence band (called acceptor impurities). Semiconductors in which electrons dominate are called n-type, those where holes dominate conduction are called p-type, and those that do not have impurities and exhibit equal hole and electron concentrations are called intrinsic.
The figure shows the Fermi function on the left at a non-zero temperature for the intrinsic case (equal numbers of holes and electrons), the p-type case with holes, and the n-type case with electrons. The horizontal dashed lines indicate how the half-occupancy line is shifted by impurities. Impurities that act as donors, move the Fermi half-occupancy level closer to the conduction band edge, while impurities called acceptors move the Fermi half-occupancy level closer to the valence band.
In the case where the impurity substitutes for a host atom in the semiconductor lattice, the explanation as to why impurities behave as donors or as acceptors is based upon the valence of the substituting atom. The idea is that the substitute must try to emulate a host atom in the lattice by approximating its electron distribution. Thus, acceptor impurities must "borrow" an electron for this masquerade, becoming negatively charged, while donor impurities must yield an electron and become positively charged.
For example, if a column III impurity like B, Al, Ga or In, is added to silicon, these trivalent atoms grab an electron because they have only three electrons to bond with neighboring atoms, while a silicon atom has four. Similarly, addition of column V atoms, like P, As, Sb, to silicon, which have five electrons in their outer orbitals require only four for bonding, and donate the fifth electron.
This picture is complicated in a compound semiconductor like GaAs (a III-V semiconductor) that has more than one type of atom in the lattice. So, for example, a column VI atom like S, Se and Te can act as a donor if it occupies the site of the column V As host atom, and column II atoms like Be, Mg and Zn can act as acceptors if they replace Ga host atoms. On the other hand, a column IV atom like Si can act as either a donor or an acceptor depending upon whether Si replaces Ga or As.
Where an electron is borrowed, the occupancy of the valence band must be decreased. That means the Fermi occupancy level moves lower, closer to the valence band edge. Conversely, for donors, the occupancy of the conduction band must increase, so the Fermi occupancy level moves closer to the conduction band edge.
Electric field penetration
Top panel: Applied voltage bends bands, depleting holes from surface (left). The charge inducing the bending is balanced by a layer of negative acceptor-ion charge, as shown on the upper right. Bottom panel: Larger applied voltage further depletes holes but conduction band becomes low enough in energy to populate an inversion layer.
In a metal the electron density that responds to applied fields is so large that an external electric field can penetrate only a very short distance into the material. However, in a semiconductor the lower density of electrons (and possibly holes) that can respond to an applied field is sufficiently small that the field can penetrate quite far into the material. A consequence is that the energy levels available to electrons are altered by the applied field to considerable depths from the surface, and that in turn changes the occupancy of the energy levels in the surface region. A typical treatment of such effects is based upon a band bending diagram showing the positions in energy of the band edges as a function of depth into the material.
An example band-bending diagram is shown in the figure for a two-layer structure consisting of an insulator as left-hand layer and a semiconductor as right-hand layer. An example of such a structure is the MOS capacitor, a two terminal structure made up of a metal gate contact, a semiconductor body (such as silicon) with a body contact, and an intervening insulating layer (such as silicon dioxide, hence the designation O). The left panels show the lowest energy level of the conduction band and the highest energy level of the valence band. These levels are "bent" by the application of a positive voltage V. By convention, the energy of electrons is shown, so a positive voltage penetrating the surface lowers the conduction edge. A dashed line depicts the occupancy situation: below this Fermi level the states are occupied and above it they are empty, assuming zero temperature. At operating temperatures, however, some electrons populate the conduction band, and some vacancies (holes) populate the valence band.
The example in the figure shows the Fermi occupancy level in the bulk material beyond the range of the applied field as lying close to the valence band edge. This position for the occupancy level is arranged by introducing impurities into the semiconductor. In this case the impurities are so-called acceptors which soak up electrons from the valence band becoming negatively charged, immobile ions embedded in the semiconductor material. The removed electrons are drawn from the valence band levels, leaving vacancies or holes in the valence band. Charge neutrality prevails because the negative acceptor ion has created a positive deficiency in the host material: a hole is the absence of an electron, it behaves like a positive charge. When no field is present, neutrality is achieved because the negative acceptor ions exactly balance the positive holes.
Next the band bending is described. A positive charge is placed on the left face of the insulator (for example using a metal "gate" electrode). In the insulator there are no charges so the electric field is constant, leading to a linear change of voltage in this material. As a result, the insulator conduction and valence bands are therefore straight lines in the figure, separated by the large insulator energy gap.
In the semiconductor at the smaller voltage shown in the top panel, the positive charge placed on the left face of the insulator lowers the energy of the valence band edge. Consequently, these states are fully occupied out to a so-called depletion depth where the bulk occupancy reestablishes itself because the field cannot penetrate further. Because the valence band levels near the surface are fully occupied due to the lowering of these levels, only the immobile negative acceptor-ion charges are present near the surface, which becomes a region without holes (the depletion layer). Thus, field penetration is arrested when the exposed negative acceptor ion charge balances the positive charge placed on the insulator surface: the depletion layer adjusts its depth enough to make the net negative acceptor ion charge balance the positive charge on the gate.
The conduction band edge also is lowered, increasing electron occupancy of these states, but at low voltages this increase is not significant. At larger applied voltages, however, as in the bottom panel, the conduction band edge is lowered sufficiently to cause significant population of these levels in a narrow surface layer, called an inversion layer because the electrons are opposite in polarity to the holes originally populating the semiconductor. This onset of electron charge in the inversion layer becomes very significant at an applied threshold voltage, and once the applied voltage exceeds this value charge neutrality is achieved almost entirely by addition of electrons to the inversion layer rather than by an increase in acceptor ion charge by expansion of the depletion layer. Further field penetration into the semiconductor is arrested at this point, as the electron density increases exponentially with band-bending beyond the threshold voltage, effectively pinning the depletion layer depth at its value at threshold voltage.