Plane (geometry): Difference between revisions
imported>Miguel Adérito Trigueira (→Rectilinear figure: +Rectilinear figures include triangles and polygons.) |
imported>Thomas Wright Sulcer (adding diagram) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
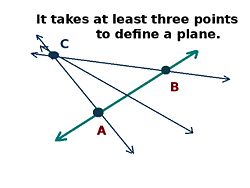
[[Image:A plain plane.jpg|thumb|250px|alt=Diagram of a plane with three points.|An infinite number of lines can be drawn from point C to the line AB, and this would form a plane.]] | |||
A '''plane''' is a [[surface]] such that any straight [[line]] linking any two [[point]]s on the surface is part of the surface. | A '''plane''' is a [[surface]] such that any straight [[line]] linking any two [[point]]s on the surface is part of the surface. | ||
Revision as of 17:07, 17 March 2010
Please create the "Talk page". Just click this Talk page link and save the page.
A plane is a surface such that any straight line linking any two points on the surface is part of the surface. A plane is made up of an infinite number of straight lines. At its simplest, a plane can be defined by a triangle whose vertices cannot be collinear.
In Euclidean geometry: A plane is a surface on which a line perpendicular to a line which lies on that surface also falls entirely on the surface. It can be described by three points which do not lie on the same line. A line is said to lie on a surface if its points fall on the surface. Surfaces can be parallel.
To distinguish between a plane and a surface think of a surface as a piece of paper (with no thickness) that could be twisted, or rolled, or crumpled up. A plane would be like that sheet of paper lying perfectly flat on a table.
A surface is usually designated by the names of the points which fall on it. Thus the surface has on it point A, point B, and point C is called surface ABC.
Plane figure
A plain figure is a combination of points and/or lines that fall on the same plane.
Rectilinear figure
A rectilinear figure is a plane figure consisting of straight lines only. Rectilinear figures include triangles and polygons.