Pythagorean theorem: Difference between revisions
imported>Yitzchak Novick (completed proof) |
imported>Jitse Niesen (formatting and some minor rewriting of the proof) |
||
| Line 10: | Line 10: | ||
The Pythagorean theorem is commonly known by its algebraic notation: | The Pythagorean theorem is commonly known by its algebraic notation: | ||
:<math> a^2 + b^2 = c^2 \, </math> | |||
where a and b | where ''a'' and ''b'' denote the lengths of the two legs of the right triangle and ''c'' is the length of the hypotenuse. | ||
===Proof of the Pythagorean | ===Proof of the Pythagorean theorem=== | ||
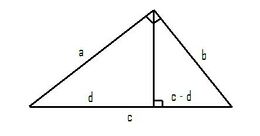
Take a right triangle with legs of length a and b and hypotenuse of length c. Draw a line from the right angle perpendicular to the hypotenuse | Take a right triangle with legs of length ''a'' and ''b'' and hypotenuse of length ''c''. Draw a line from the right angle perpendicular to the hypotenuse as pictured. This line divides the hypotenuse into two segments. Suppose one of them have length ''d'', then the other one has length ''c'' – ''d''. | ||
[[Image:pythagProof.jpg| | [[Image:pythagProof.jpg|thumb|260px|A right triangle with the line from the right angle perpendicular to the hypothenuse.]] | ||
This line divides the triangle into two smaller triangles, both of which are [[similar triangles|similar]] to the original triangle. (This is evident by the fact that both of these new triangles are right triangles and share a second angle with the original triangle.) Because these triangles are similar to the original triangle, the following proportions hold: | This line divides the triangle into two smaller triangles, both of which are [[similar triangles|similar]] to the original triangle. (This is evident by the fact that both of these new triangles are right triangles and share a second angle with the original triangle.) Because these triangles are similar to the original triangle, the following proportions hold: | ||
:<math> \frac{a}{c} = \frac{d}{a} \quad\text{and}\quad \frac{b}{c} = \frac{c-d}{b}. </math> | |||
[[cross multiplication| | [[cross multiplication|Cross multiplying]] both equations gives: | ||
:<math> a^2 = cd \, </math> | |||
and | and | ||
:<math> b^2 = c(c-d) \quad\text{or}\quad b^2 = c^2 - cd. </math> | |||
or | |||
b | |||
Adding both equation gives | |||
:<math> a^2 + b^2 = c^2 \, </math> | |||
which completes the proof. | |||
Revision as of 03:48, 4 August 2008
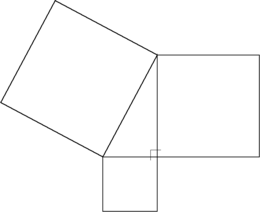
In Euclidean geometry, the Pythagorean theorem states that:
- The sum of the areas of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle.
The Pythagorean theorem is commonly known by its algebraic notation:
where a and b denote the lengths of the two legs of the right triangle and c is the length of the hypotenuse.
Proof of the Pythagorean theorem
Take a right triangle with legs of length a and b and hypotenuse of length c. Draw a line from the right angle perpendicular to the hypotenuse as pictured. This line divides the hypotenuse into two segments. Suppose one of them have length d, then the other one has length c – d.
This line divides the triangle into two smaller triangles, both of which are similar to the original triangle. (This is evident by the fact that both of these new triangles are right triangles and share a second angle with the original triangle.) Because these triangles are similar to the original triangle, the following proportions hold:
Cross multiplying both equations gives:
and
Adding both equation gives
which completes the proof.