Law of sines: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 7: | Line 7: | ||
\frac{\sin\alpha}{a} = \frac{\sin\beta}{b}= \frac{\sin{\gamma}}{c} = \frac{1}{d}, | \frac{\sin\alpha}{a} = \frac{\sin\beta}{b}= \frac{\sin{\gamma}}{c} = \frac{1}{d}, | ||
</math> | </math> | ||
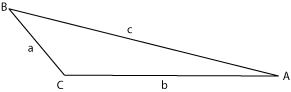
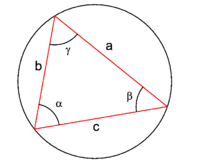
where ''d'' is the diameter of the circle circumscribing the triangle | where ''d'' is the diameter of the circle circumscribing the triangle. The angles and the lengths of the sides are defined in Fig. 1 for an obtuse-angled triangle and in Fig. 2 for an acute-angled triangle. | ||
From the law of sines follows that the ratio of the sines of the angles of a triangle is equal to the ratio of the lengths of the opposite sides. | |||
[[Image:Sine rule.png|right|thumb|300px|Fig. 2. '''Sine rule:''' sinα:sinβ:sinγ=a:b:c]] | [[Image:Sine rule.png|right|thumb|300px|Fig. 2. '''Sine rule:''' sinα:sinβ:sinγ=a:b:c]] | ||
The rule is useful to determine unknown angles and sides of a triangle | |||
* One side, the opposite angle, and one adjacent angle. | The rule is useful to determine unknown angles and sides of a triangle in any of the following three cases: | ||
* One side and two adjacent angles | * One side, the opposite angle, and one adjacent angle are given. | ||
* Two sides and an angle not included by the sides. | * One side and two adjacent angles are given. | ||
* Two sides and an angle not included by the sides are given. | |||
The rule | The rule | ||
:<math> | :<math> | ||
| Line 22: | Line 25: | ||
==Proof== | ==Proof== | ||
The easiest proof is purely geometric, not algebraic. | The easiest proof is purely geometric, not algebraic. | ||
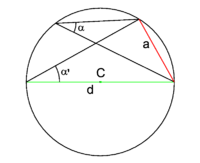
[[Image:Proof sine rule.png|left|thumb|200px|Fig. 3. The angles α and α' share the chord ''a''. The center of the circle is at ''C'' and its diameter is ''d''.]] | [[Image:Proof sine rule.png|left|thumb|200px|Fig. 3. The angles α and α' share the chord ''a''. The center of the circle is at ''C'' and its diameter is ''d''.]] | ||
In Fig. 3 the arbitrary angle α satisfies | '''Lemma''': In Fig. 3 the arbitrary angle α satisfies | ||
<math> \sin\alpha = \frac{a}{d}, </math> | |||
\sin\alpha = \frac{a}{d}, | where ''d'' is the diameter of the circle and ''a'' is the chord opposite α. To prove this we consider the angle α' that has the diameter of the circle as one of its sides, and the other side perpendicular to the chord ''a'', see Fig. 3. The two angles, α and α' share a segment of the circle (have the chord ''a'' in common). The angle α', has the diameter of the circle ''d'' as one of its sides and has as opposite angle a right angle. Hence sin(α') = ''a''/''d'', the length of chord ''a'' divided by the diameter ''d''. A well-known theorem of plane geometry states that α = α' and it follows that the angle α has the same sine as α'. | ||
</math> | |||
where ''d'' is the diameter of the circle and ''a'' is the chord opposite α. To prove this we consider the angle α' that has the diameter of the circle as one of its sides, see Fig. 3. The two angles, α and α' share a segment of the circle (have the chord ''a'' in common). The angle α', | |||
[[Image:Proof sine rule2.png|right|thumb|200px|Fig. 4]] | [[Image:Proof sine rule2.png|right|thumb|200px|Fig. 4]] | ||
| Line 34: | Line 35: | ||
===Proof of sine rule=== | ===Proof of sine rule=== | ||
From the lemma follows that the angles in Fig. 4 are | From the lemma follows that the angles in Fig. 4 are | ||
:<math> | :<math> | ||
\sin\alpha = \frac{a}{d}, \quad\sin\beta = \frac{b}{d},\quad\sin\gamma = \frac{c}{d}, | \sin\alpha = \frac{a}{d}, \quad\sin\beta = \frac{b}{d},\quad\sin\gamma = \frac{c}{d}, | ||
</math> | </math> | ||
Revision as of 05:18, 21 October 2008
In trigonometry, the law of sines (also known as sine rule) relates in a triangle the sines of the three angles and the lengths of their opposite sides,
where d is the diameter of the circle circumscribing the triangle. The angles and the lengths of the sides are defined in Fig. 1 for an obtuse-angled triangle and in Fig. 2 for an acute-angled triangle.
From the law of sines follows that the ratio of the sines of the angles of a triangle is equal to the ratio of the lengths of the opposite sides.
The rule is useful to determine unknown angles and sides of a triangle in any of the following three cases:
- One side, the opposite angle, and one adjacent angle are given.
- One side and two adjacent angles are given.
- Two sides and an angle not included by the sides are given.
The rule
may be useful in such a determination.
The use of the law of sines is complementary to the use of the law of cosines.
Proof
The easiest proof is purely geometric, not algebraic.
Lemma: In Fig. 3 the arbitrary angle α satisfies where d is the diameter of the circle and a is the chord opposite α. To prove this we consider the angle α' that has the diameter of the circle as one of its sides, and the other side perpendicular to the chord a, see Fig. 3. The two angles, α and α' share a segment of the circle (have the chord a in common). The angle α', has the diameter of the circle d as one of its sides and has as opposite angle a right angle. Hence sin(α') = a/d, the length of chord a divided by the diameter d. A well-known theorem of plane geometry states that α = α' and it follows that the angle α has the same sine as α'.
Proof of sine rule
From the lemma follows that the angles in Fig. 4 are
where d is the diameter of the circle. This proves the sine rule.