Russell-Saunders coupling

In atomic spectroscopy, Russell–Saunders coupling, also known as L–S coupling, specifies a coupling scheme of electronic spin- and orbital-angular momenta.

In Russell-Saunders coupling—called after H. N. Russell and F. A. Saunders—the orbital angular momentum eigenstates of the electrons are coupled to eigenstates with quantum number L of the total angular momentum operator squared L². Separately the one-electron spin functions are coupled to eigenstates with quantum number S of total S². Sometimes there is further coupling to J ≡ L + S. The resulting L-S eigenstates are characterized by term symbols.

As an example we consider the excited helium atom in the atomic electron configuration 2p3p. By the triangular conditions the one-electron spins s = ½ can couple to |½−½|,  ½+½ = 0,  1 (spin singlet and triplet) and the two orbital angular momenta l = 1 can couple to L = |1−1|, 1, 1+1 = 0, 1, 2. In total, Russell-Saunders coupling gives two-electron states labeled by the term symbols:

¹S, ¹P, ¹D, ³S, ³P, ³D,

The dimension is 1×(1+3+5) + 3×(1+3+5) = 36. The electronic configuration 2p3p stands for 6×6 = 36 orbital products, as each of the three p-orbitals has two spin functions, so that in total there are 6 spinorbitals with principal quantum number n = 2 and also 6 spinorbitals with n = 3. A check on dimensions before and after coupling is useful because it is easy to overlook coupled states.

Russell-Saunders coupling gives useful first-order states in the case that one-electron spin-orbit coupling is much less important than the Coulomb interactions between the electrons and can be neglected. This occurs for the low Z part (i.e., the lighter elements) of the periodic table, roughly up to the lanthanoids (previously lanthanides, starting at Z = 57) . The usefulness stems from the fact that states of different L and S do not mix under the total Coulomb interaction, so that L-S coupling achieves a considerable block diagonalization of the matrix of a Hamiltonian in which spin-orbit coupling is absent.

In the high Z regions of the periodic system it is common to first couple the one-electron momenta j ≡ l + s and then the one-electron j-eigenstates to total J. This so-called j-j coupling scheme gives a more useful first-order approximation when spin-orbit interaction is larger than the Coulomb interaction and spin-orbit interaction is included, while the Coulomb interaction is neglected. If, however, in either coupling scheme all resulting states are accounted for, i.e., the same subspace of Hilbert (function) space is obtained, then the choice of coupling scheme is irrelevant in calculations where both interactions—electrostatic and spin-orbit—are included on equal footing.

More complicated electron configurations

Spin branching diagram. Number of electrons n on the abscissa. Spin quantum number S on the ordinate.

Spin coupling

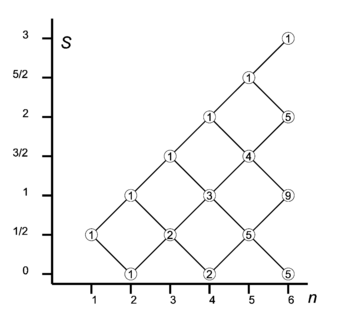
Let us consider how to couple n spin-½ particles (electrons) to eigenstates of total S².

The one-electron system (n = 1) has two functions with s = ½ and m = ± ½ (spin up and down). We have seen that addition of an electron leads to four two-electron spin functions: a singlet (2S + 1 = 1) and a triplet space (a "ladder" of 2S + 1 = 3 spin functions). If we add one spin to the two-electron triplet (S = 1), the triangular conditions tell us that S = 3/2, and S = 1/2 can be obtained. In the diagram on the right we see that two lines depart from the n = 2, S = 1 node. One line goes up and joins the n = 3, S = 3/2 node, the other goes down and joins the n = 3, S = 1/2 node.

A two-particle spin system also has a spin-singlet S = 0. Adding a spin to it leads to a doublet, S = 1/2. It can be shown that the doublet thus obtained is orthogonal to the doublet with the intermediate (n = 2, S = 1) spin triplet. Two different paths lead two different—even orthogonal—three-electron spin doublets. This is why the number 2 is listed in the circle at the n = 3, S = 1/2 node.

From the two doublets we can, by again adding one electron, create two four-electron singlets, and two four-electron triplet spaces (ladders). A four-electron triplet space can also be obtained from the three-electron quadruplet (S = 3/2) by subtracting S = 1/2. Hence we see the number 3 at the n = 4, S = 1 node. It is the sum of numbers in the nodes directly on its left connected to it.

The system of sequentially coupling one electron at the time should be clear now. Every path in the branching diagram corresponds to a unique (2S+1)-dimensional ladder of eigenfunctions of total spin angular momentum operator S² with spin quantum number S. Ladders belonging to different paths are orthogonal. The number in the circle indicates how many paths have this node as endpoint.

It is of interest to check dimensions. For instance, the total spin space of five electrons is of dimension 2⁵ = 32. Reading from bottom to top in the diagram, we find 5×2 + 4×4 + 1×6 (second factors being 2S+1), which indeed adds up to 32.

The actual coupling of electron n to a state of n − 1 electrons uses special values of Clebsch-Gordan coefficients. Let us use k as a path index (e.g., for S = 1 and n = 6, the index k runs from 1 to 9). Then addition (line upwards) gives the n-electron spin state:

$|k,S,M\rangle ={\sqrt {\frac {1}{2S}}}{\Big (}{\sqrt {S+M}}\,|k,S-{\tfrac {1}{2}},M-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle +{\sqrt {S-M}}\,|k,S-{\tfrac {1}{2}},M+{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle {\Big )}.$

Subtraction (line downwards) gives the n-electron spin state:

${\begin{aligned}|k,S,M\rangle =&{\sqrt {\frac {1}{2S+2}}}{\Big (}-{\sqrt {S-M+1}}\,|k,S+{\tfrac {1}{2}},M-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle \\&\quad +{\sqrt {S+M+1}}|k,S+{\tfrac {1}{2}},M+{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle {\Big )}\end{aligned}}$

In particular, for n = 2 we find the spin triplet:

$|1,1,M\rangle ={\sqrt {\frac {1}{2}}}{\Big (}{\sqrt {1+M}}\,|1,{\tfrac {1}{2}},M-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle +{\sqrt {1-M}}\,|1,{\tfrac {1}{2}},M+{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle {\Big )},$

which gives the triplet "ladder", where we suppress in the notation the index k = 1,

${\begin{aligned}|1,1\rangle &=|{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle \equiv \alpha (1)\alpha (2)\\|1,0\rangle &={\sqrt {\tfrac {1}{2}}}{\Big (}|{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle +|{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle {\Big )}\equiv {\sqrt {\tfrac {1}{2}}}{\Big (}\beta (1)\alpha (2)+\alpha (1)\beta (2){\Big )}\\|1,-1\rangle &=|1,{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle \equiv \beta (1)\beta (2)\end{aligned}}$

Here the more common notation for one-electron spin functions (α for m = ½ and β for m = −½) is introduced. Note that all three triplet spin functions are symmetric under interchange of the two electrons.

The two-electron spin singlet follows from (suppressing the path index k = 1 again):

$|0,0\rangle ={\sqrt {\tfrac {1}{2}}}{\Big (}-|{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle +|{\tfrac {1}{2}},{\tfrac {1}{2}}\rangle |{\tfrac {1}{2}},-{\tfrac {1}{2}}\rangle {\Big )}\equiv {\sqrt {\tfrac {1}{2}}}{\Big (}\alpha (1)\beta (2)-\beta (1)\alpha (2){\Big )}$

a function that is antisymmetric (changes sign) under permutation of electron 1 and 2.

Orbital coupling

The one-electron orbital angular momenta l can also be coupled sequentially, i.e., one after the other. Different paths give orthogonal states. Consider as an example the configuration p³. Repeated application of the triangular conditions gives that 3³ = 27 dimensional space decomposes as follows in eigenspaces of L², [with L ≡ l(1) + l(2)+ l(3) ]:

(2)F,   (2)D,   (1)D,   (2)P,   (1)P,   (0)P,   (1)S

where the two-electron quantum numbers L₁₂ of electron 1 and 2 precede in brackets the letters designating the three-electron angular momentum quantum number. Dimensions are: 7 + 5 + 5 + 3 + 3 + 3 + 1 = 27. We see that there are two orthogonal D spaces and three orthogonal P spaces, while there is only one F and S space (of dimension 7 and 1, respectively).

The algorithm should be clear now. For instance, to decompose the 135-dimensional space belonging to the configuration p³d, one can use the result for p³ and add d to any of the eigenspaces and use the triangular conditions again, as in F × d gives L = 5, 4, 3, 2, 1.

Pauli principle

So far we ignored the Pauli principle that states that more-electron wave functions must be antisymmetric under simultaneous transposition of spatial and spin coordinates of any pair of electrons. This principle affects considerably the results for configurations of equivalent electrons, which by definition are electrons with the same n (principal) and l (azimuthal or angular momentum) quantum numbers. We will see that certain multiplets (LS states) arising from equivalent electrons are forbidden by the Pauli principle. Multiplets arising from non-equivalent electrons are never forbidden, they simply give rise to non-vanishing antisymmetric states.

Let us take as an example the spatial product, describing two equivalent electrons, 2p_x(1)2p_x(2). We have seen that there are two-electron singlet and triplet spin functions. In both cases we look at M_S = 0 functions, thus,

${\begin{aligned}|p_{x}^{2},S=0,M_{S}=0\rangle &\equiv 2p_{x}(1)2p_{x}(2){\Big (}\alpha (1)\beta (2)-\beta (1)\alpha (2){\Big )}/{\sqrt {2}}\\|p_{x}^{2},S=1,M_{S}=0\rangle &\equiv 2p_{x}(1)2p_{x}(2){\Big (}\alpha (1)\beta (2)+\beta (1)\alpha (2){\Big )}/{\sqrt {2}}\\\end{aligned}}$

Antisymmetric functions, satisfying the Pauli principle, are obtained by use of the antisymmetrizer $\scriptstyle {\mathcal {A}}=[(1)-(12)]/2$, where (12) transposes space and spin coordinates of electron 1 and 2 and (1) is the identity operator (does nothing).

${\begin{aligned}2{\mathcal {A}}|p_{x}^{2},S=0,M_{S}=0\rangle &=2p_{x}(1)2p_{x}(2){\Big (}\alpha (1)\beta (2)-\beta (1)\alpha (2){\Big )}/{\sqrt {2}}\\&-2p_{x}(2)2p_{x}(1){\Big (}\alpha (2)\beta (1)-\beta (2)\alpha (1){\Big )}/{\sqrt {2}}\\&=2\left[2p_{x}(1)2p_{x}(2){\Big (}\alpha (1)\beta (2)-\beta (1)\alpha (2){\Big )}/{\sqrt {2}}\right]\\\end{aligned}}$

Hence

${\mathcal {A}}|p_{x}^{2},S=0,M_{S}=0\rangle =|p_{x}^{2},S=0,M_{S}=0\rangle$

The symmetric spatial function 2p_x(1)2p_x(2) multiplied by the antisymmetric spin singlet function is an eigenfunction of the antisymmetrizer, that is, the space-spin product satisfies the Pauli principle.

We repeat the calculation for the spin triplet

${\begin{aligned}2{\mathcal {A}}|p_{x}^{2},S=1,M_{S}=0\rangle &=2p_{x}(1)2p_{x}(2){\Big (}\alpha (1)\beta (2)+\beta (1)\alpha (2){\Big )}/{\sqrt {2}}\\&-2p_{x}(2)2p_{x}(1){\Big (}\alpha (2)\beta (1)+\beta (2)\alpha (1){\Big )}/{\sqrt {2}}\\&=0\\\end{aligned}}$

Hence

${\mathcal {A}}|p_{x}^{2},S=1,M_{S}=0\rangle =0$

The symmetric spatial function 2p_x(1)2p_x(2) multiplied by the symmetric spin triplet function does not have an antisymmetric component, that is, this space-spin product is forbidden by the Pauli principle.

In general one can show from the symmetry of the Clebsch-Gordan coefficients that eigenstates of L² for two equivalent electrons with odd quantum number L are antisymmetric under transposition of the electron coordinates. Hence these odd L states must be multiplied by symmetric spin functions (triplets S = 1). In total L+S must be even.

The even L states (we are considering still two equivalent electrons) are even under transposition and must be multiplied by odd spin functions (singlets, S = 0). Again L+S must be even in order to get a non-vanishing result upon antisymmetrization.

Before continuing, it must be pointed out that there exists an interesting symmetry between holes and particles. We call an atomic subshell (a set of orbitals with a given principal quantum number n and a given l ) closed, if there are 2(2l+1) electrons in the subshell. For instance the 2p subshell in the neon atom contains 6 electrons and hence it is closed. Likewise in the cupper atom the 3d subshell is closed (contains 10 electrons). Such a closed subshell has in common with a vacuum that it is an eigenstate of L² and S² with L = S = 0. (The non-trivial proof of this fact is skipped). It is sometimes called a Fermi vacuum. If we remove an electron from a closed subshell we make a hole in it. It can be shown that a hole shares many properties with an electron: it has the same orbital and spin angular momentum quantum number. A number of holes must satisfy the Pauli principle in the very same way as an equal number of electrons.

We formulated the rule: L + S must be even for two equivalent electrons. This rule also holds for two equivalent holes. Thus, for instance the carbon atom ground state has two equivalent electrons: 1s²2s²2p², which gives ³P, ¹D and ¹S. The oxygen atom ground state has two equivalent holes: 1s²2s²2p⁴, which also gives ³P, ¹D and ¹S.

Knowing all this we can construct the following table

${\begin{aligned}(ns)^{2}\rightarrow \quad &^{1}S\\(np)^{2},(np)^{4}\rightarrow \quad &^{1}S,\,^{1}D,\,^{3}P\\(nd)^{2},(nd)^{8}\rightarrow \quad &^{1}S,\,^{1}D,\,^{1}G,\,^{3}P,\,^{3}F\\(nf)^{2},(nf)^{12}\rightarrow \quad &^{1}S,\,^{1}D,\,^{1}G,\,^{1}I,\,^{3}P,\,^{3}F,\,^{3}H\\\end{aligned}}$

For more than two electrons (or holes) the theory can be extended. It can be shown that an N-electron function belongs to an irreducible representation of the symmetric group (also known as permutation group) S_N. In other words, the concept of symmetry and antisymmetry under transposition can be generalized to more than two particles. This generalized permutation symmetry is enforced on the spin functions by requiring them to be eigenfunctions of S², a Casimir operator of the group SU(2). The irreducible representations of SU(2) and S² are intertwining. The antisymmetrizer acting on an orbital product times an eigenfunction of S² enforces permutational symmetry on the orbital product. The permutational symmetry of the orbital product, finally, implies that the orbital product is adapted to the unitary group U(2l+1). The irreducible representations of the latter group carry different eigenstates of L², which, by construction, are Pauli allowed.