Platonic solid

In geometry, a convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a Platonic solid. There are only five Platonic solids, shown in the table below:

number of faces	name	type of face	volume	surface area	properties	image
4	regular tetrahedron (or regular triangular pyramid)	equilateral triangle	${\tfrac {\sqrt {2}}{12}}s^{3}$	${\sqrt {3}}s^{2}$	4 vertices, 6 edges, self-dual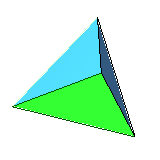
6	cube	square	$s^{3}$	$6s^{2}$	8 vertices, 12 edges, dual to octahedron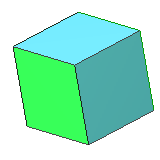
8	regular octahedron	equilateral triangle	${\tfrac {\sqrt {2}}{3}}s^{3}$	$2{\sqrt {3}}s^{2}$	6 vertices, 12 edges, dual to cube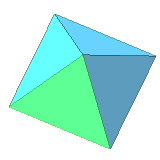
12	regular dodecahedron	regular pentagon	${\tfrac {15+7{\sqrt {5}}}{4}}s^{3}$	$3{\sqrt {25+10{\sqrt {5}}}}s^{2}$	20 vertices, 30 edges, dual to icosahedron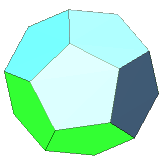
20	regular icosahedron	equilateral triangle	${\tfrac {15+5{\sqrt {5}}}{12}}s^{3}$	$5{\sqrt {3}}s^{2}$	12 vertices, 30 edges, dual to dodecahedron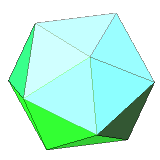

The dual of a polyhedron is the polyhedron formed by taking the center of each face as the vertex of the dual. The regular tetrahedron is self-dual - connecting the center of each face results in a smaller tetrahedron. The cube and regular octahedron are dual to each other, and the regular dodecahedron and icosahedron are dual to each other.

A sphere circumscribed about any of the Platonic solids will touch all the vertices, and a sphere inscribed within any will touch all the faces at the center of the face.

Proof that there are only 5 Platonic solids

Proving that there are only 5 Platonic solids is rather easy: From the definition, the faces must be regular polygons which can meet three or more at a point with some excess angle, to create a solid angle. Any regular polygon with 7 or more sides cannot meet three or more to a point without overlapping. The regular hexagon can meet three at a point, but with no excess, thus no solid angle is formed. That leaves the regular pentagon, the square, and the equilateral triangle as the only possible faces for a Platonic solid. The regular pentagon and the square can only meet three at a point and have any excess to allow forming a solid angle. The Platonic solids thus formed are the dodecahedron and the cube. The equilateral triangle can meet three, four, or five at a point and form a solid angle; the figures formed are the tetrahedron, octahedron, and icosahedron, respectively.