Exponential function: Difference between revisions
imported>Dmitrii Kouznetsov (→Generalization of exponential: add figure. refs.) |
imported>Richard Pinch (copyediting; added dates, ref) |
||
| Line 1: | Line 1: | ||
'''Exponential function''' or exp, can be defined as solution of differential | '''Exponential function''' or exp, can be defined as solution of differential equation | ||
: <math> \exp^{\prime}(z)=\exp(z)</math> | : <math> \exp^{\prime}(z)=\exp(z)</math> | ||
with additional condition | with the additional condition | ||
: <math> \exp(0)=1 </math> | : <math> \exp(0)=1 </math> | ||
The study of the exponential function began with [[Leonhard Euler]] around 1730<ref>William Dunham, ''Euler, the Master of us all'', MAA (1999) ISBN 0-8835-328-0. Pp.17-37.</ref> | |||
Since that time, it | Since that time, it has had widely applications in technology and science; in particular, [[exponential growth]] is described with such functions. | ||
is described with such | |||
==Properties== | ==Properties== | ||
The exponential is an [[entire function]]. | |||
For any | For any complex <math>p</math> and <math>q</math>, the basic property holds: | ||
: <math> \exp(a)~\exp(b)=\exp(a+b) </math> | : <math> \exp(a)~\exp(b)=\exp(a+b) </math> | ||
The definition allows to calculate all the | The definition allows to calculate all the derivatives at zero; so, the [[Taylor expansion]] has the form | ||
: <math> \exp(z)=\sum_{n=0}^\infty \frac{z^n}{n!} ~ ~ \forall z\in \mathbb{C} </math> | : <math> \exp(z)=\sum_{n=0}^\infty \frac{z^n}{n!} ~ ~ \forall z\in \mathbb{C} </math> | ||
where <math>\mathbb{C}</math> means the set of [[complex number]]s. | where <math>\mathbb{C}</math> means the set of [[complex number]]s. | ||
The series converges for | The series converges for any complex <math>z</math>. In particular, the series converges for any real value of the argument. | ||
==Inverse function== | ==Inverse function== | ||
The inverse function of the exponential is the [[logarithm]]; for any complex <math>z\ne 0</math>, the relation holds: | |||
: <math> \exp(\log(z))=z ~ \forall z\in \mathbb{C} </math> | : <math> \exp(\log(z))=z ~ \forall z\in \mathbb{C} </math> | ||
| Line 28: | Line 27: | ||
: <math> \log(\exp(z))=z ~ \forall z\in \mathbb{C} ~ \mathrm{~ such ~ that ~ } |\Im(z)|<\pi </math> | : <math> \log(\exp(z))=z ~ \forall z\in \mathbb{C} ~ \mathrm{~ such ~ that ~ } |\Im(z)|<\pi </math> | ||
When the logarithm has a cut along the negative part of the real axis, exp can be considered. | |||
==Number e == | ==Number e == | ||
| Line 36: | Line 35: | ||
==Relation with [[sin]] and [[cos]] functions== | ==Relation with [[sin]] and [[cos]] functions== | ||
The exponential is related to the [[trigonometric function]]s [[sine]] and [[cosine]] by ''[[de Moivre]]'s formula'': | |||
: <math> \exp(\mathrm{i} z) = \cos(z)+\mathrm{i} \sin(z) ~ \forall z\in \mathbb{C} </math> | : <math> \exp(\mathrm{i} z) = \cos(z)+\mathrm{i} \sin(z) ~ \forall z\in \mathbb{C} </math> | ||
| Line 44: | Line 44: | ||
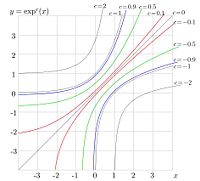
[[Image:Expc.jpg|right|200px|thumb|<math>\exp^c(x)</math> versus <math>x</math> for some real values of <math>c</math>.]] | [[Image:Expc.jpg|right|200px|thumb|<math>\exp^c(x)</math> versus <math>x</math> for some real values of <math>c</math>.]] | ||
The notation <math>\exp_b</math> is used for the exponential with scaled argument; | |||
: <math>\exp_b(z)=b^z=\exp(\log(b) z)</math> | : <math>\exp_b(z)=b^z=\exp(\log(b) z)</math> | ||
| Line 69: | Line 69: | ||
: <math>F^{-1}\Big (F(z)\Big)=z</math> | : <math>F^{-1}\Big (F(z)\Big)=z</math> | ||
If in the notation <math>\exp_b^c</math> superscript is omitted, it is assumed to be unity; for example | If in the notation <math>\exp_b^c</math> the superscript is omitted, it is assumed to be unity; for example | ||
<math>\exp_b^1=\exp_b</math>. If the | <math>\exp_b^1=\exp_b</math>. If the suberscript is omitted, it is assumed to be <math>\mathrm{e}</math>, id est, <math>\exp^c=\exp_\mathrm{e}^c</math> | ||
<math>\exp^c=\exp_\mathrm{e}^c</math> | |||
==References== | ==References== | ||
{{reflist}} | |||
* Ahlfors, Lars V. (1953). Complex analysis. McGraw-Hill Book Company, Inc.. | * Ahlfors, Lars V. (1953). Complex analysis. McGraw-Hill Book Company, Inc.. | ||
* H.Kneser. ``Reelle analytische L\"osungen der Gleichung <math>\varphi(\varphi(x))=\mathrm{e}^{x}</math> | * H.Kneser. ``Reelle analytische L\"osungen der Gleichung <math>\varphi(\varphi(x))=\mathrm{e}^{x}</math> | ||
und verwandter Funktionalgleichungen''. Journal f\"ur die reine und angewandte Mathematik, <b> 187</b> (1950), 56-67. | und verwandter Funktionalgleichungen''. Journal f\"ur die reine und angewandte Mathematik, <b> 187</b> (1950), 56-67. | ||
[[Category: | [[Category:Functions]] | ||
[[Category:Mathematica | [[Category:Mathematica functions]] | ||
Revision as of 01:22, 29 October 2008
Exponential function or exp, can be defined as solution of differential equation
with the additional condition
The study of the exponential function began with Leonhard Euler around 1730[1] Since that time, it has had widely applications in technology and science; in particular, exponential growth is described with such functions.
Properties
The exponential is an entire function.
For any complex and , the basic property holds:
The definition allows to calculate all the derivatives at zero; so, the Taylor expansion has the form
where means the set of complex numbers. The series converges for any complex . In particular, the series converges for any real value of the argument.
Inverse function
The inverse function of the exponential is the logarithm; for any complex , the relation holds:
Exponential also can be considered as inverse of logarithm, while the imaginary part of the argument is smaller than :
When the logarithm has a cut along the negative part of the real axis, exp can be considered.
Number e
is widely used in applications; this notation is commonly accepted. Its approximate value is
- Failed to parse (syntax error): {\displaystyle {\rm e}=\exp(1) \approx 2.71828 18284 59045 23536}
Relation with sin and cos functions
The exponential is related to the trigonometric functions sine and cosine by de Moivre's formula:
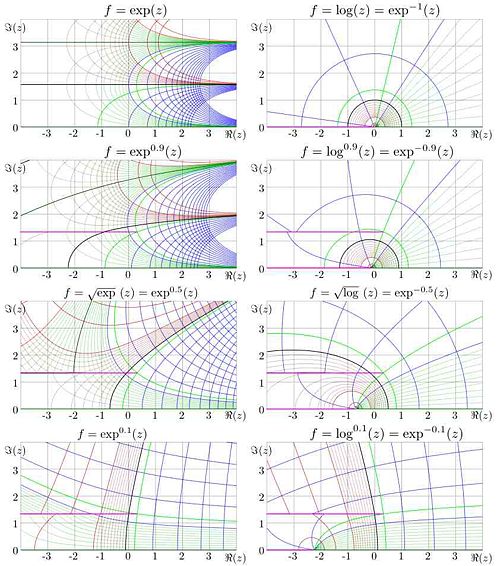
Generalization of exponential
The notation is used for the exponential with scaled argument;
Notation is used for the iterated exponential:
For non-integer values of , the iterated exponential can be defined as
where is function satisfying conditions
The inverse function is defined with condition
and, within some range of values of
If in the notation the superscript is omitted, it is assumed to be unity; for example . If the suberscript is omitted, it is assumed to be , id est,
References
- ↑ William Dunham, Euler, the Master of us all, MAA (1999) ISBN 0-8835-328-0. Pp.17-37.
- Ahlfors, Lars V. (1953). Complex analysis. McGraw-Hill Book Company, Inc..
- H.Kneser. ``Reelle analytische L\"osungen der Gleichung
und verwandter Funktionalgleichungen. Journal f\"ur die reine und angewandte Mathematik, 187 (1950), 56-67.