Rhombus: Difference between revisions
Jump to navigation
Jump to search

imported>Anthony Argyriou (fix a little) |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
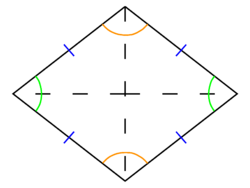
{{Image|Rhombus.png|right|250px|A ''rhombus''. All sides (marked blue) are of equal length; opposite angles (same color arc) are equal; diagonals cross at right angles.}} | |||
A '''rhombus''' is a [[polygon]] of four sides of equal length. The angles of each pair of opposite vertices are equal. A rhombus is a special case of a [[parallelogram]] where all four sides are of equal length. A [[square]] is a special case of rhombus, where all four vertex angles are equal. | A '''rhombus''' is a [[polygon]] of four sides of equal length. The angles of each pair of opposite vertices are equal. A rhombus is a special case of a [[parallelogram]] where all four sides are of equal length. A [[square]] is a special case of rhombus, where all four vertex angles are equal. | ||
==Properties== | ==Properties== | ||
As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees; as with a parallelogram, it can be shown that the angles of opposite pairs of vertices are equal. | As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees; as with a parallelogram, it can be shown that the angles of opposite pairs of vertices are equal. | ||
Revision as of 10:25, 19 November 2009
A rhombus is a polygon of four sides of equal length. The angles of each pair of opposite vertices are equal. A rhombus is a special case of a parallelogram where all four sides are of equal length. A square is a special case of rhombus, where all four vertex angles are equal.
Properties
As with all quadrilaterals, the sum of the interior angles of a rhombus is 360 degrees; as with a parallelogram, it can be shown that the angles of opposite pairs of vertices are equal.
The perimeter of a rhombus is equal to 4 times the length of one side. The area of a square is equal to the length of the side multiplied by itself, multiplied by the sine of the angle between the sides.[1]
Any rhombus can tile a plane with no voids.
- ↑ Since the sum of the four angles is 360 degrees, and pairs of angles are equal, the sum of the angles of two adjacent vertices is 180 degrees. Since sin(180-x)=sin(x), the formula produces the same result no matter which vertex angle is chosen.