Reflection (geometry): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 5: | Line 5: | ||
\sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | \sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | ||
</math> | </math> | ||
The operation σ is orthogonal, i.e., preserves inner products, so that | The operation σ is [[orthogonal]], i.e., preserves inner products, so that | ||
:<math> | :<math> | ||
\sigma^\mathrm{T} = \sigma^{-1} = \sigma. \, | \sigma^\mathrm{T} = \sigma^{-1} = \sigma. \, | ||
</math> | </math> | ||
Hence reflection is orthogonal and [[symmetric]]. Further it has [[determinant]] −1. Because σ is symmetric it has real eigenvalues; since it is orthogonal its eigenvalues have modulus 1. In other words its eigenvalues are ±1. The product of the eigenvalues being the determinant (−1), the eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is minus the identity operator, this operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the first set of eigenvalues is reflection in a plane. Reflection in a plane will be considered further in this article. | |||
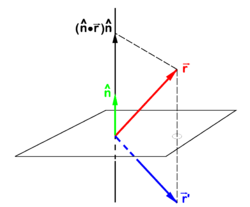
{{Image|Reflection in plane.png|right|250px|Fig. 1. The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | {{Image|Reflection in plane.png|right|250px|Fig. 1. The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | ||
==Reflection in a plane== | ==Reflection in a plane== | ||
Revision as of 23:46, 19 July 2009
In analytic geometry, a reflection is a linear operation σ on with σ2 = 1, i.e., σ is an involution, and σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :
The operation σ is orthogonal, i.e., preserves inner products, so that
Hence reflection is orthogonal and symmetric. Further it has determinant −1. Because σ is symmetric it has real eigenvalues; since it is orthogonal its eigenvalues have modulus 1. In other words its eigenvalues are ±1. The product of the eigenvalues being the determinant (−1), the eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is minus the identity operator, this operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the first set of eigenvalues is reflection in a plane. Reflection in a plane will be considered further in this article.
Reflection in a plane
If is a unit vector normal (perpendicular) to a plane—the mirror plane—then is the projection of on this unit vector. From the figure it is evident that
If a non-unit normal is used then substitution of
gives the mirror image,
This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,
and let v be an element of the one-dimensional space V1 then the involution
is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.
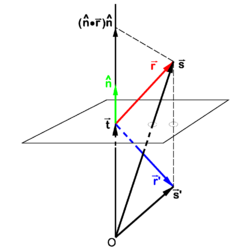
Reflection in plane not through origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector . The length of this vector is the distance from O to the plane. From Figure 2, we find
Use of the equation derived earlier gives
And hence the equation for the reflected pair of vectors is,
where is a unit normal to the plane. Obviously and are proportional, differ by a scaling.
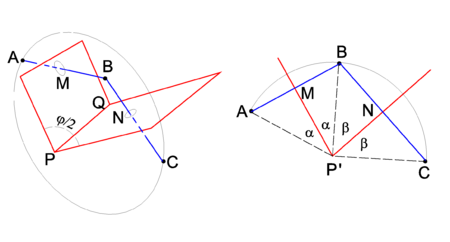
Two consecutive reflections
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an orthogonal matrix with determinant −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det(AB) = det(A)det(B), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation.