Reflection (geometry): Difference between revisions
imported>Paul Wormer (New page: In analytic geometry, a '''reflection''' is a linear operation σ on a vector space with σ<sup>2</sup> = 1, i.e., σ is an ''involution''. Reflecting twice an arbitrar...) |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | |||
In [[analytic geometry]], a '''reflection''' is a linear operation σ on a vector space with σ<sup>2</sup> = 1, i.e., σ is an ''involution''. Reflecting twice an arbitrary vector brings back the original vector : | In [[analytic geometry]], a '''reflection''' is a linear operation σ on a vector space with σ<sup>2</sup> = 1, i.e., σ is an ''involution''. Reflecting twice an arbitrary vector brings back the original vector : | ||
:<math> | :<math> | ||
Revision as of 07:17, 18 July 2009
In analytic geometry, a reflection is a linear operation σ on a vector space with σ2 = 1, i.e., σ is an involution. Reflecting twice an arbitrary vector brings back the original vector :
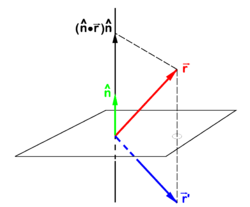
Reflection in a plane
If is a unit vector normal (perpendicular) to a plane—the mirror plane—then is the projection of on this unit vector. From the figure it is evident that
If a non-unit normal is used then substitution of
gives the mirror image,
This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,
and let v be an element of the one-dimensional space V1 then the involution
is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.