Reflection (geometry): Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[analytic geometry]], a '''reflection''' is a linear operation σ on | In [[analytic geometry]], a '''reflection''' is a linear operation σ on <math>\mathbb{R}^3</math> with σ<sup>2</sup> = 1, i.e., σ is an ''involution'', and | ||
σ<sup>−1</sup> = σ. Reflecting twice an arbitrary vector brings back the original vector : | |||
:<math> | :<math> | ||
\sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | \sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | ||
</math> | </math> | ||
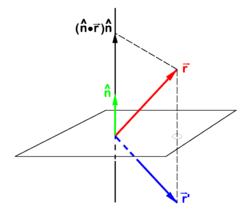
{{Image|Reflection in plane.png|right|250px|The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | The operation σ is orthogonal, i.e., preserves inner products, so that | ||
:<math> | |||
\sigma^\mathrm{T} = \sigma^{-1} = \sigma. \, | |||
</math> | |||
Reflection is orthogonal and symmetric. | |||
{{Image|Reflection in plane.png|right|250px|Fig. 1. The vector <math>\scriptstyle \vec{\mathbf{r}}</math> goes to <math>\scriptstyle\vec{\mathbf{r}}'</math> under reflection in a plane. The unit vector <math>\scriptstyle\hat{\mathbf{n}}</math> is normal to mirror plane. }} | |||
==Reflection in a plane== | ==Reflection in a plane== | ||
If <math>\hat{\mathbf{n}}</math> is a unit vector normal (perpendicular) to a plane—the mirror plane—then <math> (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\hat{\mathbf{n}}</math> is the projection of <math>\vec{\mathbf{r}}</math> on this unit vector. From the figure it is evident that | If <math>\hat{\mathbf{n}}</math> is a unit vector normal (perpendicular) to a plane—the mirror plane—then <math> (\hat{\mathbf{n}}\cdot\vec{\mathbf{r}})\hat{\mathbf{n}}</math> is the projection of <math>\vec{\mathbf{r}}</math> on this unit vector. From the figure it is evident that | ||
:<math> | :<math> | ||
| Line 28: | Line 36: | ||
</math> | </math> | ||
is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | is a reflection of ''r'' in the ''hyperplane'' ''V''<sub>''m−1''</sub>. (By definition a hyperplane is an ''m−1''-dimensional linear subspace of a linear space of dimension ''m''.) The inner product of two vectors ''v'' and ''w'' is notated as (''v'', ''w''), which is common for vector spaces of arbitrary dimension. | ||
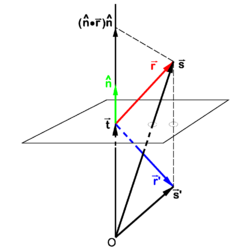
{{Image|Reflection shifted plane.png|left|250px|Fig. 2. The vector <math>\vec{\mathbf{s}}</math> goes to <math>\vec{\mathbf{s}}\,'</math> under reflection}} | |||
==Reflection in plane not through origin== | |||
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector <math>\vec{\mathbf{t}}</math>. The length of this vector is the distance from O to the plane. | |||
From Figure 2, we find | |||
:<math> | |||
\vec{\mathbf{r}} = \vec{\mathbf{s}} - \vec{\mathbf{t}}, \quad | |||
\vec{\mathbf{r}}\,' = \vec{\mathbf{s}}\,' - \vec{\mathbf{t}} | |||
</math> | |||
Use of the equation derived earlier gives | |||
:<math> | |||
\vec{\mathbf{s}}\,' - \vec{\mathbf{t}} = \vec{\mathbf{s}} - \vec{\mathbf{t}} | |||
- 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}. | |||
</math> | |||
And hence the equation for the reflected pair of vectors is, | |||
:<math> | |||
\vec{\mathbf{s}}\,' = \vec{\mathbf{s}} | |||
- 2 \big(\hat{\mathbf{n}}\cdot (\vec{\mathbf{s}} - \vec{\mathbf{t}})\big)\hat{\mathbf{n}}, | |||
</math> | |||
where <math>\hat{\mathbf{n}}</math> is a unit normal to the plane. Obviously <math>\vec{\mathbf{t}}</math> and <math>\hat{\mathbf{n}}</math> are proportional, differ by a scaling. | |||
==Two consecutive reflections== | ==Two consecutive reflections== | ||
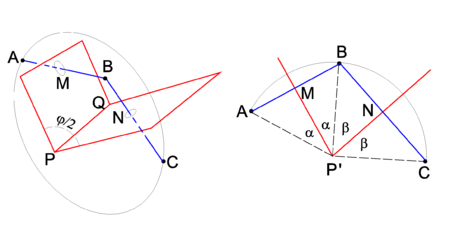
{{Image|Two reflections.png|right|450px|Fig. | {{Image|Two reflections.png|right|450px|Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′}} | ||
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. | Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. | ||
The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2. | The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2. | ||
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an [[orthogonal matrix]] with [[determinant]] −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det('''AB''') = det('''A''')det('''B'''), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation. | From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an [[orthogonal matrix]] with [[determinant]] −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det('''AB''') = det('''A''')det('''B'''), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation. | ||
Revision as of 10:32, 19 July 2009
In analytic geometry, a reflection is a linear operation σ on with σ2 = 1, i.e., σ is an involution, and σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :
The operation σ is orthogonal, i.e., preserves inner products, so that
Reflection is orthogonal and symmetric.
Reflection in a plane
If is a unit vector normal (perpendicular) to a plane—the mirror plane—then is the projection of on this unit vector. From the figure it is evident that
If a non-unit normal is used then substitution of
gives the mirror image,
This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,
and let v be an element of the one-dimensional space V1 then the involution
is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.
Reflection in plane not through origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector . The length of this vector is the distance from O to the plane. From Figure 2, we find
Use of the equation derived earlier gives
And hence the equation for the reflected pair of vectors is,
where is a unit normal to the plane. Obviously and are proportional, differ by a scaling.
Two consecutive reflections
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an orthogonal matrix with determinant −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det(AB) = det(A)det(B), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation.