Great circle: Difference between revisions
imported>Paul Wormer m (New page: {{subpages}} {{Image|Great_circle.png|right|350px|Great circle. The green arc is part of a great circle that connects the points '''r'''<sub>1</sub> and '''r'''<sub>2</sub> on the surface ...) |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
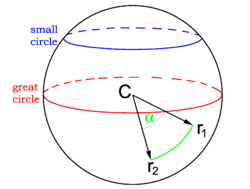
{{Image|Great_circle.png|right| | {{Image|Great_circle.png|right|250px|Great circle. The green arc is part of a great circle that connects the points '''r'''<sub>1</sub> and '''r'''<sub>2</sub> on the surface of the sphere. It is the shortest distance between the points.}} | ||
A '''great circle''' of a sphere is the intersection of the surface of the sphere with a plane passing through the center ''C'' of the sphere. The [[radius]] of a great circle is equal to the radius of the sphere. The center of the great circle coincides with the center of the sphere. An intersection plane that does not pass through the center of the sphere cuts off a circle that is smaller (has a smaller radius). | A '''great circle''' of a sphere is the intersection of the surface of the sphere with a plane passing through the center ''C'' of the sphere. The [[radius]] of a great circle is equal to the radius of the sphere. The center of the great circle coincides with the center of the sphere. | ||
A great circle cuts a sphere into two equal hemispheres. An intersection plane that does not pass through the center of the sphere cuts off a circle that is smaller (has a smaller radius). | |||
It can be proved that a great circle passing through two points is a [[ | It can be proved that a great circle passing through two points is a [[geodesic]], a line of shortest distance connecting the two points. In the figure we see a plane spanned by two vectors ('''r'''<sub>1</sub> and '''r'''<sub>2</sub>) that passes through ''C''. Hence the green arc is part of the great circle connecting the two points and is the shortest distance between the points. | ||
It is not difficult to find an expression for the angle α | It is not difficult to find an expression for the angle α. The length of the green arc is the radius of the great circle times this angle. Write in [[spherical polar coordinates]] the [[dot product]] | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 13: | Line 14: | ||
r\cos\phi_2\sin\theta_2\\ r\sin\phi_2\sin\theta_2\\ r\cos\theta_2 | r\cos\phi_2\sin\theta_2\\ r\sin\phi_2\sin\theta_2\\ r\cos\theta_2 | ||
\end{pmatrix} \\ | \end{pmatrix} \\ | ||
&= r^2 \ | &= r^2 \cos(\phi_1-\phi_2)\sin\theta_1\sin\theta_2 + r^2\cos\theta_1\cos\theta_2, | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 19: | Line 20: | ||
Now clearly | Now clearly | ||
:<math> | :<math> | ||
\alpha = \arccos \big(\ | r\alpha = r\arccos \big(\cos(\phi_1-\phi_2)\sin\theta_1\sin\theta_2 + \cos\theta_1\cos\theta_2 \big)\, | ||
</math> | </math> | ||
is the required arc length. | is the required arc length. | ||
==Example== | |||
If we assume that the Earth is a perfect sphere of radius 6378 km it is not difficult to find the distance between [[London]] and [[Los Angeles]]. London is at 51°30′N, 0°08′W and Los Angeles is at 34°03′N, 118°15′W. The spherical polar angles are (38.5°, 0.1333°) and (55.95°, 118.25°), respectively. The angle α = 78.7481° and the distance is 8766 km. If we could go through the Earth in a straight line (Euclidean metric) the distance would be 8092 km. | |||
Revision as of 10:21, 3 September 2009
A great circle of a sphere is the intersection of the surface of the sphere with a plane passing through the center C of the sphere. The radius of a great circle is equal to the radius of the sphere. The center of the great circle coincides with the center of the sphere. A great circle cuts a sphere into two equal hemispheres. An intersection plane that does not pass through the center of the sphere cuts off a circle that is smaller (has a smaller radius).
It can be proved that a great circle passing through two points is a geodesic, a line of shortest distance connecting the two points. In the figure we see a plane spanned by two vectors (r1 and r2) that passes through C. Hence the green arc is part of the great circle connecting the two points and is the shortest distance between the points.
It is not difficult to find an expression for the angle α. The length of the green arc is the radius of the great circle times this angle. Write in spherical polar coordinates the dot product
where we wrote r for the radius of the sphere and used that this is the length of both vectors. Now clearly
is the required arc length.
Example
If we assume that the Earth is a perfect sphere of radius 6378 km it is not difficult to find the distance between London and Los Angeles. London is at 51°30′N, 0°08′W and Los Angeles is at 34°03′N, 118°15′W. The spherical polar angles are (38.5°, 0.1333°) and (55.95°, 118.25°), respectively. The angle α = 78.7481° and the distance is 8766 km. If we could go through the Earth in a straight line (Euclidean metric) the distance would be 8092 km.