Doppler effect: Difference between revisions
imported>John R. Brews (→Other examples: observation) |
imported>John R. Brews m (→Other examples) |
||
| Line 37: | Line 37: | ||
For a discussion see {{cite book |title=Discovering the Universe: From the Stars to the Planets |author=Neil F. Comins, William J. Kaufmann |url=http://books.google.com/books?id=J1d9HJHlISkC&pg=PA174 |pages=pp. 174 ''ff'' |chapter=§6–12: The orbital motion of binary stars affects the wavelengths of their spectral lines |isbn=1429230428 |year=2008 |publisher=Macmillan}} | For a discussion see {{cite book |title=Discovering the Universe: From the Stars to the Planets |author=Neil F. Comins, William J. Kaufmann |url=http://books.google.com/books?id=J1d9HJHlISkC&pg=PA174 |pages=pp. 174 ''ff'' |chapter=§6–12: The orbital motion of binary stars affects the wavelengths of their spectral lines |isbn=1429230428 |year=2008 |publisher=Macmillan}} | ||
</ref> In this example, the light always propagates | </ref> In this example, the light always propagates in the same direction, and only the separation of the observer and source is changing. | ||
==Notes== | ==Notes== | ||
<references/> | <references/> | ||
Revision as of 08:54, 13 April 2011
The Doppler effect (or Doppler shift, or Doppler's principle), named after Christian Doppler who proposed it in 1842,[1] is the change in frequency of a wave for an observer moving relative to the source of the wave. If the observer and source of wave motion approach each other, the frequency appears higher, and if the observer and the source separate, the frequency appears lower.
Analysis
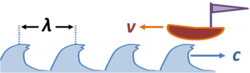
The increase in frequency when moving toward a source can be explained using the figure. Suppose that waves blowing ashore with velocity c are spaced a distance λ apart. Therefore, the time between crests for an observer at a fixed location is λ / c, and the frequency with which a crest appears at a fixed location is fw :
The boat going to sea is running at velocity v in the opposite direction to the waves, and toward the source of the wind. Consequently the boat moves relative to the crests at a speed v+c. That means a crest is met at intervals of time τ :
In other words, the frequency with which the boat bumps over a crest fb is:
so evidently fb is a higher frequency than the frequency fw of the waves themselves. This increase in frequency is the Doppler effect, and it is often expressed as the shift in frequency fd, the Doppler shift, namely:
Of course, if the boat runs inshore with the wave, away from the source of the wind, the opposite happens: it takes the boat longer between crests, and the frequency with which the boat bumps over a crest is lower than the actual frequency of the waves. In particular, if the boat moves at the same speed as the waves (rides the waves into shore) the frequency of bumping over crests drops to zero.
Other examples
The same effect appears when the ear and a police siren move toward each other: the sound of the siren to the ear is pitched higher than the actual pitch of the siren, and when the police pass, so the ear and siren are separating, and the waves from the siren are traveling in the same direction as the ear, the pitch to the ear drops to become lower than the pitch of the siren.[2]
As for binary stars, the case considered by Doppler, as the stars orbit each other, unless they are in a plane perpendicular to the line of sight, they are alternately moving toward and away from the observing astronomer, so the frequency of the light from each star (its color) alternates as well.[3] In this example, the light always propagates in the same direction, and only the separation of the observer and source is changing.
Notes
- ↑ C Doppler (1843). "Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (On the colored light of the binary stars and some other stars of the heavens)". Abhandlungen der koniglich bohmischen Gesellschaft der Wissenschaften vol 2,: pp. 465-482.
- ↑ For a discussion see Theo Koupelis (2010). “§4–7: The Doppler effect”, In Quest of the Universe, 6th ed. Jones & Bartlett Learning, pp. 115 ff. ISBN 0763768588.
- ↑ For a discussion see Neil F. Comins, William J. Kaufmann (2008). “§6–12: The orbital motion of binary stars affects the wavelengths of their spectral lines”, Discovering the Universe: From the Stars to the Planets. Macmillan, pp. 174 ff. ISBN 1429230428.