Relative permeability: Difference between revisions
imported>John R. Brews mNo edit summary |
imported>John R. Brews (→Relation to forces: some math) |
||
| Line 27: | Line 27: | ||
It happens, however, that magnetic poles always occur as opposite pairs, so the force law between single poles cannot be observed directly. However, [[magnetic dipole|''magnetic dipoles'']] do occur in nature and can be directly observed. A planar wire loop conducting a steady electric current resembles a magnetic dipole at distances large compared to the dimensions of the loop. | It happens, however, that magnetic poles always occur as opposite pairs, so the force law between single poles cannot be observed directly. However, [[magnetic dipole|''magnetic dipoles'']] do occur in nature and can be directly observed. A planar wire loop conducting a steady electric current resembles a magnetic dipole at distances large compared to the dimensions of the loop. | ||
The magnetic force between two charges moving in a medium of relative permeability ''μ<sub>r</sub>'' is provided by the [[Lorentz force]]. Let the charges be ''q<sub>1</sub>'', ''q<sub>2</sub>'', their separation be '''''r<sub>12</sub>''''', and their constant velocities be '''''v<sub>1</sub>''''', '''''v<sub>2</sub>'''''. Then the force | The magnetic force between two charges moving in a medium of relative permeability ''μ<sub>r</sub>'' is provided by the [[Lorentz force]] acting upon one charge ''via'' the magnetic flux density generated by the other as predicted by the [[Biot-Savart law]]. Let the charges be ''q<sub>1</sub>'', ''q<sub>2</sub>'', their separation be '''''r<sub>12</sub>''''', and their constant velocities be '''''v<sub>1</sub>''''', '''''v<sub>2</sub>'''''. The magnetic field generated by charge ''2'' at a position ''P'' is:<ref name=Tipler> | ||
{{cite book |pages=p. 884 |chapter=The magnetic field of moving point charges |url=http://books.google.com/books?id=Gp2tzUhbqjMC&pg=PA884 |author=Paul A. Tipler |isbn=9781572594920 |year=1998 |edition=4rth ed |publisher=W. H. Freeman |title=Physics for Scientists and Engineers, Parts 1-35; Part 39}} | |||
</ref> | |||
:<math>\mathbf B = \frac{\mu_r \mu_0}{4 \pi} \ \frac {q_2 \mathbf{v_2 \ \times \ \hat u }} {r^2} \ , </math> | |||
where '''''û''''' is a unit vector pointing from the charge to the field evaluation point ''P'', and ''r'' is the distance between the charge and the field point. | |||
Then the force upon charge ''1'' located at ''P<sub>1</sub>'' due to charge ''2'' according to the Lorentz law is:<ref name=Camara> | |||
{{cite book |title=Power Reference Manual for the Electrical and Computer PE Exam |author=John A. Camara |url=http://books.google.com/books?id=r_rDg_E97MEC&pg=SA16-PA15 |isbn=1591261627 |chapter=§22: Biot-Savart law |year=2010 |pages=p. 16-15 |publisher=Professional Publications, Inc.}} | {{cite book |title=Power Reference Manual for the Electrical and Computer PE Exam |author=John A. Camara |url=http://books.google.com/books?id=r_rDg_E97MEC&pg=SA16-PA15 |isbn=1591261627 |chapter=§22: Biot-Savart law |year=2010 |pages=p. 16-15 |publisher=Professional Publications, Inc.}} | ||
| Line 33: | Line 43: | ||
</ref> | </ref> | ||
:<math>\mathbf{F_{12}} = \frac{\mu_r \mu_0 }{4 \pi} | :<math>\mathbf{F_{12}} = q_1 \mathbf {v_1 \ \times \ B }(P_1)</math> | ||
:<math>= | |||
\frac{\mu_r \mu_0 }{4 \pi} | |||
\ | \ | ||
\frac {q_1 q_2}{r_{12}^2} | \frac {q_1 q_2}{r_{12}^2} | ||
\left( | \left( | ||
\mathbf{v_1 \ \times \ } | \mathbf{v_1 \ \times \ } | ||
(\mathbf{v_2 \ \times \ \hat{u}_{12}} ) | (\mathbf{v_2 \ \times \ \hat{u}_{12}} ) | ||
\right) \ , | \right) \ , | ||
</math> | </math> | ||
where '''''û<sub>12</sub>''''' is a unit vector pointing from charge ''2'' to charge ''1''. This relation is closely connected to the force between two current elements, as described by Grassmann's adaptation of [[Ampère's equation]], described next. | where '''''û<sub>12</sub>''''' is a unit vector pointing from charge ''2'' to charge ''1'' and ''r<sub>12</sub>'' is their separation. This relation is closely connected to the force between two current elements, as described by Grassmann's adaptation of [[Ampère's equation]], described next. | ||
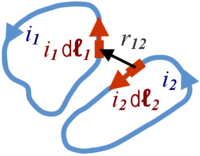
The force exerted between infinitesimal current elements from two loops carrying currents ''I<sub>i</sub>'' and ''I<sub>j</sub>'' and immersed in a magnetic medium with relative permeability ''μ<sub>r</sub>'' is changed by a factor ''μ<sub>r</sub>''. The infinitesimal current elements have vector components ''i<sub>i</sub>''d'''ℓ<sub>i</sub>''' and ''i<sub>j</sub>''d'''ℓ<sub>j</sub>''' where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Grassmann's law for the force upon current element ''i'' exerted by current element ''j'' is:<ref name=Assis> | The force exerted between infinitesimal current elements from two loops carrying currents ''I<sub>i</sub>'' and ''I<sub>j</sub>'' and immersed in a magnetic medium with relative permeability ''μ<sub>r</sub>'' is changed by a factor ''μ<sub>r</sub>''. The infinitesimal current elements have vector components ''i<sub>i</sub>''d'''ℓ<sub>i</sub>''' and ''i<sub>j</sub>''d'''ℓ<sub>j</sub>''' where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Grassmann's law for the force upon current element ''i'' exerted by current element ''j'' is:<ref name=Assis> | ||
Revision as of 08:34, 21 April 2011
In physics, in particular in magnetostatics, the relative permeability is an intrinsic property of a magnetic material. It is usually denoted by μr. For simple magnetic materials, using SI units, μr is related to the proportionality constant between the magnetic flux density B and the magnetic field H, namely B = μr μ0 H, where μ0 is the magnetic constant. The relative permeability describes the ease by which a magnetic medium may be magnetized.
A related quantity is the magnetic susceptibility, denoted by χm, related to the magnetic permeability in SI units by:[1]
The relative permittivity μr may be greater than or less than 1. For simple media, if μr < 1 (χm negative), the medium is termed diamagnetic; if μr > 1 (χm positive) paramagnetic. Only classical vacuum has μr = 1 (exact). A typical diamagnetic susceptibility is about −10−5, while a typical paramagnetic susceptibility is about 10−4.
Relation to forces
See also Ampère's equation.
Similar to Coulomb's law describing the electric force between electric charges, the magnetic force between two magnetic poles of pole strength given by p1 and p2 and separated by distance r in a medium of relative permeability μr has magnitude F:
and is directed along the line joining the poles. It is attractive if the poles are opposite in nature (one north pole and one south pole) and repulsive if they are the same.
It happens, however, that magnetic poles always occur as opposite pairs, so the force law between single poles cannot be observed directly. However, magnetic dipoles do occur in nature and can be directly observed. A planar wire loop conducting a steady electric current resembles a magnetic dipole at distances large compared to the dimensions of the loop.
The magnetic force between two charges moving in a medium of relative permeability μr is provided by the Lorentz force acting upon one charge via the magnetic flux density generated by the other as predicted by the Biot-Savart law. Let the charges be q1, q2, their separation be r12, and their constant velocities be v1, v2. The magnetic field generated by charge 2 at a position P is:[2]
where û is a unit vector pointing from the charge to the field evaluation point P, and r is the distance between the charge and the field point.
Then the force upon charge 1 located at P1 due to charge 2 according to the Lorentz law is:[3]
where û12 is a unit vector pointing from charge 2 to charge 1 and r12 is their separation. This relation is closely connected to the force between two current elements, as described by Grassmann's adaptation of Ampère's equation, described next.
The force exerted between infinitesimal current elements from two loops carrying currents Ii and Ij and immersed in a magnetic medium with relative permeability μr is changed by a factor μr. The infinitesimal current elements have vector components iidℓi and ijdℓj where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Grassmann's law for the force upon current element i exerted by current element j is:[4]
as is readily derived from the Biot-Savart law, and is consistent with space-time symmetry. Here ûij is a unit vector pointing from element j to element i along the line joining them, and rij the length of this line. The force element is second order because it is a product of two infinitesimals.
Background
Maxwell reduced electrodynamics to the knowledge of charge and current distributions, and introduced the notion of material properties (constitutive relations) relating magnetic flux density B to magnetic field H and electric displacement D to electric field E. In implementing these relations, it should be noted that the use of a constant as the relative permeability of a substance is an approximation, even for quantum vacuum. A more complete representation recognizes that all media exhibit departures from this approximation, in particular, a dependence on field strength, a dependence upon the rate of variation of the field in both time and space, and a dependence upon the direction of the field. In many materials these dependencies are slight; in others, like ferromagnets, they are pronounced.
Notes
- ↑ For example see Yehuda Benzion Band. Light and matter: electromagnetism, optics, spectroscopy and lasers. John Wiley and Sons, p. 242. ISBN 0471899313.
- ↑ Paul A. Tipler (1998). “The magnetic field of moving point charges”, Physics for Scientists and Engineers, Parts 1-35; Part 39, 4rth ed. W. H. Freeman, p. 884. ISBN 9781572594920.
- ↑ John A. Camara (2010). “§22: Biot-Savart law”, Power Reference Manual for the Electrical and Computer PE Exam. Professional Publications, Inc., p. 16-15. ISBN 1591261627.
- ↑ See for example, André KT Assis (1995). “Equation (9)”, Julian B. Barbour, Herbert Pfister, eds: Mach's principle: from Newton's bucket to quantum gravity. Birkhäuser Publishers, p. 162. ISBN 0817638237.