Tania function: Difference between revisions
imported>Dmitrii Kouznetsov (load the draft; still some incompatibilities...) |
imported>Dmitrii Kouznetsov (make up the formulas) |
||
| Line 1: | Line 1: | ||
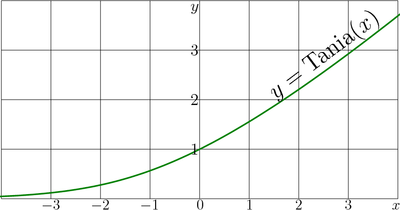
[[File:TaniaPlot.png|400px|right|thumb|<math>y=\mathrm{Tania}(x)</math>]] | [[File:TaniaPlot.png|400px|right|thumb|Explicit plot of <math>y=\mathrm{Tania}(x)</math>]] | ||
'''Tania function''' is solution <math>f\!=\!\mathrm{Tania}</math> of equation | '''Tania function''' is solution <math>f\!=\!\mathrm{Tania}</math> of equation | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (1) ~ ~ ~ f'(z)= \frac{f(z)}{1+f(z)} </math> | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (1) ~ ~ ~ f'(z)= \frac{f(z)}{1+f(z)} </math> | ||
| Line 13: | Line 13: | ||
<math>v\!=\!\Im(f)\!=\! \mathrm {const} ~</math>]] | <math>v\!=\!\Im(f)\!=\! \mathrm {const} ~</math>]] | ||
The inverse function of Tania can be called '''ArcTania'''; < | The inverse function of Tania can be called '''ArcTania'''; <math>\mathrm{ArcTania}=\mathrm{Tania}^{-1}</math>. The ArcTania is elementary function: | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (3) ~ ~ ~ | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (3) ~ ~ ~ | ||
\mathrm{ArcTania}(z)=z+\ln(z)-1</math> | \mathrm{ArcTania}(z)=z+\ln(z)-1</math> | ||
<!-- The expression (3) is valid for <math>z\in \mathbb C \backslash \{z\in \mathbb R, z\le 0 \}</math>, because of the !--> | <!-- The expression (3) is valid for <math>z\in \mathbb C \backslash \{z\in \mathbb R, z\le 0 \}</math>, because of the !--> | ||
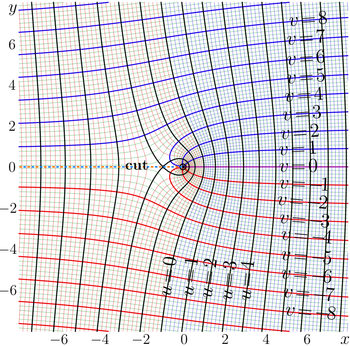
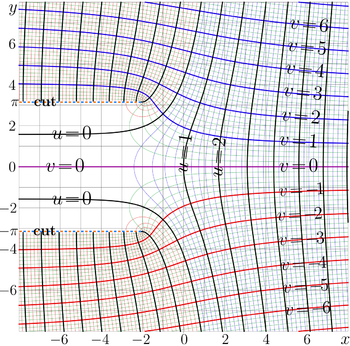
The [[Complex map]]s of <math>f\!=\!\mathrm{ArcTania}(z)</math> and <math>f\!=\!\mathrm{Tania}(z)</math> are shown in figures at right in the plane <math>x\!=\!Re(z)~,~ y\!=\!\Im(z)</math> | The [[Complex map]]s of <math>f\!=\!\mathrm{ArcTania}(z)</math> and <math>f\!=\!\mathrm{Tania}(z)</math> are shown in figures at right in the plane <math>x\!=\!\Re(z)~,~ y\!=\!\Im(z)</math> | ||
with | with | ||
lines <math>u\!=\!\Re(f)\!=\!\mathrm{const}</math> and | lines <math>u\!=\!\Re(f)\!=\!\mathrm{const}</math> and | ||
| Line 27: | Line 27: | ||
In certain range of values of the argument, the Tania function can be expressed through the [[LambertW function]] (known also as '''ProductLog function''') as follows: | In certain range of values of the argument, the Tania function can be expressed through the [[LambertW function]] (known also as '''ProductLog function''') as follows: | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (4) ~ ~ ~ | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (4) ~ ~ ~ | ||
\mathrm{Tania}(z)=\mathrm{LambertW}( | \mathrm{Tania}(z)=\mathrm{LambertW}(\exp(1\!+\!z)) | ||
~</math>, <math>~ ~ |\Im(z)|<\pi</math> | ~</math>, <math>~ ~ |\Im(z)|<\pi</math> | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (5) ~ ~ ~ | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (5) ~ ~ ~ | ||
\mathrm{LambertW}( | \mathrm{LambertW}(z)=\mathrm{Tania}\big(\ln(z) -1 \big) | ||
~</math> | ~</math> | ||
At least in facility of the real axis, the Tania function can be expressed through the LambertW function; | At least in facility of the real axis, the Tania function can be expressed through the LambertW function; | ||
| Line 99: | Line 99: | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \mathrm{Tania}(z)=</math> <math> (z\!+\!1)\!-\!\ln(z\!+\!1) | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \mathrm{Tania}(z)=</math> <math> (z\!+\!1)\!-\!\ln(z\!+\!1) | ||
+\frac{ \ln(z\!+\!1)}{z+1}</math> <math> | +\frac{ \ln(z\!+\!1)}{z+1}</math> <math> | ||
+\ | +\Big(\frac{ \ln(z\!+\!1)}{z+1}\Big)^{\!2} \Big(\frac{1}{2}-\ln(z\!+\!1)^{-1}\Big) | ||
+\ | +\Big(\frac{ \ln(z\!+\!1)}{z+1}\Big)^{\!3} \Big( | ||
\frac{1}{3}-\frac{3}{4} \ln(z\!+\!1)^{-1}+ \ln(z\!+\!1)^{-2}\ | \frac{1}{3}-\frac{3}{4} \ln(z\!+\!1)^{-1}+ \ln(z\!+\!1)^{-2}\Big)</math> <math> | ||
+\ | +\Big(\frac{ \ln(z\!+\!1)}{z+1}\Big)^{\!4} \Big( | ||
\frac{1}{4}-\frac{11}{\!5} \ln(z\!+\!1)^{-1}+3\ln(z\!+\!1)^{-2}-\ln(z\!+\!1)^{-3}\ | \frac{1}{4}-\frac{11}{\!5} \ln(z\!+\!1)^{-1}+3\ln(z\!+\!1)^{-2}-\ln(z\!+\!1)^{-3}\Big)</math> <math> | ||
+ O\Big( \frac{\ln(z\!+\!1)}{z+1}\Big)^{\!5} | + O\Big( \frac{\ln(z\!+\!1)}{z+1}\Big)^{\!5} | ||
</math> | </math> | ||
| Line 118: | Line 118: | ||
Such expansion can be obtained iterating assignment | Such expansion can be obtained iterating assignment | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (10) ~ ~ ~ | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (10) ~ ~ ~ f=\varepsilon \exp(-f)</math> | ||
with the initial approach </math>f=\varepsilon + O(\varepsilon^2)</math>. | with the initial approach </math>f=\varepsilon + O(\varepsilon^2)</math>. | ||
| Line 140: | Line 140: | ||
For the expansion of <math>\mathrm{Tania}(z)</math> at the upper branch point <math>z=-2+\pi \mathrm i</math>, the convenient small parameter is | For the expansion of <math>\mathrm{Tania}(z)</math> at the upper branch point <math>z=-2+\pi \mathrm i</math>, the convenient small parameter is | ||
: <math> \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! ( | : <math> \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (11) ~ ~ ~ | ||
t= \mathrm{i} \sqrt{ \frac{2}{9} (z+2-\pi \mathrm i )~} </math> | t= \mathrm{i} \sqrt{ \frac{2}{9} (z+2-\pi \mathrm i )~} </math> | ||
then, the expansion of Tania can be written as follows: | then, the expansion of Tania can be written as follows: | ||
: <math>\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! ( | : <math>\displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (12) ~ ~ ~ \mathrm{Tania}(z)=</math> <math> | ||
-1+3t-3t^2</math> <math> | -1+3t-3t^2</math> <math> | ||
+\frac{3}{4} t^3</math> <math> | +\frac{3}{4} t^3</math> <math> | ||
| Line 168: | Line 168: | ||
The [[Taylor expansion]] of Tania at zero | The [[Taylor expansion]] of Tania at zero | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle ( | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (13) ~ ~ ~ \mathrm{Tania}(z)=</math> <math>1 </math> <math> | ||
+\frac{z}{2}</math> <math> | +\frac{z}{2}</math> <math> | ||
+\frac{z^2}{16}</math> <math> | +\frac{z^2}{16}</math> <math> | ||
| Line 179: | Line 179: | ||
</math> | </math> | ||
converges at <math>|z|<\sqrt{4+\pi^2}\approx 3.724</math>; this series can be obtained with the [[Mathematica]]'s operator [[InverseSeries]], converting the expansion | converges at <math>|z|<\sqrt{4+\pi^2}\approx 3.724</math>; this series can be obtained with the [[Mathematica]]'s operator [[InverseSeries]], converting the expansion | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle ( | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (14) ~ ~ ~ \mathrm{ArcTania}(z)=</math> <math> | ||
2(z\!-\!1)</math> <math> | 2(z\!-\!1)</math> <math> | ||
-\frac{(z\!-\!1)^2}{2}</math> <math> | -\frac{(z\!-\!1)^2}{2}</math> <math> | ||
| Line 187: | Line 187: | ||
+\frac{(z\!-\!1)^6}{6}</math> <math> | +\frac{(z\!-\!1)^6}{6}</math> <math> | ||
+~ {O}(z\!-\!1)^7</math> | +~ {O}(z\!-\!1)^7</math> | ||
However, more terms can be added to the series in ( | However, more terms can be added to the series in (13) and (14). At moderate values of <math>|z|\lesssim 1</math>, | ||
the exansion (11) can be used for the efficient (quick and precise) evaluation of <math>\mathrm{Tania}(z)</math>; | the exansion (11) can be used for the efficient (quick and precise) evaluation of <math>\mathrm{Tania}(z)</math>; | ||
in order to get 14 significant decimal digits, it is sufficient to take 20 terms. | in order to get 14 significant decimal digits, it is sufficient to take 20 terms. | ||
In the similar way, the expansion of <math>\mathrm{Tania}(z)</math> at <math>z=-2+1/\mathrm e\approx -1.632</math> can be written as follows: | In the similar way, the expansion of <math>\mathrm{Tania}(z)</math> at <math>z=-2+1/\mathrm e\approx -1.632</math> can be written as follows: | ||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle ( | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle (15) ~ ~ ~ \mathrm{Tania}(z)=</math> <math> | ||
\frac{1}{\mathrm{e}} </math> <math> | \frac{1}{\mathrm{e}} </math> <math> | ||
+ \frac | + \frac | ||
| Line 207: | Line 207: | ||
The series above can be used for the evaluation of <math>\mathrm{Tania}(z)</math>, dependently on value of <math>z</math>. | The series above can be used for the evaluation of <math>\mathrm{Tania}(z)</math>, dependently on value of <math>z</math>. | ||
The increase of the precision of the evaluation is easier to achieve not with the increase of number of terms in the expansion, but applying the Newton method. Let <math>s_0</math> be initial approximation, obtained with the appropriate formulas from the set above; let | The increase of the precision of the evaluation is easier to achieve not with the increase of number of terms in the expansion, but applying the Newton method. Let <math>s_0</math> be initial approximation, obtained with the appropriate formulas from the set above; let | ||
: <math> \displaystyle \!\!\!\!\!\!\!\!\!\! ( | : <math> \displaystyle \!\!\!\!\!\!\!\!\!\! (16) ~ ~ ~ s_{n+1}=s_n + \frac{z-\mathrm{ArcTania}(s_n)}{\mathrm{ArcTania}'(s_n)}</math> | ||
where | where | ||
: <math> \displaystyle \!\!\!\!\!\!\!\!\!\! ( | : <math> \displaystyle \!\!\!\!\!\!\!\!\!\! (17) ~ ~ ~\mathrm{ArcTania}'(z)=1+1/z</math> | ||
is derivative of the ArcTania function by equation (3). | is derivative of the ArcTania function by equation (3). | ||
The primary approximations considered in the previous sections allow to get good initial approximation for any point of the complex plane; | The primary approximations considered in the previous sections allow to get good initial approximation for any point of the complex plane; | ||
Revision as of 07:40, 25 September 2011
Tania function is solution of equation
with initial condition
Relation with other special functions
The inverse function of Tania can be called ArcTania; . The ArcTania is elementary function:
The Complex maps of and are shown in figures at right in the plane with lines and lines .
At least for , the relation below holds
In certain range of values of the argument, the Tania function can be expressed through the LambertW function (known also as ProductLog function) as follows:
- ,
At least in facility of the real axis, the Tania function can be expressed through the LambertW function; while the principal branch of the LabdaW function can be expressed through the Tania function for all complex values of the argument.
History
The Tania function is used in the Laser science for the description of intensity of light in the idealized gain medium.
The Tania function appears as the intensity of a wave in the infirmly pumped gain medium, measured in unit of the saturation intensity. Then, its argument has sense of length of propagation, measured in units of the inverse of unsaturated gain. Such a model describes the idealized laser amplifier with simple kinetics, and can be applied, for example, to the Yb-doped ceramics pumped in vicinity of wavelength of order of 940nm; the maximum gain corresponds to wavelength in vicinity of 1030 nm. For this wavelength, the saturation intensity may have value of order of </math>I_{\rm sat}=100 {\rm W/mm}^2</math>, and the unsaturated gain (that depends on the concentration of dopant and the intensity of pump) may be of order of </math>g_0 \approx 1/\mathrm{mm}</math> [1]. This determines the orders of magnitude of values of the physical parameters, while the intensity along the propagation at distance </math>x</math> can be described with intensity satisfying the equation
The solution </math>I</math> can be expressed as
where is distance at which the intensity saturates the gain, id est, .
The phenomenology of waves with such a saturated gain has been considered in century 20; some results are published in the Soviet Journal of Quantum Electronics [2][3]. The function "Tania" is named after the short name of the first author of [3].
For the applications, the simple and robust implementation of the Tania function is an important tools of the scientific research. For this reason, the description of the Tania function is loaded at TORI (Tools for Outstanding Research and Investigations) [4]. Some part of that article is reproduced below.
Properties of Tania and ArcTania
The complex map of the Tania function is shown in the figure at right.
in the </math>x,y</math> plane is shown with levels
and
.
The has two cut lines, , . In the figure, these lines are marked with dashed half-lines. The branch points are determined by the singularity of the expression in the right hand side of equation (1), they correspond to values of ArcTania at </math>-. Using (3), these points can be expressed as follows:
- .
In the left hand side of the figure, between the cut lines lines, the function exponentially approaches zero. In other directions, the modulus of the function is smoothly growing; the growth is similar to that of the linear function.
Tania is real–holomorhic;
The expansions of Tania in diffrent cases, and, in particular, at the branchpoints </math>z_\pm</math> is described below.
Expansion of Tania at infinity
The complex maps of Tania and ArcTania above show that asymptotically each of these functions becomes similar to its argument. Being far from the branch points (and outside the cut lines), the grid of the lines of constant real and constant imaginary part looks similar to that of the identity function. This indicates that the leading term of the expansion at infinity of </math>\mathrm{Tania}(z)</math> should be just </math>z</math>. Such an expansion is suggested in this section.
At large values of the argument, Tania shows almost linear growth and can be expanded as follows:
At , the truncated series (7) can be used for the evaluation of </math>\mathrm{Tania}(z)</math>, while the argument is not between the cut lines in figure. For the evaluation, the asymptotic can be written also as follows:
Asymptotic expansion of Tania between the cut lines
The expansions (7) and (8) are not valid between the cut lines. For this range, for large values of the argument, the special expansion is suggested in this section.
For at
where .
Such expansion can be obtained iterating assignment
with the initial approach </math>f=\varepsilon + O(\varepsilon^2)</math>.
The example of the truncated series is shown in figure at right. The same notations for the complex map are used. In the shaded region, the precision is less than 3. In particular, the expansion (8) does not approximate </math>\mathrm{Tania}(z)</math> at </math>\Re(z)\!>\!-2~</math>. However, the truncated series can be used for the precise evaluation of </math>\mathrm{Tania}(z)</math> at , .
Together with the expansion (8), the expansion (9) covers the most of the complex plane, leaving only a finite-size domain that includes the branch points and the origin of the coordinates. The expansion at these points are considered below.
Expansion of Tania at singularities
has two cut lines at </math>\Re(z)\!\le\! -2</math>, . The expansions above do not reproduce the behavior of Tania in vicinity of the branch points. In this section, the expansion at these branch points is suggested.
For the expansion of at the upper branch point , the convenient small parameter is
then, the expansion of Tania can be written as follows:
The Mathematica Series routine easy calculates some tens of the first coefficients of the expansion. The series seems to converge while ; in vicinity of another branch point, id est, at , such an approximation is not valid.
The figure at right shows complex map of the truncated series by (10) in the same notations as in the previous maps. The shaded region indicate the domain where the precision of the approximation is less than 3; in the white spot the the approximation by the polynomial of 5th order with respect to gives at least three significant figures.
In vicinity of the origen of coordinates, for example, at , the truncated series (with term of order of and higher dropped) provides of order of 2 decimal digits, and the deviation of line from the abscissa axis is barely seen in the figure.
Similar expansion of Tania at point can be obtained by complex conjugation of expressions (9) and (10).
Taylor expansions of Tania
The expansions above, in principle, allow to cover all the complex plane with the approximations of the Tania function. But the expansion at the branch points may be not convenient while dealing with Tania of a real argument. For this case, the Taylor expansions of Tania at the real axis are suggested in this section.
The Taylor expansion of Tania at zero
converges at ; this series can be obtained with the Mathematica's operator InverseSeries, converting the expansion
However, more terms can be added to the series in (13) and (14). At moderate values of , the exansion (11) can be used for the efficient (quick and precise) evaluation of ; in order to get 14 significant decimal digits, it is sufficient to take 20 terms.
In the similar way, the expansion of at can be written as follows:
The series converges at </math>\big|z+2-\frac{1}{\mathrm{e}}\big|</math> .
The truncated expansions above cover all the complex plane with at least 3–digit approximations.
Evaluation of Tania function
The series above can be used for the evaluation of , dependently on value of . The increase of the precision of the evaluation is easier to achieve not with the increase of number of terms in the expansion, but applying the Newton method. Let be initial approximation, obtained with the appropriate formulas from the set above; let
where
is derivative of the ArcTania function by equation (3). The primary approximations considered in the previous sections allow to get good initial approximation for any point of the complex plane; then the sequence converges to .
The sequence converges faster than exponentially. Practically, of order of 5 terms in some of the primary approximations are sufficient, and then the third iteration approximates with 15 decimal digits. Working with the complex(double( variables, there is no way to make the precision better. In such a way, the Tania function is represented in the C++ implementation used to plot the figures. Few tens operations are sufficient to get the maximal precision available; so, all the graphics can be plotted in the real time with the generators supplied. (Click the figure to see the implementation.)
Conclusions
The Tania function came from the Laser science describing evolution of the light intensity in the gain medium with simple kinetics. The inverse of Tania function is elementary function.
The C++ complex(double) implementation is used for generators of the figures.
The LambertW function (known also as ProductLog function) can be expressed through the Tania function.
References
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2005josab.pdf D.Kouznetsov, J.-F.Bisson, K.Takaichi, K.Ueda. High-power single mode solid state laser with short unstable cavity. -- JOSA B, v.22, Issue 8, p.1605-1619 (2005).
- ↑ http://tori.ils.uec.ac.jp/PAPERS/kk01.pdf T.I.Kuznetsova, D.Yu.Kuznetsov. Interaction of a spatially-modulated wave of complex structure and a plane wave in a quantum amplifier. Soviet J. of Quantum Electronics, 1981, v.11, N.8, p.1090-1094.
- ↑ 3.0 3.1 http://www.ils.uec.ac.jp/%7Edima/PAPERS/ke14-1471.pdf T.I.Kuznetsova, D.Yu.Kuznetsov. Interaction between counterrunning spatially modulated beams in a non-linear medium. Soviet J. of Quantum Electronics, 1984, v.14, N.11, p.1471-1474.
Cite error: Invalid
<ref>tag; name "kk" defined multiple times with different content - ↑ http://tori.ils.uec.ac.jp/TORI/index.php/Tania_function