Natural pentation: Difference between revisions
imported>Dmitrii Kouznetsov mNo edit summary |
imported>Dmitrii Kouznetsov m (misprint) |
||
| Line 1: | Line 1: | ||
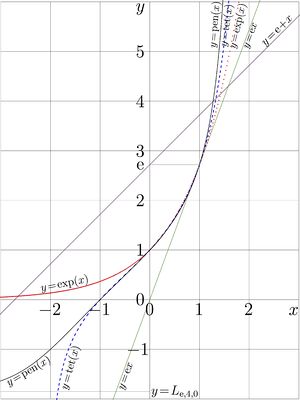
[[File:Ackerplot400.jpg|300px|thumb| [[Natural pentation]] compared to other [[ackermanns]] ]] | [[File:Ackerplot400.jpg|300px|thumb| [[Natural pentation]] compared to other [[ackermanns]] ]] | ||
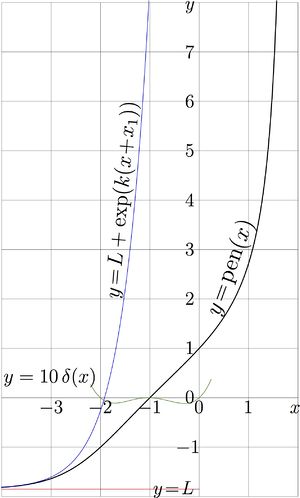
[[File:Penplot.jpg|300px|thumb|<math>y\!=\!\mathrm{pen}(x)</math> and its approximations]] | [[File:Penplot.jpg|300px|thumb|<math>y\!=\!\mathrm{pen}(x)</math> and its approximations]] | ||
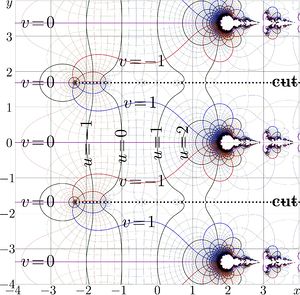
[[File:Penmap.jpg|300px|thumb| <math>u\!+\!\mathrm i v=\mathrm{pen}(x\!+\!\mathrm i y)</math> in the < | [[File:Penmap.jpg|300px|thumb| <math>u\!+\!\mathrm i v=\mathrm{pen}(x\!+\!\mathrm i y)</math> in the <math>x,y</math> plane]] | ||
Pentation appears as 5th [[ackermann]]. | Pentation appears as 5th [[ackermann]]. | ||
Revision as of 00:20, 9 September 2014
Pentation appears as 5th ackermann.
For , Pentation specific superfunction of tetration , constructed with regular iteration at its lowest real fixed point. Pentation is denoted with symbol pen;
where is Fifth ackermann to base . [1][2].
If the base of tetration , then the tetration is called natural tetration and the corresponding pentation is called Natural pentation. Namely this case is considered on this article.
The first 5 ackermanns (addition of e, multiplication by e, exponent, tetration, pentation) are shown in the top figure at right.
Natural pentation is compared to its asymptotics at the second figure.
The complex map of the natural pentation is shown in the last figure.
General properties
Pentation satisfies the transfer equation
where is tetration to base . The additional condition, common for all ackermanns is assumed,
Pentation is holomorphic at least in the part of the complex plane, while the real part of the argument does not exceed some constant. For , this constant is about
The range of holomorphism of pentation includes alto the real axis.
For the real base </math>b>1</math>, pentation is real–holomorphic,
Pentation has the exponential asymptotic at large negative values of the real part of the argument,
where is fixed point of tetration, it is solution of equation
,
parameters and depend on the base </math>b</math>. For base , the increment </math>k</math> is positive. This increment is determined by the derivative of tetration at its lowest real fixed point, and pentation is periodic function; the period </math>P=2 \pi \mathrm i /k</math>. For real base , the increment is positive.
Properties of the natural pentation
The base of pentation is indicated as subscript, but it it is e, the subsctipt can be omitted, as in the case of tetration, arctetration, exponential and logarithm. The natural pentation is superfunction of natural tetration tet [3][4].
Natural pentation has the following properties:
The limiting value at minus infinity is fuxed point of the natural tetration,
Increment at negative values of the real part is
Period
The period is pure imaginary, so, the map shown in the figure reproduces at the translations along the imaginary axis. A little bit more than two periods are covered by the range of the complex map at right.
Natural pentation has the countable set of logarithmic singularities. The cut lines divide the right hand side of the complex plane to the set of "independent" strips of width . In addition, there are many branch points at the right hand side of the map in vicinity of the real axis; and these branch points also reproduce at the translations for period . There is no way to direct these cut lines to the left, because infinite amount of singularities are in the right hand side of the complex map.
Along the real axis, at minus infinity, the function pen grows exponentially from its asymptotic value
The graphic passes through points with coordinates , , , .
In vicinity of the range , natural pentation can be approximated with linear function, ; this approximation gives of order of 2 correct decimal digits. Error of this approximation can be characterised with function . In order to make it visible, it is scaled with factor 10, id est, curve is plotted with thin curve in the intermediate figure.
At larger positive values of the argument, pentation shows very fast growth, much faster than that of superfactorial or that of natural tetration.
Visually, looks as infinity, and, perhaps, can be considered a "numerical approximation" of the fake Mizugadro number. Tetration has singularity and the branch point , and this singularity determines the set of singularities in vicinity of the real axis. The pair of these singularities are seen at points with coordinates approximately ; the zooming of the map allows to see them in details.
Construction and evaluation of tetration, pentation and highest ackermanns may be good excersice for testing and debugging of the automatic procedure for calculation of superfuncions and non-integer iterates of holomorphic functions. Up to year 2014, such an automatic procedure is not yet implemented, and the superfunctions are built-up semi-manually; with human control of the overlapping of various representations and manual check of the residual at the substitution of various approximations into the transfer equation. [1][5]
References
- ↑ 1.0 1.1 https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014, in Russian.
- ↑
http://www.ils.uec.ac.jp/~dima/PAPERS/2014acker.pdf
http://mizugadro.mydns.jp/PAPERS/2014acker.pdf D.Kouznetsov. Holomorphic ackermanns. 2014, under consideration. - ↑
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. - ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑
http://www.ils.uec.ac.jp/~dima/PAPERS/2014acker.pdf
http://mizugadro.mydns.jp/PAPERS/2014acker.pdf D.Kouznetsov. Holomorphic ackermanns. 2014, under consideration.
The first version of this article is adopted from TORI, http://mizugadro.mydns.jp/t/index.php/Pentation
Keywords
Ackermann, Pentation, Superfunction, Tetration, Transfer equation