Newton's method
Newton's method, also called the Newton-Raphson method or Newton iteration, is a root-finding algorithm; that is, a method for finding where a function obtains the value zero.
Description
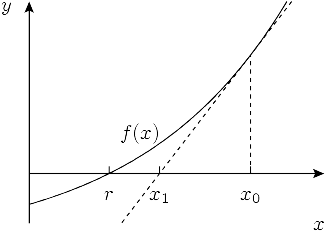
Newton's method is based on the insight that any smooth function f can be approximated locally by its tangent. If r is a root of f, the tangent of f at any point close to r is a good approximation of f, and hence the point where the tangent intercepts the x-axis is a good approximation of r. This suggests that if we know an approximation xk for r, we obtain an even better approximation xk+1 from the root of the tangent line that goes through (x, f(x)). Expressing the equation for the tangent in the terms of , the derivative of f, gives the solution
The calculation of an improved approximation with this formula is called a Newton step or Newton update. Newton's method consists of repeating this step for k = 0, 1, 2, ... to obtain successively better estimates x1, x2, x3, ... for r. Provided that the initial guess x0 is sufficiently close to r and that f is sufficiently well-behaved, the estimates will converge rapidly to r as k goes to infinity.
Example: calculating the golden ratio
The golden ratio (φ ≈ 1.618) is the largest root of the polynomial . To calculate this root, we can use the Newton iteration
with the initial estimate x0 = 1. Using double-precision floating-point arithmetic, which allows a precision of roughly 16 digits, we obtain the following approximations:
- x0 = 1.0
- x1 = 2.0
- x2 = 1.6666666666666667
- x3 = 1.6190476190476191
- x4 = 1.6180344478216817
- x5 = 1.618033988749989
- x6 = 1.6180339887498947
- x7 = 1.6180339887498949
- x8 = 1.6180339887498949
Since the last update does not change the value, we can be reasonably sure to have obtained a value for the golden ratio that is correct to the available precision. It can be seen that each iteration roughly doubles the number of correct digits. We say that the rate of convergence is quadratic. Newton's method typically — but not always — achieves such fast convergence.
Convergence analysis
Suppose we have a function f with f(r) = 0. To analyze the convergence properties of Newton's method, we can use the Taylor series of f around xk. This gives
where . Assuming , dividing through gives
Moving terms to the left hand side and substituting the Newton update expression for xk+1 then gives
and a final division shows that
Hence, the rate of convergence is at least quadratic. However, if , meaning that f has a double root, it can be shown that the convergence is only linear.
- More detail needed
Examples of non-quadratic convergence
- Insert some example of linear convergence and/or convergence failure here
In rare cases, Newton's method may converge faster than quadratically. One such situation appears if we attempt to calculate π as the smallest positive number x for which sin x = 0. This equation leads to the Newton iteration
Knowing that π is a little larger than 3, we may start with the initial value x0 = 3. Three iterations give a value of π that is correct to full double precision:
- x0 = 3.0
- x1 = 3.1425465430742778
- x2 = 3.141592653300477
- x3 = 3.1415926535897931
In this case, the convergence is cubic; that is, every iteration roughly triples the number of correct digits.
It is important to note that the choice of initial value determined the outcome of this calculation. If we had started with a number too close to 0, the iteration would have converged to 0. More generally, if we had started with an approximation close to nπ for some integer n other than n = 1, the iteration would have converged to nπ. If we had started with a value x0 close to (n + 1/2)π, tan x0 would have been a very large number and x1 would have turned out far away from the origin.
Complex functions
Leads to Newton fractals
Newton's method as an optimization algorithm
Instead iterate
Multidimensional version
Gauss-Newton's method
Variations and practical implementation concerns
Damped, bracketed and hybrid methods
The fact that Newton's method may converge slowly or fail to converge for functions with horizontal tangents, or when given poor initial estimates, makes it unsuitable in raw form as a general-purpose root-finding algorithm. It is therefore typically combined with some mechanism for detecting and correcting convergence failure.
- Bracketed, hybrid
Newton's method can be combined with a slower but safer algorithm, such as the bisection algorithm.
limit number of iterations
- Damped
Quasi-Newton methods
Newton's method requires that the derivative of the object function be known, but in some situations the derivative or Jacobian may be unavailable or prohibitively expensive to calculate. The cost can be higher still when Newton's method is used as an optimization algorithm, in which case the second derivative or Hessian is also needed.
An alternative in these situations is to use an approximation of the derivative or second-derivative, which leads to so-called quasi-Newton methods. The most common strategy is to use the function values from two successive iterations to calculate a finite difference approximation for the derivative. This is equivalent to the secant method and reduces the rate of convergence from 2 to 1.618 (more precisely, the golden ratio). An alternative is to compute a value for the derivative or second derivative accurately, but reusing the same value for several successive iterations.
Modifications of Newton's method can also lead to more specialized algorithms, such as the Durand-Kerner method which is used to find simultaneous roots of a polynomial.
Computational complexity of inversion
Using Newton's method as described above, the time complexity of finding a simple root of a function f with n-digit precision is where F is the cost of calculating with n-digit precision. If f can be evaluated with variable precision, the algorithm can be improved. Because of the "self-correcting" nature of Newton's method, it is only necessary to use m-digit precision at a step where the approximation has m-digit accuracy. Hence, the first iteration can be performed with a precision twice as high as the accuracy of x0, the second iteration with a precision four times as high, and so on. If the precision levels are chosen suitably, only the final iteration requires f and its derivative to be evaluated at full n-digit precision. Provided that F grows superlinearly, which is the case in practice, the cost of finding a root is thus only .
Root-finding is essentially the same thing as calculating an inverse function. Hence, due to the aforementioned result, two differentiable functions that are inverse functions of each other have equivalent computational complexity and can be calculated in terms of each other in practice using Newton's method. In particular, it can be shown that:
- The exponential function, the natural logarithm, the trigonometric functions, and the inverse trigonometric functions, are all equivalent
- The algebraic operations of multiplication, division, and square root extraction are equivalent
During the second half of the 20th century, very efficient algorithms were found for multiplying large numbers and calculating high-precision natural logarithms with the aid of computers. Combined with Newton's method, all of the functions listed above can be calculated with this efficiency.
References
- Michael T. Heath (2002), Scientific Computing: An Introductory Survey, Second Edition, McGraw-Hill
- Jonathan M. Borwein & Peter B. Borwein (1987), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley Interscience





![{\displaystyle \xi _{k}\in [r,x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5b4541fd20e7a356be47b342c4adf48e89b4100)









