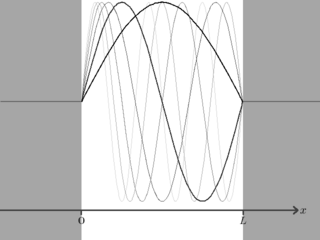
Particle in a box
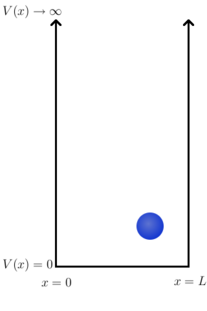
The particle in a box or infinite square well problem is one of the simplest non-trivial solutions to Schrödinger's wave equation. As such it is often encountered in introductory quantum mechanics material as a demonstration of the quantization of energy. In its simplest form the problem is one-dimensional, and involves a single particle living in an infinite potential well. What this means in the 1D case, which we examine here, is that there is a particle that is free to move back and forth along a line in between two points (e.g. 0 and , or and ). The particle is however constrained to this region, and cannot under any circumstances be found outside of it.
In this article we will rigorously define this problem and find the solutions to the corresponding Schrödinger wave equation, and then examine some of the properties and implications of these solutions.
The 1D square well
Setting up the problem
As depicted in Figure 1, the potential can be given by
- for and otherwise.
That is, in a region of length (the box or well) the potential is zero; everywhere else it is infinite. An immediate consequence of this is that the particle must be located somewhere between and , since if it were anywhere else it would have to have infinite energy.
This means that we only have to solve Schrödinger's equation inside the box and since the potential does not depend on time we can use the time-independent version of the Schrödinger equation. With in the box we have
where is Planck's constant divided by 2π, and and are the mass and energy of the particle, respectively. This is nothing but the eigenvalue problem, and our task is to determine the energy eigenvalue(s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} and eigenstate(s) that solve it. The equation is a second-order linear ODE with constant coefficients, and the general solution can be written as
where and are complex constants to be determined from conditions on the system. The first condition we can use is that the wavefunction must be continuous. We know that the particle cannot exist at positions , which tells us that the wavefunction must be identically zero there (in order for the probability of finding the particle there to also be zero). Continuity then implies that at the wavefunction is also zero, so we have
meaning that the wavefunction can now be written
Energy quantization
Using the same continuity argument at tells us that
One solution to this is of course . However, this would mean that the wavefunction vanishes everywhere -- implying that there is no particle! The other way to satisfy this equality is to have the sine term vanish, which will happen if
where mathematically can be any integer. This problem is not purely mathematical though, and we know for physical reasons that , , , and are all greater than zero. This means that must also be greater than zero, so is restricted to being a natural number, . We can now solve for the particle's energy,
where we have labelled the energy by the integer . We have just derived energy quantization! Without the potential well, i.e. if the particle was free, its energy would be allowed to take on any real number. Once inside the box though, only a specific discrete set of energy eigenvalues is permitted.
Substituting back into , we now have an infinite number of possible wavefunctions for the particle,
The final step is to determine the value of . This requires another condition that we can impose upon the problem.
Normalization
The probability of finding the particle somewhere must be . Since the wavefunction vanishes everywhere outside , the normalization condition is
Solving for tells us , where is some overall quantum phase (a real number). Because overall phases do not affect measurable results we are free to choose any value we want for without affecting the physics. For simplicity then, we set .
The solutions
We have now solved the particle-in-a-box problem. According to the Schrödinger wave equation the particle confined to the (infinite) box can only take on certain energy eigenvalues, namely
and the wavefunction for the particle when it is in the th energy eigenstate is
inside the box, and outside it.
Alternate description
Another common (equivalent) way to describe this problem is to shift the location of the box, so that it runs from to instead of to . The derivation of the allowed wavefunctions is very similar to what we did here, or the results can be obtained via coordinate transformation (specifically, a translation). With this different description of the square well the energy eigenvalues remain unchanged (as is to be expected[1]) while the resulting wavefunctions are given by[2]
if is odd, and
if is even.
Properties of the particle in a box
Completeness
The are complete, so form a basis for the possible wavefunctions, or states, of the particle. This means that an arbitrary state, , can be expressed as
where is the probability of measuring the particle's energy to be , and therefore finding the particle in state .
Non-vanishing ground state energy
The particle is not allowed to have zero energy, because if then , which makes the wavefunction
But if for all then there is zero probability of finding the particle no matter where you look -- which means that there is no particle! What this implies then is that the lowest allowed energy or ground state energy for the particle in the box is
The free space limit
We can think of 'free space' as an infinitely wide box. Therefore if we take , the width of the box, to infinity we would expect to find that in the limit we recover the result of a free particle. In fact, this is exactly what happens.
Mathematically we would find the same result for either of the solutions above, but physically free space doesn't have an infinite potential wall at . It is therefore more intuitive to look at the second solution, in which the potential well extends from to .
Notice that the energy spacing between two consecutive energy levels is
It is easy to see that for any finite value of the value of goes to zero as goes to infinity. This tells us that a free particle can have any (real, positive) energy.
Perhaps surprisingly the wavefunction also appears to go to zero everywhere in the limit, which at first may appear to be a problem. As discussed above if the wavefunction vanishes everywhere then there shouldn't be a particle. The difference in this case is subtle, and has to do with the fact that we are dealing with infinities. The important point to note is that if the particle is in state then the probability to find it if we look in the entire box is given by
which is independent of . This means that we would still find the particle if we looked in all of space after taking the limit
Generalization to 3D (to be done)
Spherical well
Cubic well
References
- ↑ The energy of a particle should not depend in any way on our choice of coordinate system, i.e. where we choose to place the origin .
- ↑ A. Messiah (1999) Quantum Mechanics: Two volumes bound as one ISBN 0486409244






























![{\displaystyle [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53e3bfad6c2b8297e8c8d2e84ce8f869d69b0d86)