Electron orbital

In quantum chemistry, an electron orbital (or more often just orbital) is a synonym for a quadratically integrable one-electron wave function. Here "orbital" is used as a noun. In quantum mechanics, the adjective orbital is often used as a synonym of "spatial", in contradistinction to spin.

Definitions of orbitals

Several kinds of orbitals can be distinguished.

Atomic orbital

The basic kind of orbital is the atomic orbital (AO). This is a function depending on a single 3-dimensional vector r_A1, which is a vector pointing from point A to electron 1. Generally there is a nucleus at A. The following notation for an AO is frequently used,

$\chi _{i}(\mathbf {r} _{A1}),$

but other notations can be found in the literature. Sometimes the center A is added as an index: χ_{A i}. We say that χ_{A i} (or, as the case may be, χ _i) is centered at A. In numerical computations AOs are either taken as Slater type orbitals (STOs) or Gaussian type orbitals (GTOs). Hydrogen-like orbitals are rarely applied in numerical calculations, but form the basis of many qualitative arguments in chemical bonding and atomic spectroscopy.

The orbital is quadratically integrable, which means that the following integral is finite,

$0\leq \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\chi _{i}(\mathbf {r} _{A1})^{*}\chi _{i}(\mathbf {r} _{A1})\;dx_{A1}\,dy_{A1}\,dz_{A1}\ <\infty .$

Its integrand being real and non-negative, the integral is real and non-negative. The integral is zero if and only if χ _i is the zero function.

Molecular orbital

The second kind of orbital is the molecular orbital (MO). Such a one-electron function depends on several vectors: r_A1, r_B1, r_C1, ... where A, B, C, ... are different points in space (usually nuclear positions). The oldest example of an MO (without use of the name MO yet) is in the work of Burrau (1927) on the single-electron ion H₂⁺. Burrau applied spheroidal coordinates (a bipolar coordinate system) to describe the wavefunctions of the electron of H₂⁺.

Lennard-Jones introduced the following linear combination of atomic orbitals (LCAO) way of writing an MO φ:

$\phi (\mathbf {r} _{1})=\sum _{A=1}^{N_{\mathrm {nuc} }}\sum _{i=1}^{n_{A}}c_{iA}\chi _{i}(\mathbf {r} _{A1}),\qquad c_{iA}\in \mathbb {C} ,$

where A runs over N_nuc different points in space (usually A runs over all the nuclei of a molecule, hence the name molecular orbital), and i runs over the n_A different AOs centered at A. The complex coefficients c _iA can be calculated by any of the existing effective-one-electron quantum chemical methods. Examples of such methods are the Hückel method and the Hartree-Fock method.

Spinorbitals

The AOs and MOs defined so far depend only on the spatial coordinate vector r_A1 of electron 1. In addition, an electron has a spin coordinate μ, which can have two values: spin-up or spin-down. A complete set of functions of μ consists of two functions only, traditionally these are denoted by α(μ) and β(μ). These functions are eigenfunctions of the z-component s_z of the spin angular momentum operator with eigenvalues ±½.

Spin atomic orbital

The most general spin atomic orbital of electron 1 is of the form

$\chi _{i}^{+}(\mathbf {r} _{A1})\alpha (\mu _{1})+\chi _{i}^{-}(\mathbf {r} _{A1})\beta (\mu _{1})$

which in general is not an eigenfunction of s_z. More common is the use of either

$\chi _{i}(\mathbf {r} _{A1})\alpha (\mu _{1})\quad {\hbox{or}}\quad \chi _{i}(\mathbf {r} _{A1})\beta (\mu _{1}),$

which are eigenfunctions of s_z. Since it is rare that different AOs are used for spin-up and spin-down electrons, we dropped the superscripts + and −.

Spin molecular orbital

A spin molecular orbital is usually either

$\phi ^{+}(\mathbf {r} _{1})\alpha (\mu _{1})\quad {\hbox{or}}\quad \phi ^{-}(\mathbf {r} _{1})\beta (\mu _{1}).$

Here the superscripts + and − might be necessary, because some quantum chemical methods distinguish the spatial wave functions of electrons with different spins. These are the so-called different orbitals for different spins (DODS) (or spin-unrestricted) methods. However, many quantum chemical methods apply the spin-restriction:

$\phi ^{+}(\mathbf {r} _{1})=\phi ^{-}(\mathbf {r} _{1})=\phi (\mathbf {r} _{1}).$

Chemists express this spin-restriction by stating that two electrons [electron 1 with spin up (α), and electron 2 with spin down (β)] are placed in the same spatial orbital φ. This means that the total N-electron wave function contains a factor of the type φ(r₁)α(μ₁)φ(r₂)β(μ₂).

History of term

Orbit is an old noun (1548), initially indicating the path of the Moon and later the paths of other heavenly bodies as well. The adjective "orbital" had (and still has) the meaning "relating to an orbit". When Ernest Rutherford in 1911 postulated his planetary model of the atom (the nucleus as the Sun, and the electrons as the planets) it was natural to call the paths of the electrons "orbits". Bohr, although he was the first to recognize (1913) orbits as stationary states of the hydrogen atom, used the word as well. However, after Schrödinger (1926) had solved his wave equation for the hydrogen atom (see this article for details), it became clear that the electronic "orbits" did not resemble planetary orbits at all. The wave functions of the hydrogen electron are time-independent and smeared out. They are more like unmoving clouds than like planetary orbits. As a matter of fact, the angular parts of the hydrogen wave functions are spherical harmonics and hence they have the same appearance as spherical harmonics. (See spherical harmonics for a few graphical illustrations).

In the 1920s electron spin was discovered, whereupon the adjective "orbital" started to be used in the meaning of "non-spin", that is, as a synonym of "spatial". In scientific papers of around 1930 one finds discussions about "orbital degeneracy", meaning that the spatial (non-spin) parts of several one-electron wave functions have the same energy. Also the terms orbital- and spin-angular momentum date form these days.

In 1932 Robert S. Mulliken coined the noun "orbital". He wrote: From here on, one-electron orbital wave functions will be referred to for brevity as orbitals. Then he went on to distinguish atomic and molecular orbitals.

Later the somewhat unfortunate term "spinorbital" was introduced for the product functions φ(r₁)α(μ₁) and φ(r₁)β(μ₁) in which φ(r₁) has the tautological name "spatial orbital" and α(μ₁) and β(μ₁) are called "one-electron spin functions". The term "spinorbital" is unfortunate because it merges in one word the concepts of spin and orbital, which were distinguished carefully by early writers on quantum mechanics. For instance, one of the pioneers of theoretical chemistry, Walter Heitler, correctly contraposes two-electron spin functions and two-electron orbital functions. In the phrase two-electron orbital function, Heitler uses orbital as an adjective synonymous with spatial (non-spin). Note, parenthetically, that Heitler does not refer to a "two-electron orbital", (there is no such thing as a two-electron orbital!), but that an inexperienced reader may easily misread the term "two-electron orbital function" as "two-electron orbital".

Applications

Before the advent of electronic computers, orbitals (molecular as well as atomic) were used extensively in qualitative arguments explaining several properties of atoms and molecules. Orbitals still play this role in introductory texts and also in organic chemistry, where orbitals serve in the explanation of some reaction mechanisms, for instance in the Woodward-Hoffmann rules. In modern computational quantum chemistry the role of atomic orbitals is different; they serve as a convenient expansion basis, comparable to powers of x in a Taylor expansion of a function f(x), or sines and cosines in a Fourier series.

Atomic orbitals

Bohr was the first to see how atomic orbitals form a basis for an understanding of the Periodic Table of elements. In the explanation of the Periodic Table, atomic orbitals are labeled as if they are hydrogen orbitals, that is, by a principal quantum number n and a letter designating the azimuthal quantum number (angular momentum quantum number) l. This labeling is not only correct for hydrogen-like orbitals, but also for AOs that arise as solutions from an N-electron independent particle model with a central (spherically symmetric) potential field. A central field is necessary to have l as a good quantum number, and the concept "orbital" is tied to an independent particle model, such as the Hartree and the Hartree-Fock model.

In an independent particle model an Ansatz for the total N-electron wave function is a (possibly antisymmetrized) product of orbitals. From the effective-one-electron Schrödinger equation ensuing from this Ansatz, the actual forms of the orbitals and orbital energies are obtained, see Hartree-Fock method for an example and more details. Two major differences between such an effective-one-electron model and the analytic solution of the hydrogen atom are: (i) The radial functions are given numerically, and are no longer known analytic functions, such as the Laguerre functions for the hydrogen atom. The angular parts, however, are the same analytic functions as for the H-atom (spherical harmonics). (ii) The orbitals within a given atomic shell (orbitals with same pricipal quantum number n) are no longer degenerate (have no longer the same energy). While in the hydrogen atom, for instance the orbitals in the n = 3 shell: 3s, 3p, and 3d, all have the same energy (proportional to 1/n² = 1/3²), the degeneracy for the N-electron atom is lifted: only those of same azimuthal quantum number l are degenerate. The principal quantum number is now simply a counting index, it counts in increasing energy orbitals of the same l, starting at n = l + 1 (to be in line with the hydrogen AOs). It is found that the orbitals arising from the central field, independent particle model have the following order in increasing energy

1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 5s, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d.

Remark: for some atoms the order of 3d and 4s is flipped and for some other atoms the order of 4d and 5s is flipped.

One can now build up the atoms in the Periodic table by the Aufbau principle: fill orbitals in increasing energy. Obey the Pauli exclusion priciple that forbids more than two electrons per spatial orbital. Allowed is at most one electron with α spin and one with β spin. Recall further that there are 2l+1 orbitals of definite l. For instance, the neon atom (atomic number Z = 10) has the electronic configuration

${\scriptstyle 1s^{2}\,2s^{2}\,2p^{6},}$

while chlorine (Z = 17) has

${\scriptstyle 1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{5}\,}.$

For more details the article Periodic Table may be consulted.

Molecular orbitals

In the hands of Friedrich Hund, Robert S. Mulliken, John Lennard-Jones, and others, molecular orbital theory was established firmly in the 1930s as a (mostly qualitative) theory explaining much of chemical bonding, especially the bonding in diatomic molecules.

MO energy level diagram for H₂

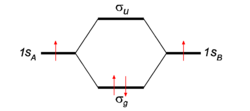
To give the flavor of molecular orbital theory we look at the simplest molecule: H₂. There two hydrogen atoms, labeled A and B. At infinite distance they have each one electron (a red arrrow) in an 1s atomic orbital. The AOs are labeled in the figure 1s_A and 1s_B. When then atoms start to interact these AOs combine linearly to two molecular orbitals:

$\sigma _{g}=N_{g}(1s_{A}+1s_{B})\quad {\hbox{and}}\quad \sigma _{u}=N_{u}(1s_{A}-1s_{B})$

Because both hydrogen atoms are identical there is reflection symmetry with respect to a mirror plane halfway the H—H bond and perpendicular to it. It is one of the basic assumptions in quantum mechanics that wave functions reflect the symmetry of the system. [Technically, they belong to a subspace of Hilbert (function) space that is irreducible under the symmetry group of the system]. Clearly σ_g is symmetric (stays the same) under

$\mathrm {\scriptstyle Reflection:} \quad 1s_{A}\longleftrightarrow 1s_{B},$

while σ_u changes sign (is antisymmetric). The notation σ indicates invariance under rotation around the bond axis. So, because of the high symmetry of the molecule we can immediately write down two molecular orbitals, which evidently are linear combinations of atomic orbitals. Only the normalization factors N_g and N_u must be computed.

(to be continued)

References and notes

(To be continued)