Energy (science)

Energy is a word with several connotations. The word goes back to the natural philosophy of Aristotle, ενέργεια (energeia), where it means roughly "efficacy". In the early nineteenth century the word was incorporated into science by Thomas Young. In science, the concept energy has a clear meaning, which, however, is not easy to explain because of the many forms in which energy manifests itself. The word energy is also very commonly used outside science, where it means physical or mental power to achieve something. "Negative energy" is a mental power that is in the way of achieving things.

In this article we will restrict attention to the scientific meaning of energy. In science, energy is a measurable property of a physical or chemical system, i.e., the energy of a system may be expressed by a single real number. Roughly speaking, the energy of a system is a measure of the amount of work that the system is able to perform on its environment. As stated, energy has many manifestations, be it chemical energy of a certain amount of gasoline, the kinetic energy of a moving cannon ball, the heat stored in a steam boiler, the potential energy of water in a reservoir, the fusion energy contained in a hydrogen bomb, the electricity in a battery. All these manifestations obey the same very important law: energy is conserved in conversion from one form of energy to the other. This law of conservation of energy is known as the first law of thermodynamics. This law pervades all of science, and is probably science's most important principle.

Let us consider an example. Assume we use a pump, running on gasoline, to pump water up to a reservoir, and when the reservoir is filled, we let the water flow down to drive an electrical generator. Doing this, we convert the chemical energy of the gasoline to (i) the mechanical energy of the pump to (ii) the potential energy of the water in the reservoir to (iii) the kinetic energy of the falling water, and finally to (iv) the electric energy generated by the generator. If we use the generated electric current for lighting, then the light bulbs convert the electric current to yet another form of energy, namely (v) light (electromagnetic radiation). During these energy conversion processes, the law of conservation of energy assures us that no energy is lost. To non-scientists the contrary may seem the case sometimes, because heat is generated (especially in burning the gasoline to drive the pump), and the heat will escape to the environment without any useful, or directly noticeable, effect. However, since heat is also a form of energy, it must be included in the energy balance of the first law.

Energy in classical mechanics

To keep the discussion simple we will consider a point particle of mass m in one-dimensional space. That is the position of m at time t is given by x(t). For more details and extension to the three-dimensional case, see classical mechanics. Let us assume that a force F(x) is acting on the particle. As an example we may think here of a mass in the gravitional field of the earth. The one dimensional space in this example is a line perpendicular to the surface of the earth. Actually, we will consider the slightly more complicated case of F being a function of x, because remember that the gravitational force F does not depend on x near the surface of the earth. (The expression for F close to the surface is: F = mg, where g is the gravitational acceleration, a constant of approximate value 9.8 m/s².)

So, the physical system that we are considering is the particle of mass m in a force field F(x). Earlier we defined energy as the work that a system can deliver to its environment. If work is done by the system its energy decreases. If work is done on the system its energy increases. Think now, for example, of Galileo Galilei (GG), carrying mass up the stairs of the leaning tower of Pisa. Doing this GG has the overcome the gravitational force, which works downward. The work ΔW performed by GG is proportional to the gain in height Δx and the absolute value |F| of the force. Since the work done by GG is positive and F is directed downward (F = − |F|), we have

$\Delta W=-F\Delta x\,,$

for the work done by GG on the system while carrying the mass up over a distance Δx. The gain in potential energy dU of the system is the work done on it by GG,

$dU=-Fdx\Longrightarrow U(x)=-\int _{x_{0}}^{x}\,F(x')\,dx',$

where we made the choice of zero of potential energy: $\scriptstyle U(x_{0})=0\,$. By the fundamental theorem of integral calculus, we have the important expression that relates force F(x) and potential energy U(x),

$F(x)=-{\frac {dU(x)}{dx}}.$

Besides potential energy, classical mechanics knows another form of energy: kinetic energy. Suppose GG drops the mass to the bottom of the tower after arriving at its top. The mass will pick up speed, (we will neglect air resistance, which will put some brake on the falling mass and generate some heat) and get the kinetic energy

$T\equiv {\tfrac {1}{2}}mv^{2}\quad {\hbox{with}}\quad v\equiv {\frac {dx}{dt}},$

where the speed of the particle is the absolute value of its velocity v.

This dropping of mass off the tower of Pisa is a good example of conversion of energy: potential energy is converted in kinetic energy. We will prove that energy is conserved, that is, the sum of kinetic and potential energy is constant in time.

${\frac {d}{dt}}(T+U)=mv{\frac {dv}{dt}}+{\frac {dU}{dx}}{\frac {dx}{dt}}=mva-Fv,\quad {\hbox{with}}\quad a\equiv {\frac {dv}{dt}}.$

Invoke Newton's second law (see classical mechanics):

$F=ma\,,$

and we have proven that the time derivative vanishes of the total energy E ≡ T + U of the physical system under consideration. That is, E is a conserved property of the system.

Finally, one may wonder what happens when the particle, dropped by GG from the top of the tower of Pisa, hits the ground. Here we have a collision of two bodies, the earth and the dropped particle. The collision can be elastic, in which case no energy is dissipated. If we take the mass of the earth to be infinite, the particle bounces up with the same kinetic energy that it had when it hit the earth. That is, its speed |v | remains the same, but the sign of v changes. The momentum mv of the particle changes by −2mv on collision, which seems contradictory to the law of conservation of momentum. The latter conservation law holds when there are no outside forces acting on our physical system consisting of the earth and the dropped particle. Since we implicitly assumed that no outside forces are present, we indeed expect conservation of momentum. To explain this apparent violation, we note that the earth receives the absolute value of momentum M|V | = 2m|v | from the collision, where M is the mass of the earth and V is the velocity of the earth gained by the collision. When M goes to infinity, V goes to zero. Hence, for infinite mass the earth absorbs momentum without changing velocity and without picking up kinetic energy. This is why the kinetic energy of the bouncing particle is conserved.

A collision may be inelastic: the particle may break up in pieces which fly off with kinetic energy and the earth will absorb the remaining kinetic energy of the falling particle. This absorption is by increase of the internal energy of the earth, which in general implies some warming up of the earth. Of course, the law of energy conservation still holds: the kinetic energy of the broken particle pieces and the increase of the internal energy of the earth add up to the kinetic energy of the dropped particle. As a final remark: most collisions are somewhere in between elastic and completely inelastic. The particle will bounce back some height, losing some kinetic energy that is transferred to the earth as an increase of the earth's internal energy.

Energy in thermodynamics

Heat

A thermodynamical system is a physical system with an extra property: temperature (T). When two thermodynamical systems of unequal temperature are in thermal contact, heat will flow from the warmest (highest temperature) system to the coldest (lowest temperature) system. This heat flow will decrease the temperature of the warmer system and increase the temperature of the colder. The heat flow will be sustained until equilibrium is reached and the two systems have the same temperature. At equilibrium the heat flow stops. Heat is a form of energy that flows spontaneously whenever there is a temperature difference between two systems that are in thermal contact.

Conversion of heat flow to work W.

Earlier we defined in a handwaving manner energy as the capacity of a system to do work. Now the question arises whether exchange of heat, which is an exchange of energy, can perform work. Or, in other words, can the energy content of a heat bath be utilized to perform work? It is clear that in any case two systems of different temperature are needed, otherwise heat will not flow. The first to recognize this clearly was William Thomson (Lord Kelvin).

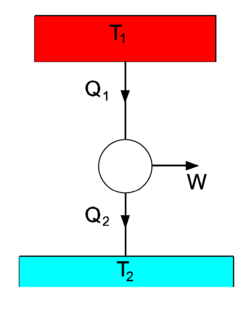
A heat flow is depicted in the figure on the right, where we see two heat baths, with T₁ > T₂. The circle in the middle designates a heat engine, a cyclic process in which heat is converted into work W. From the first law of thermodynamics follows that during a number of full cycles of the engine, no net energy is stored in the engine,

$Q_{1}-W-Q_{2}=0\Longrightarrow W=Q_{1}-Q_{2}.\qquad \qquad \qquad (1)$

The second law of thermodynamics states that

${\frac {Q_{2}}{T_{2}}}-{\frac {Q_{1}}{T_{1}}}\geq 0.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;(2)$

If we take the heat engine in the drawing to be the idealized Carnot engine that undergoes reversible changes, the equality sign holds. For the sake of argument we assume this to be the case. Multiplication of Eq. (2) by $\scriptstyle T_{2}/Q_{1}$ gives

${\frac {Q_{2}}{Q_{1}}}-{\frac {T_{2}}{T_{1}}}=0\Longrightarrow {\frac {Q_{2}-Q_{1}}{Q_{1}}}-{\frac {T_{2}-T_{1}}{T_{1}}}=0\Longrightarrow {\frac {W}{Q_{1}}}={\frac {T_{1}-T_{2}}{T_{1}}}.$

So, the work W is a fraction of the heat Q₁ delivered by the upper heat bath,

$W=\eta \,Q_{1}\quad {\hbox{with}}\quad \eta \equiv {\frac {T_{1}-T_{2}}{T_{1}}}\quad {\hbox{and}}\quad 0\leq \eta \leq 1.$

For instance, if T₁ = 500 ⁰C and T₂ = 20 ⁰C , then η = 480/(273.15+500) = 0.62. That is, at most 62% of the heat delivered by the upper heat bath is converted into work, the remaining energy is lost to the lower heat bath.

One may wonder why the work W is related here to Q₁. The answer is that the setup of the figure is a model for many engines. Historically, the model was first introduced for the steam engine. The upper heat bath is the steam boiler which is held at a constant temperature T₁ by burning fuel (in the days of the steam engine usually coal). During the cycle in the middle of the figure the steam drives a piston that performs work W. During this, the steam cools down, and the steam is cooled down even further in the condensor, becoming liquid water again. The condensor takes away the rest heat Q₂, which is not used any further, but given off to the environment (the lower heat bath of ambient temperature T₂). The condensed water is led back from the condensor to the steam boiler and heated again, completing the cycle. So, the heat flow between two reservoirs of unequal temperature (the steam boiler and the environment) generates work plus a rest energy Q₂. The arising of this rest energy has the consequence that only a fraction η of Q₁, the heat obtained from burning fuel, can be used to do work.

The same principles applies to combustion engines, for instance car engines, where the rest heat Q₂ is given off to the environment through the car radiator. The fact that only a fraction of the chemical energy stored in gasoline is converted into mechanical work (kinetic energy of the car) is not a design flaw, but a consequence of physical principles (the first and second law of thermodynamics).

The three arrows in the figure can be reverted, in which case the figure depicts a heat pump, for instance a refrigerator or an air conditioner. Work is delivered, usually by an electric motor, and heat Q₂ is drawn from the lower temperature bath (for instance, the inside of a refrigerator). The heat Q₁ is transported to the higher temperature heat bath (in the case of a refrigerator the air in the kitchen, in the case of an air conditioner the outside air). Here we see an illustration of the Clausius principle, it takes work W to extract the amount Q₂ of heat and this is converted into Q₁. Since a refrigerator gives off its heat to the kitchen, it cannot be used as an air conditioner. The work W done by its electric motor is converted into the net heat Q₁ − Q₂. Overall, the refrigerator acts as an electric heater, converting electric energy W > 0 into heat Q₁ − Q₂ > 0 that is given off to the surroundings of the refrigerator. By the same reasoning it is clear why an air conditioner needs an outlet outside the house for its rest heat.

Work

Besides being able to exchange heat, a thermodynamic system can do also work on another system or on its environment, which decreases its internal energy U. Conversely, another system, or the environment, can do work on the system, increasing U. Above we already assumed that the exchange of energy by work was possible for the Carnot engine. Work can be mechanical, electrical, magnetic, chemical, and so on.

The standard textbook example of mechanical work regards a gas filled cylinder with a piston on top. Let the pressure inside the cylinder be p, the surface of the piston be S and the volume of the cylinder be V. If the piston is moved into cylinder over a distance Δx, an amount of work ΔW is performed on the gas which is equal to F Δx. By the definition of pressure the force F is equal to pS, so that the work is ΔW = pSΔx = pΔV, where we assume that p is constant under the small displacement of the piston. The internal energy increases by ΔU, while V decreases by ΔV, so that

$\Delta U=-p\Delta V\,.$

If the piston moves outward, the volume increases, the system perfoms work on its surroundings, costing it internal energy, and hence the sign in the equation covers this case as well.

The work performed on, or by, the system is of the form aΔb, where a does not depend on the size of the system (when we halve the volume of the system and its gas content the pressure p stays the same). The quantity a is an intensive parameter. The quantity b is linear in the size of the system, it is an extensive parameter. This is a general form for all expressions for work, they always involve an intensive/extensive parameter couple. Another example is the polarisation P (a macroscopic dipole) of a dielectricum in a static electric field E. The work done by the field is EΔP. When we add an amount Δn mol of substance to a system, we increase its internal energy by μΔn, where μ is the chemical potential of the substance. This addition of substance can be seen as "chemical work" performed on the system. Even heat exchange fits this pattern, ΔQ = T ΔS, where the temperature T is an intensive and the entropy S is an extensive parameter.

Notes

(To be continued)