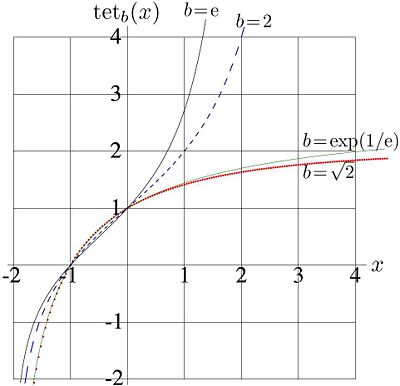
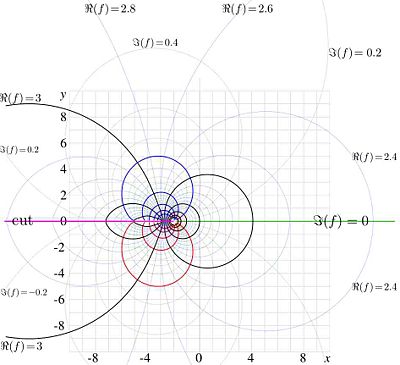
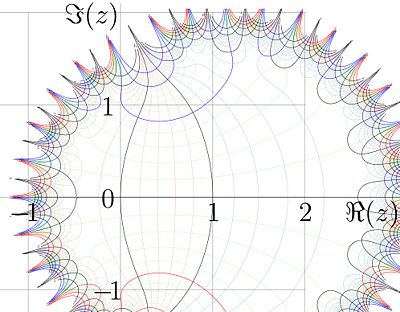
Fig.1. Tetration

for

,

,

, and

versus

.
Tetration is fastly growing mathematical function, which was introduced in XX century and suggested for representation of huge numbers in mathematics of computation. For positive integer values of its argument  , tetration
, tetration  on base
on base  can be defined with:
can be defined with:

For real values of the argument  and various values of base
and various values of base  , this
, this  is plotted in FIg.1.
is plotted in FIg.1.
Up to year 2008, this function is not listed among elementary functions, it is not implemented in programming languages and it is not used for the internal representation of data in computers.
In this article, the generalizaiton of tetration for complex (and, in particular, real) values of its argument is described.
Tetration is assumed to be holomorphic function, at least for positive values of the real part of its argument.
This tetration is used to construct the holomorphic extension of the iteratied exponential  for the case of non-integer values of the number
for the case of non-integer values of the number  of iterations.
of iterations.
Definiton
For real  , Tetration
, Tetration  on the base
on the base  is function of complex variable, which is holomorphic at least in the range
is function of complex variable, which is holomorphic at least in the range
 , bounded in the range
, bounded in the range
 , and satisfies conditions
, and satisfies conditions



at least within range  .
.
The definition above generalizes the definitions suggested recently for the specific cases of base  [1] and
[1] and  [2].
[2].
Etymology and place of tetration in the big picture of math
Creation of word tetration is attributed to Englidh mathematician Reuben Louis Goodstein
[3].
The place of tetration in the mathematical analysis can be seen at the strong zoom-out of the big picture of math.
Using the mathematical notations, the zoom-out of the mathematical analysis can be drawn as follows:
 has only one argument and means unitary increment
has only one argument and means unitary increment ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
; 
Except the zeroth raw, each operation in sequance above is just recurrence of operations from the previous row.
Operation ++ could be called zeration (although in the prigramming languages it is called increment),
addition (or summation) could be called unation,
multiplication (or product) could be called duation ,
exponentiation coluld be called trination.
The following operations ( tetration, pentation) are not used so often, at least up to year 2008. Although
tetration could get many other names:
superexponentiation [4], ultraexponent [5], generalized exponent [6],
other names were not applied to the holomorphic extension of tetration, defined in the previous section.
Manipulation with the holomorphic extensions and the inverses of summation, multiplication, exponentiation form the core of the mathematical analysis.
The table above shows the place of tetration in the big picture of math. It is up-to-last raw.
In such a way, the name tetration indicates, that this operation is fourth (id est, tetra) in the hierarchy of operations after summation, multiplication, and exponentiation. In principle, one can define "pentation", "sextation", "septation" in the simlar manner, although tetration, perhaps, already has growth fast enough for the requests of XXI century.
Real values of the arguments, general view
Examples of behavior of this function at the real axis are shown in figure 1 for values
 ,
,
 ,
,
 , and for
, and for
 . It has logarithmic singularity at
. It has logarithmic singularity at  , and it is monotonously increasing function.
, and it is monotonously increasing function.
At  tetration
tetration  approaches its limiting value as
approaches its limiting value as
 , and
, and  .
.
Fast growth and application
At  tetration
tetration  grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation[4].
A number, that cannot be stored as floating point, could be represented as
grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation[4].
A number, that cannot be stored as floating point, could be represented as  for some standard value of
for some standard value of  (for example,
(for example,  or
or  ) and relatively moderate value of
) and relatively moderate value of  . The analytic properties of tetration could be used for the implementation of arithmetic operations with huge numbers without to convert them to the floating point representation.
. The analytic properties of tetration could be used for the implementation of arithmetic operations with huge numbers without to convert them to the floating point representation.
Integer values of the argument
For integer  , tetration
, tetration  can be interpreted as iterated exponential:
can be interpreted as iterated exponential:



and so on; then, the argument of tetration can be interpreted as number of exponentiations of unity. From definition it follows, that

and

At base  , tetration is related to the Ackermann function [7]
, tetration is related to the Ackermann function [7]

where Ackermann function  is defined for the non-negative integer values of its arguments with equations
is defined for the non-negative integer values of its arguments with equations

The generalization of the 4th Ackermann funciton  for the complex values of
for the complex values of  is described in the preprint [2] . Construction of such holomorphic extension is equivalent to construction
of tetration
is described in the preprint [2] . Construction of such holomorphic extension is equivalent to construction
of tetration  for the base
for the base  .
.
Asymptotic behavior and properties of tetration
The analytic extension of tetration  grows fast along the real axis of the complex
grows fast along the real axis of the complex  -plane, at least for some values of base
-plane, at least for some values of base  . However, it does not grow infinitely in the direction of imaginary axis.
The asymptotic behavior determines the basic properties of tetration.
. However, it does not grow infinitely in the direction of imaginary axis.
The asymptotic behavior determines the basic properties of tetration.
The exponential convergence of discrete interation of logarithm corresponds to the exponential asymptotic behavior

where
 ,
,
 and
and  are fixed complex numbers,
and
are fixed complex numbers,
and  is eigenvalue of logarithm, solution of equation
is eigenvalue of logarithm, solution of equation
 .
.
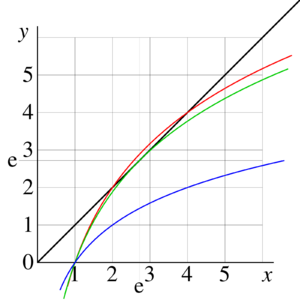
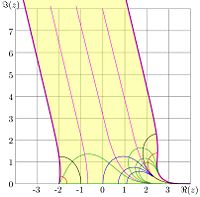
FIg.2. Graphic solution of equation

for

(two real solutions,

and

),

(one real solution

)

(no real solutions).
Solutions of this equation are called fixed points of logarithm.
Fixed points of logarithm
Three examples of graphical solution of equation for fixed points of logarithm are shown in figure 2 for
 ,
,
 , and
, and
 .
.
The black line shows function  in the
in the  plane.
The colored curves show function
plane.
The colored curves show function  for cases
for cases
 (red),
(red),
 (green), and
(green), and
 (blue).
(blue).
At
 , there exist 2 solutions,
, there exist 2 solutions,
 and
and
 .
.
At
 there exist one solution
there exist one solution
 .
.
and  , there are no real solutions.
, there are no real solutions.
In general,
- at
 , there are two real solutions;
, there are two real solutions;
- at
 , there is one soluition, and
, there is one soluition, and
- at
 , there exist two solutions, but they are complex.
, there exist two solutions, but they are complex.
In particular,
at
 , the solutions are
, the solutions are
 and
and

.
At
 , the solutions are
, the solutions are
 and
and
 .
.
At  , the solutions are
, the solutions are
 and
and
 .
.
Few hundred straightforward iterations of equation (14) are sufficient to get the error smaller than the last decimal digit in the approximations above.
Basic properties
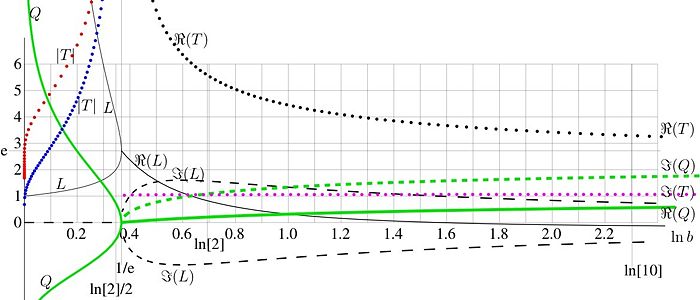
FIg.3. parameters of asymptotic of tetration versus logarithm of the base
The solutions
 and
and
 of equation (14) are plotted in figure 3 versus
of equation (14) are plotted in figure 3 versus
 with thin black lines. Let
with thin black lines. Let
 , and only at
, and only at
 , the equality
, the equality
 takes place.
Basic properties of tetration are determined by the base
takes place.
Basic properties of tetration are determined by the base  . The main parameters versus
. The main parameters versus
 are plotted in figure 3.
The thin black solid curve at
are plotted in figure 3.
The thin black solid curve at
 represents the real part of the solutions
represents the real part of the solutions
 and
and
 of (14); the thin black dashed curve represents the two options for the imaginary part; the two solutions are complex conjugaitons of each other.
Requirement of definition of tetration determine the asymptotic of the solution. Parameter
of (14); the thin black dashed curve represents the two options for the imaginary part; the two solutions are complex conjugaitons of each other.
Requirement of definition of tetration determine the asymptotic of the solution. Parameter  tetermines periodicity of quasi-periodicity of tetration. The two solutions for
tetermines periodicity of quasi-periodicity of tetration. The two solutions for  are shown in figure 3 with green lines.
are shown in figure 3 with green lines.
At  both solutons for
both solutons for  are real. The negative
are real. The negative  corresponds to tetration, decaying to the asymptotic value
corresponds to tetration, decaying to the asymptotic value  in the direction of real axis; positive
in the direction of real axis; positive  corresponds to the solution growing along the real axis. At the real axix, such a solution remains larger than unity; this does not allow to satisfy confition
corresponds to the solution growing along the real axis. At the real axix, such a solution remains larger than unity; this does not allow to satisfy confition  . Therefore, only one negative
. Therefore, only one negative  corresponds to the asymptotic behavior of tetration.
corresponds to the asymptotic behavior of tetration.
At  , both options for
, both options for  are mutually complex conjugate. The real part is shown thif thick green line; one option of the imaginary part is shown with dashed line.
are mutually complex conjugate. The real part is shown thif thick green line; one option of the imaginary part is shown with dashed line.
Possibilities for the period (or quasi-period)  are shown in Figure 3 with fotted lines. At
are shown in Figure 3 with fotted lines. At  , only "negative" period corresponds to tetration. At
, only "negative" period corresponds to tetration. At  , the periodicity can be achieved only asymptotically; and
, the periodicity can be achieved only asymptotically; and  is quasi-period. The real part of quasi-period is markes with black dotted line; one of two options tor the imaginary part is marked with pink dotted line.
is quasi-period. The real part of quasi-period is markes with black dotted line; one of two options tor the imaginary part is marked with pink dotted line.
Generally, at  , tetration is periodic; the period is pure imaginary.
, tetration is periodic; the period is pure imaginary.
At  , tetration is not periodic, and no exponential asymptotic exist.
, tetration is not periodic, and no exponential asymptotic exist.
 , tetration is quasi–periodic, the quasi-period in the upper complex half-plane is conjugate to that in the lower complex half-plane. The larger is base
, tetration is quasi–periodic, the quasi-period in the upper complex half-plane is conjugate to that in the lower complex half-plane. The larger is base  , the shorter is quasi-period. As the quasi-periods are complex conjugated, the quasi-periodicity takes place away from the real axis.
, the shorter is quasi-period. As the quasi-periods are complex conjugated, the quasi-periodicity takes place away from the real axis.
Evaluation of tetration
As the asymptoric of tetration is crutually depend of base  in ficinity of
value
in ficinity of
value  , the evaluation procidure is different foe the cases
, the evaluation procidure is different foe the cases
 ,
,  , and
, and  , and should be considered serapately.
, and should be considered serapately.
Case 
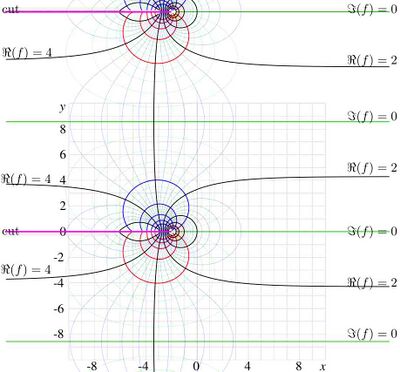
Fig.4. Tetration

for

At  , the period
, the period  is imaginary.
Period with smallest modulus corresponds to the solution that is unity at the origen of coordinates. For
is imaginary.
Period with smallest modulus corresponds to the solution that is unity at the origen of coordinates. For  , function
, function  is shown in figure 4 with levels of constant real part and levels of constant imaginary part. Levels
is shown in figure 4 with levels of constant real part and levels of constant imaginary part. Levels
 and levels
and levels
 aew shown with thick lines. Intermediate levels are shown with thin lines. There are branch points at
aew shown with thick lines. Intermediate levels are shown with thin lines. There are branch points at
 ; the cut lines are
; the cut lines are
 . For this value of base, the period
. For this value of base, the period
- Failed to parse (syntax error): {\displaystyle T=\frac{2\pi}{\ln^2(2)}\approx −17.1431481793548471041794 ~\mathrm{i}}
.
There is cut at  ,
,  ; although the jump at this cut reduces at the increase of
; although the jump at this cut reduces at the increase of  . In such a way, the function approaches its limiting value
. In such a way, the function approaches its limiting value  almost everywhere, although there is set of singularities at negiative integer values of
almost everywhere, although there is set of singularities at negiative integer values of  .
.
The solution follows asymptotic at large values of real part of the argument, exponentially approaching the limiting value. In particular, for  , this maximum limiting value is in the left hand side of the figure, and to its minimum llimiting value in the right hand side. For
, this maximum limiting value is in the left hand side of the figure, and to its minimum llimiting value in the right hand side. For
 , these limiting values are
, these limiting values are
 and
and
 .
.
The trace of the solution along the real axis corresponds to the red dotted curve in Figure 1.
Other solutions of the recursive equation  ,
that may grow up along the real axis, can be constructed in the similar way, but they do not satisfy criteria formulated in the definition of tetration; in particular,
,
that may grow up along the real axis, can be constructed in the similar way, but they do not satisfy criteria formulated in the definition of tetration; in particular,  .
.
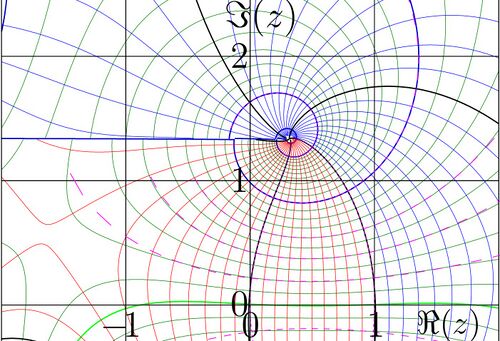
Case 
(CC) Image: Dmitrii Kouznetsov Fig.5. Tetration at

.
At  , the liniting value
, the liniting value  , and, asymptotically,
, and, asymptotically,

The function  is shown in figure 5.
is shown in figure 5.
Levels  are shown with thick black lines.
are shown with thick black lines.
Levels  are shown with thick red lines.
are shown with thick red lines.
Levels  are shown with thick blue lines.
are shown with thick blue lines.
Intermediate levels are shown with thin lines.
There is cut at  ,
,  , but the hump of the function at the cut reduces as
, but the hump of the function at the cut reduces as
 reduces, id est, with increasing of
reduces, id est, with increasing of  . In suchg a way, everywhere, at
. In suchg a way, everywhere, at
 , the function approaches its limiting value
, the function approaches its limiting value  .
almost everywhere, although there is set of singularities at negiative integer values of
.
almost everywhere, although there is set of singularities at negiative integer values of  .
.
Behavior of this function at real values of argument is shown in Figure 1 with thin solid line.
Other solutions of the recursive equation  can be constructed in the ximilar way; they may grow up along the real axis, but they do not satisfy criteria formulated in the definition of tetration; in particular,
can be constructed in the ximilar way; they may grow up along the real axis, but they do not satisfy criteria formulated in the definition of tetration; in particular,  .
.
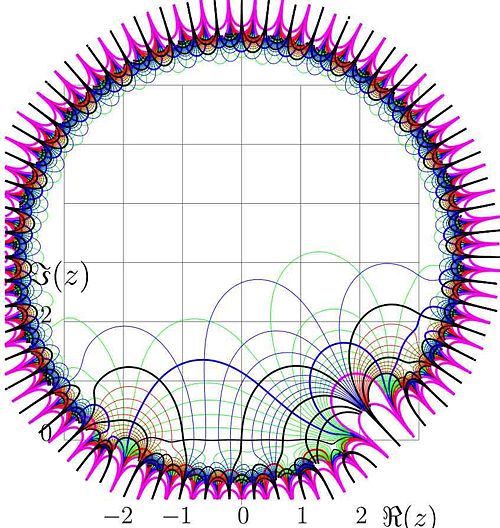
Case 
(CC) Image: Dmitrii Kouznetsov Fig.6. Tetration

at base

and

.
At  , tetration is asymptotically periodic. It exponentially
decays to the fixed points
, tetration is asymptotically periodic. It exponentially
decays to the fixed points  and
and  in th eupper and lower halfplane. This allows to express it through its values along the imaginary axis, using the Cauchi integral. [1].
in th eupper and lower halfplane. This allows to express it through its values along the imaginary axis, using the Cauchi integral. [1].
For the base  and
and  tetration
tetration
 is plotted in figure 6. Levels
is plotted in figure 6. Levels
 and
and
 are drawn with thick lines. The function has logarithmic singulatiry at point -2 and cut at real values of the argument, smaller than -2. In the right hand side, symbols
are drawn with thick lines. The function has logarithmic singulatiry at point -2 and cut at real values of the argument, smaller than -2. In the right hand side, symbols  mean huge values that cannot be stored in the conventional floating point representation (logarithm, mantissa). In the upper left and lower left part of eath graphic, the function approaches its asymptotic values
mean huge values that cannot be stored in the conventional floating point representation (logarithm, mantissa). In the upper left and lower left part of eath graphic, the function approaches its asymptotic values  and
and  . Function is quasi-periodic; the same fractal structure
reproduces again and again at the translation of argument with quasiperiod
. Function is quasi-periodic; the same fractal structure
reproduces again and again at the translation of argument with quasiperiod  in the upper halfplane and
in the upper halfplane and
 in the lower halfplane.
in the lower halfplane.
There is cut at  ,
,  . The jump of the function at this cut approaches
. The jump of the function at this cut approaches
 almost everywhere, although there is set of singularities at negiative integer values of
almost everywhere, although there is set of singularities at negiative integer values of  .
.
Along the real axis, tetration for this values of base is plotted also in figure 1 with thick solid and dashed lines.
Behavior along the real axis
The growth of tetration along the real axis is crutially determient by its base.
At  the growth is limited by the minimal of the limiting values
the growth is limited by the minimal of the limiting values
 . Tetration approaches this limiting value exponentially.
. Tetration approaches this limiting value exponentially.
At  , the growth is limited by the fixerd point
, the growth is limited by the fixerd point
 . Tetration approaches this limiting value as rational function.
. Tetration approaches this limiting value as rational function.
The growing-up holomorphic solution of equation  can be constructed in the similar way also at
can be constructed in the similar way also at
 , but at the real axis, such a solution remains larger than unity, and the condition
, but at the real axis, such a solution remains larger than unity, and the condition  cannot be satiscied. Therefore, this solution cannot be interpreted as extension of
iterative exponentiation
cannot be satiscied. Therefore, this solution cannot be interpreted as extension of
iterative exponentiation  for non-integer number
for non-integer number  of exponentiations; in this sense, such a solution is not a tetration.
of exponentiations; in this sense, such a solution is not a tetration.
Tetration  shows explosively-fast growth along the real axis
only at values
shows explosively-fast growth along the real axis
only at values  .
.
Tetration at base e
Holomorphyc tetration on the narutal base  is most developed, at least up to yeat 2008.
In the rest of this article, it is assumer that
is most developed, at least up to yeat 2008.
In the rest of this article, it is assumer that  although the most of results allow the straightforward extension to the case of real
although the most of results allow the straightforward extension to the case of real  .
.
Inverse of tetration

(CC) Image: Dmitrii Kouznetsov Fig.7. kslog in the complex plane.
The inverse of tetration  can be performed using the Newton method, solving equation
can be performed using the Newton method, solving equation  , leading to
, leading to
 .
.
The inverse function has branchpints  and
and  . For the kslog, at base
. For the kslog, at base  , shown in the figure 7, the cuts are placed horisontaly, along the lines
, shown in the figure 7, the cuts are placed horisontaly, along the lines
 ,
,  .
.
Due to the symmetry  , it is sufficient to plot only half of the complex plane.
, it is sufficient to plot only half of the complex plane.
(CC) Image: Dmitrii Kouznetsov Fig.8. Shaded region is image of the upper halfplane at the mapping with kslog function.
The mapping with function kslog is shown in figure 8. For  in the shaded region, the relation
in the shaded region, the relation

takes place. The upper part of the complex plane is mapped into the upper halfplane, and the lower halfplane is mapped to the lower halfplane. The real axis is mapped into the halfline  . The fixed points
. The fixed points
 is mapped to imaginary infinity, following the shadower strip.
is mapped to imaginary infinity, following the shadower strip.
In figure 8, the images of the grid lines  and
images of the grid lines
and
images of the grid lines  are shown. These curves reproduce levels
are shown. These curves reproduce levels
 and
and
 shown in figure 6 for
shown in figure 6 for  .
.
Together, the pair of functions tet and kslog allow to evaluate any iteration (including negative, fractional and even complex) of the exponential finction.
Polynomial approximation
The Tailor expansion for the tetration can be written in the usial form:

where the  th coefficient
th coefficient

is expressed through the  derivative of the function.
The coefficients of the expansion can be calculated ising the straightforward differentiation of the representation through the Cauchi integral.
derivative of the function.
The coefficients of the expansion can be calculated ising the straightforward differentiation of the representation through the Cauchi integral.
Tailor expansion at zero

Fig.N. Approximation of tetration with polynomial of 25th power
For  , the calcuation gives the following values
, the calcuation gives the following values
 0 = 1
0 = 1 1 ≈ 1.091767351258322138
1 ≈ 1.091767351258322138 2 ≈ 0.271483212901696469
2 ≈ 0.271483212901696469 3 ≈ 0.212453248176258214
3 ≈ 0.212453248176258214 4 ≈ 0.069540376139988952
4 ≈ 0.069540376139988952 5 ≈ 0.044291952090474256
5 ≈ 0.044291952090474256 6 ≈ 0.014736742096390039
6 ≈ 0.014736742096390039 7 ≈ 0.008668781817225539
7 ≈ 0.008668781817225539 8 ≈ 0.002796479398385586
8 ≈ 0.002796479398385586 9 ≈ 0.001610631290584341
9 ≈ 0.001610631290584341 10≈ 0.000489927231484419
10≈ 0.000489927231484419 11≈ 0.000288181071154065
11≈ 0.000288181071154065 12≈ 0.000080094612538551
12≈ 0.000080094612538551 13≈ 0.000050291141793809
13≈ 0.000050291141793809 14≈ 0.000012183790344901
14≈ 0.000012183790344901 15≈ 0.000008665533667382
15≈ 0.000008665533667382 16≈ 0.000001687782319318
16≈ 0.000001687782319318 17≈ 0.000001493253248573
17≈ 0.000001493253248573 18≈ 0.000000198760764204
18≈ 0.000000198760764204 19≈ 0.000000260867356004
19≈ 0.000000260867356004 20≈ 0.000000014709954143
20≈ 0.000000014709954143 21≈ 0.000000046834497327
21≈ 0.000000046834497327 22≈-0.000000001549241666
22≈-0.000000001549241666 23≈ 0.000000008741510781
23≈ 0.000000008741510781 24≈-0.000000001125787310
24≈-0.000000001125787310 25≈ 0.000000001707959267
25≈ 0.000000001707959267
The truncated Tailor series gives the polyomial approximation.
In Figure N, the polynomial

is shown in the complex  plane.
plane.
- Levels
 are shown with thick black curves.
are shown with thick black curves.
- Levels
 are shown with thin red curves.
are shown with thin red curves.
- Levels
 are shown with thin thin blue curves.
are shown with thin thin blue curves.
- Levels
 are shown with thick red curves.
are shown with thick red curves.
- Levels
 are shown with thick blue curves.
are shown with thick blue curves.
- Levels
 are shown with thick pink curves.
are shown with thick pink curves.
- Levels
 are shown with thin green curves.
are shown with thin green curves.
In the upper left corner of figure N, the same is shown for function 
At the botton, left, the overlap of the upper two images is shown.
At the botton, right, lines of constant modulus and constant phase of holomorphic tetration in the same range.
The good approximation of tetration takes place in the range  of order of unity or smaller; the radius of convergence of the series is 2.
of order of unity or smaller; the radius of convergence of the series is 2.
Expansion at 3i
Tailor expansion ot tetration developed at 3i, truncated at 30th power, plotted in the complex plane.
Coefficients of the expansion

can be evaluated in the similar way:































The plot of approximation of tetration with the resulting polynomial of 30th power is shown in figure
Asymptotic expansion at large values of the imaginary part of the argument

Fig.As. Deviation of tetration from its asymptotic expansion.
Here only case of base  is considered; although the generalization for the case
is considered; although the generalization for the case  is straghtforward. In this section, the bevavior of tetration
is straghtforward. In this section, the bevavior of tetration
 is considered for the moderate values of
is considered for the moderate values of
 and large values of
and large values of 
At  , in the upper halfplane, tetration approach the fixed point
, in the upper halfplane, tetration approach the fixed point
 of the logarithm. This approach is exponential. Using the exponential
of the logarithm. This approach is exponential. Using the exponential

as a small parameter, for some complex constant  , the tetration can be estimated as follows:
, the tetration can be estimated as follows:

Substitution of this expression into the equation  gives
gives


Value  can be found fitting the tetration
can be found fitting the tetration
 with function
with function  at large values of
at large values of
 . Then, the expansion can be written in the form
. Then, the expansion can be written in the form

assuming that  and
and  . At given
. At given  , such a representation
indicates the possible approximations of tetration. The deviations od tetration from these approximations are shown in figure Fig.As.
, such a representation
indicates the possible approximations of tetration. The deviations od tetration from these approximations are shown in figure Fig.As.
The four plots in fig.As correspond to the four asumptotic approximations. The deviations
 ,
, ,
, ,
,
are shown in the complex plane with lines of constant phase and constant modulus.
- Levels
 are shown with thick red lines.
are shown with thick red lines.
- Level
 is shown with thick black lines.
is shown with thick black lines.
- Levels
 are shown with thick blue lines.
are shown with thick blue lines.
- Levels
 are shown with scratched lines. (these lines reveal the step of sampling used by the plotter).
are shown with scratched lines. (these lines reveal the step of sampling used by the plotter).
- Levels
 are shown with thin red lines.
are shown with thin red lines.
- Levels
 are shown with thin blue lines.
are shown with thin blue lines.
- Levels
 are shown with thin thick black lines.
are shown with thin thick black lines.
- Level
 is shown with thick red line.
is shown with thick red line.
- Levels
 are shown with thick black lines.
are shown with thick black lines.
- Level
 is shown with thick red line.
is shown with thick red line.
- Levels
 are shown with thick black lines.
are shown with thick black lines.
- Level
 is shown with thick green line.
is shown with thick green line.
- Level
 is shown with thick black line.
is shown with thick black line.
The plotter tried to draw also
- Level
 with thick black line and
with thick black line and
- Level
 with thin dark green line, which are seen a the upper left hand side corners of the two last pictures, but the precision of evaluation of tetration is not sufficient to plot the smooth lines; for the same reason, the curve for
with thin dark green line, which are seen a the upper left hand side corners of the two last pictures, but the precision of evaluation of tetration is not sufficient to plot the smooth lines; for the same reason, the curve for
 in the last picture, in the upper right band side looks a little bit irreguler; also, the pattenn in the upper left corner of the last two pictures looks chaotic; the plotter cannot distinguish the function from its asymptotic aproximation.
in the last picture, in the upper right band side looks a little bit irreguler; also, the pattenn in the upper left corner of the last two pictures looks chaotic; the plotter cannot distinguish the function from its asymptotic aproximation.
The figure indicates that, at  ,
,  , the asymptotic approximation
, the asymptotic approximation

gives at least 14 correct significant figures. At large values of the imaginary part, this approximation is more precise than the evaluation of tetration through the contour integral.
Approximation of tetration with rational functions
Due to recurrent relation  , it is sufficient to approximate tetration in any vertical strip of unit with in the complex plane. Some of such approximations are suggested in [1],
, it is sufficient to approximate tetration in any vertical strip of unit with in the complex plane. Some of such approximations are suggested in [1],
Approximation of slog
Function slog, which is inverse of tetration, allows the approximation with elementary functions.
Tailot expansion
Approximation of slog with polynomial of 16th power from the Tailor expansion at unity.
Expansion at fixed point  of logarithm
of logarithm
Fitting of slog with the expansion around

.
Superlogarithm can be approximated with expansion [8]
 ,
,
where  is fixed point of logarithm. This expansion indicates the ways to construct the asymptotic approximations of slog.
The coefficients can be expressed from the asymptotical analysis of equation
is fixed point of logarithm. This expansion indicates the ways to construct the asymptotic approximations of slog.
The coefficients can be expressed from the asymptotical analysis of equation  . Also, they can be expressed from the asymptotical estimate of tetration at large values of the imaginary part of the argument.
The evaluation of first coefficients gives
. Also, they can be expressed from the asymptotical estimate of tetration at large values of the imaginary part of the argument.
The evaluation of first coefficients gives





These coefficients allow to approximate slog in vicinity of the fixed point of logarithm with function
 .
.
In the figure this  is shown in the compled
is shown in the compled  -plane.
-plane.
- Levels
 are shown with thick black lines.
are shown with thick black lines.
- Levels
 are shown with thin red lines.
are shown with thin red lines.
- Levels
 are shown with thin dark green lines.
are shown with thin dark green lines.
- Levels
 is shown with thick green line.
is shown with thick green line.
(Deviation of this line from the real axis indicates the error of the approximation.)
- Level
 is shown with thick red line
is shown with thick red line
- Levels
 are shown with thin dark blue lines lines.
are shown with thin dark blue lines lines.
For comparison, dashed lines show the precise evaluation for some of the levels above for the robust implementation of the slog function as inverse of tetration. While  , the deviation of these dashed lines from the levels for function
, the deviation of these dashed lines from the levels for function  is not seen even at the strong zooming-in of the central part of the figure.
is not seen even at the strong zooming-in of the central part of the figure.
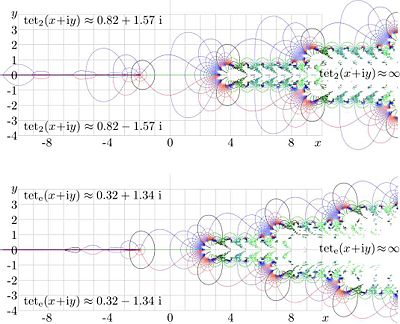
Iterated exponential and 
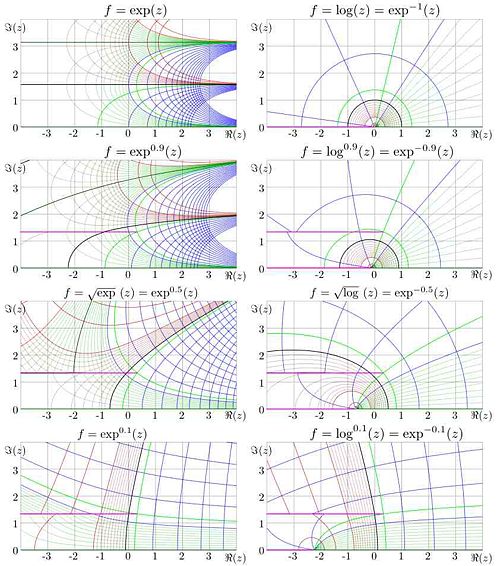
Fig.9.

in the complex

plane for various

.
Pre-historic approach to the iterated exponential
Especially interesting is the case of iteration of natural exponential, id est,  . Existence of the fractional iteration, and, in particular, existence of operation
. Existence of the fractional iteration, and, in particular, existence of operation  was demonstrated in 1950 by H.Kneser. [8].
However, that time, there was no computer facility for the evlauation of such an exotic function
was demonstrated in 1950 by H.Kneser. [8].
However, that time, there was no computer facility for the evlauation of such an exotic function
 that
that  ; perhaps, just absence of an apropriate plotter did not allow Kneser to plot the distribution of fractal exponential function
; perhaps, just absence of an apropriate plotter did not allow Kneser to plot the distribution of fractal exponential function
 in the complex
in the complex  plane for various values of
plane for various values of  , shown in Fig.9.
, shown in Fig.9.
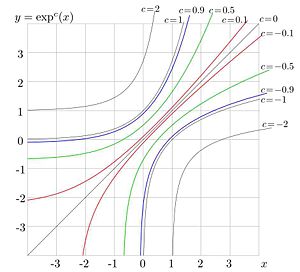
Fig.10.

versus

The Implementation through the tetration
Holomorphic tetration allows to extend the iterated exponential 




For non-integer values of  . It can be defined as
. It can be defined as

If in the notation  the superscript is omitted, it is assumed to be unity; for example
the superscript is omitted, it is assumed to be unity; for example
 . If the subscript is omitted, it is assumed to be
. If the subscript is omitted, it is assumed to be  , id est,
, id est, 
Iterated exponential in the complex plane
Function  is shown in figure 9 with levels of constant real part and levels of constant imaginary part. Levels
is shown in figure 9 with levels of constant real part and levels of constant imaginary part. Levels
 and
and
 are drown with thick lines.
Red corresponds to a negative value of the real or the imaginaryt part, black corresponds to zero, and blue corresponds to the positeive values.
Levels
are drown with thick lines.
Red corresponds to a negative value of the real or the imaginaryt part, black corresponds to zero, and blue corresponds to the positeive values.
Levels  are shown with thin red lines.
Levels
are shown with thin red lines.
Levels  are shown with thin green lines.
Levels
are shown with thin green lines.
Levels  and
Levels
and
Levels  are marked with thick green lines, where
are marked with thick green lines, where  is fixed point of logarithm.
At non-integer values of
is fixed point of logarithm.
At non-integer values of  ,
,  and
and  are branch points of function
are branch points of function  ; in figure, the cut is placed parallel to the real axis. At
; in figure, the cut is placed parallel to the real axis. At  there is an additional cut which goes along the negative part of the real axis. In the figure, the cuts are marked with pink lines.
there is an additional cut which goes along the negative part of the real axis. In the figure, the cuts are marked with pink lines.
Iterated exponential of a real argument
For real values of the argument, function  is ploted in figure 10 versus
is ploted in figure 10 versus  for values
for values
 .
.
in programming languages, inverse function of exp is called log.
For logarithm on base e, notation ln is also used. In particular,
 ,
,
 and so on.
and so on.
At least for the real and big enough  , the relation
, the relation  holds, which is qute analogous of relations
holds, which is qute analogous of relations
 and
and  .
However, at negative
.
However, at negative  or negative
or negative  , value
, value  should be big enough, that
should be big enough, that
 and
and
 and
and
 are defined, see figure 10. For example, at
are defined, see figure 10. For example, at  , we need
, we need  .
In particular, at
.
In particular, at  ,
,  , we have
, we have
 .
.
Applicaiton of iterated exponential
The iterated exponential, that can be implemented with holomorphic tetration, may have various applicaitons. In particular,
The  at </math>0\!<\!c\!<\!1</math> could describe a process that grows faster than any polynomial, but slower than any exponential. In such a way, the iterated exponential, at the proper implementation, should greatley extend the abilities of fast and precise fitting of functions. This is just analogy of function
at </math>0\!<\!c\!<\!1</math> could describe a process that grows faster than any polynomial, but slower than any exponential. In such a way, the iterated exponential, at the proper implementation, should greatley extend the abilities of fast and precise fitting of functions. This is just analogy of function  which, at fractal values of
which, at fractal values of  , may be good for description of a function that grows faster than any linear function but slower than any quadratic function.
, may be good for description of a function that grows faster than any linear function but slower than any quadratic function.
Similar functions
WIthdrowal of some of requirements from the definition of tetration allows the huge variety of similar functions.
Entire solutions of 
Withdrowal of the requirement  and
and  allows the solution by Kneser [8], which is entire and also could be used to buld up various powers of the exponential; in particular,
allows the solution by Kneser [8], which is entire and also could be used to buld up various powers of the exponential; in particular,  . Such entire function is shown in upper part of figure 1c in [1], in order to reveal the asymptotic henavior of holomotphic tetration.
. Such entire function is shown in upper part of figure 1c in [1], in order to reveal the asymptotic henavior of holomotphic tetration.
WIthdrowal of condition  allows to construct solutions, similar to the growing tetration, for base
allows to construct solutions, similar to the growing tetration, for base  . Although such solutions cannot be interpreted as generalization of exponential iterated
. Although such solutions cannot be interpreted as generalization of exponential iterated  times, they can be useful for generalization of exponential function.
times, they can be useful for generalization of exponential function.
Non-holomorphic modificaiton of tetration
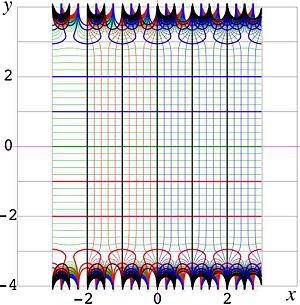
Fig.11. Almost identical function

in the complex

plane.
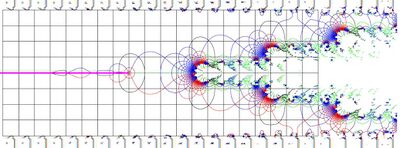
Fig.12. Motified tetration at the complex plane.
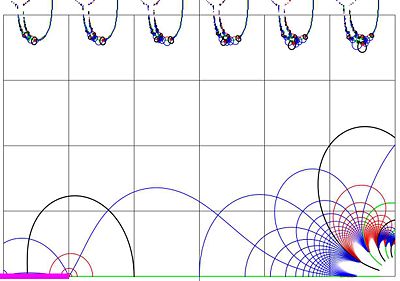
Fig.13. Zoom in of fig.12
WIthdrowal of requirement of holomorphicity from the definition of tetration allows functions, which look like the tetration, at least along the real axis. Even the reduction of the range of holomorphism in the requirement allows to consider tetration with modified argument. The modified tetration can be defined as
 ,
,
where  , and
, and  is a 1-periodic function. The simple example of such such function is
is a 1-periodic function. The simple example of such such function is

In this case, along the real axis, the function  is almost identical to its argument; and values of the modified tetration are close to values of tetration. Being plotted at figure 1 or in figure 10, the deviation of such function
is almost identical to its argument; and values of the modified tetration are close to values of tetration. Being plotted at figure 1 or in figure 10, the deviation of such function  from the identity is small, and the deviation of the modified tetration from tetration is also small. If the figures are printed in the real scale, then the defiation of the curves would be of order of atomic size.
from the identity is small, and the deviation of the modified tetration from tetration is also small. If the figures are printed in the real scale, then the defiation of the curves would be of order of atomic size.
However the difference becomes seen at the complex values of the argument.
In figure 11, function  is plotted in the complex
is plotted in the complex  plane.
Levels of constant real part and those of constant imajinary part are drawn. In vicinity of the real axis, these lines almost coincide with the gridline; the grid is drawn with step unity and extended one step to the right and one step to the left ftom the graphic. in order to show that it behaves as it if would be a continuation of the plot. At
plane.
Levels of constant real part and those of constant imajinary part are drawn. In vicinity of the real axis, these lines almost coincide with the gridline; the grid is drawn with step unity and extended one step to the right and one step to the left ftom the graphic. in order to show that it behaves as it if would be a continuation of the plot. At  , the deviation from the identitcal function becomes visible, and at
, the deviation from the identitcal function becomes visible, and at
 , the
, the  has many points with real values, including those with various negative integer values.
The tetration has cut at negative values of
has many points with real values, including those with various negative integer values.
The tetration has cut at negative values of  and singularities there. Therefore, the cuts of the modified tetration are determined by the lines
and singularities there. Therefore, the cuts of the modified tetration are determined by the lines  , and modified tetration unavoidable havs
singulatities in points
, and modified tetration unavoidable havs
singulatities in points  such that
such that  .
These singulatities are determined by the function
.
These singulatities are determined by the function  and do not depend on the base
and do not depend on the base  of tetration. In figure 11, the lines
of tetration. In figure 11, the lines  are seen not only along the real axis, but also at the top and at the bottom of the figure. In such a way, figure 11 shows the cutlines of the mofified tetration. One has no need to evaluate tetration in order to
see the margin of the hange of holomorphism of the modified tetration.
are seen not only along the real axis, but also at the top and at the bottom of the figure. In such a way, figure 11 shows the cutlines of the mofified tetration. One has no need to evaluate tetration in order to
see the margin of the hange of holomorphism of the modified tetration.
In fugure 12, the modified tetration is plotted in the coplex  -plane.
The additional cuts are seen in the upper and lower parts of the figure 12. Only within the strip along the real axis, the function is holomorphic. While the amplitude of sinusoidal is of order of
-plane.
The additional cuts are seen in the upper and lower parts of the figure 12. Only within the strip along the real axis, the function is holomorphic. While the amplitude of sinusoidal is of order of  , the strip of holomorphism is wider than unity, although this sidth slightly reduces along the real axis.
, the strip of holomorphism is wider than unity, although this sidth slightly reduces along the real axis.
In order to see the behavior of the modified tetration in vivinity of the additional singularities, in fig.13, the sooming-in of the part of figure 12 is shown.The zoom has improved resolution, so, in its turn, it can be zoomed in to the size of the screen of a computer to see the details. In each cell of the grid, the small and deformed image of the central part of the fig.12 appears.
One has no need to evaluate tetration in order to reveal its singulatities outside the real azis.
All the solutions  of equation
of equation  for integer
for integer  are singularities (branchpoints) of the modified tetration.
are singularities (branchpoints) of the modified tetration.
Let  .
.
The following theorem is suggested:
For any entire 1-periodic function  such that
such that
 ,
,  is not a constant,
is not a constant,
 ,
there exist
,
there exist  .
.
Although this theorem is not yet proved, the intents to construct at least one example of function, that woud contradict it, were not successful. This theorem is somehow independent from the theory of tetration, but it indicates, that any modified tetration cannot
be holomorphic in the range  .
.
Assording to the theorem above, the modified tetration does not satisfy the condition of quasi-periodicity, and does not satisfy the criterion of holomorphism in the definition of tetration. The sequance of cutlines for the epecific example of mofidied tetration is seen in figure 13; the modified tetration is not even continuous. An addition to function  smome highest sinusoidals brings the discontinuities even closer to the real axis. This indicates, that if in at least one point at the real axis between
smome highest sinusoidals brings the discontinuities even closer to the real axis. This indicates, that if in at least one point at the real axis between  and
and  , some solution
, some solution  of equations
of equations  ,
,  differs from tetration tet for at least
differs from tetration tet for at least  , then this solution is not holomorphic in the range
, then this solution is not holomorphic in the range  .
.
Even small deformation of tetration tet breaks its continuity. Similar reasons in favor of uniqueness tetration are suggested also in [1]. There is only one tetration, that satisfies requirements of the definition, although the rigorous mathematical proof of the uniqueness is still under development.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 D.Kouznetsov. Solutions of
 in the complex
in the complex  plane. Mathematics of Computation, 2008, in press; preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf Cite error: Invalid
plane. Mathematics of Computation, 2008, in press; preprint: http://www.ils.uec.ac.jp/~dima/PAPERS/analuxp99.pdf Cite error: Invalid <ref> tag; name "k" defined multiple times with different content Cite error: Invalid <ref> tag; name "k" defined multiple times with different content Cite error: Invalid <ref> tag; name "k" defined multiple times with different content
- ↑ 2.0 2.1 D.Kouznetsov. Ackermann functions of complex argument. Preprint of the Institute for Laser Science, UEC, 2008.
http://www.ils.uec.ac.jp/~dima/PAPERS/2008ackermann.pdf Cite error: Invalid
<ref> tag; name "k2" defined multiple times with different content
- ↑ R.L.Goodstein (1947). "Transfinite ordinals in recursive number theory". Journal of Symbolic Logic 12.
- ↑ 4.0 4.1
P.Walker. Infinitely differentiable generalized logarithmic and exponential functions. Mathematics
of computation, 196 (1991), 723-733.
- ↑
M.H.Hooshmand. ”Ultra power and ultra exponential functions”. Integral Transforms and
Special Functions 17 (8), 549-558 (2006)
- ↑ N.Bromer. Superexponentiation. Mathematics Magazine, 60 No. 3 (1987), 169-174
- ↑
W.Ackermann. ”Zum Hilbertschen Aufbau der reellen Zahlen”. Mathematische Annalen
99(1928), 118-133.
- ↑ 8.0 8.1 8.2
H.Kneser. “Reelle analytische L¨osungen der Gleichung
 und verwandter Funktionalgleichungen”.
Journal fur die reine und angewandte Mathematik, 187 (1950), 56-67. Cite error: Invalid
und verwandter Funktionalgleichungen”.
Journal fur die reine und angewandte Mathematik, 187 (1950), 56-67. Cite error: Invalid <ref> tag; name "kneser" defined multiple times with different content Cite error: Invalid <ref> tag; name "kneser" defined multiple times with different content





















































































































































































































































































































































