Reflection (geometry)

In analytic geometry, a reflection is a linear operation σ on a vector space with σ² = 1, i.e., σ is an involution. Reflecting twice an arbitrary vector brings back the original vector :

$\sigma ({\vec {\mathbf {r} }}\,)={\vec {\mathbf {r} }}\,'\quad {\hbox{and}}\quad \sigma ({\vec {\mathbf {r} }}\,'\,)={\vec {\mathbf {r} }}.$

PD Image
The vector $\scriptstyle {\vec {\mathbf {r} }}$ goes to $\scriptstyle {\vec {\mathbf {r} }}'$ under reflection in a plane. The unit vector $\scriptstyle {\hat {\mathbf {n} }}$ is normal to mirror plane.

Reflection in a plane

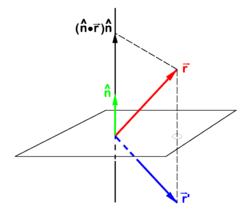
If ${\hat {\mathbf {n} }}$ is a unit vector normal (perpendicular) to a plane—the mirror plane—then $({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$ is the projection of ${\vec {\mathbf {r} }}$ on this unit vector. From the figure it is evident that

${\vec {\mathbf {r} }}-{\vec {\mathbf {r} }}\,'=2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }})\,{\hat {\mathbf {n} }}\;\Longrightarrow \;{\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$

If a non-unit normal ${\vec {\mathbf {n} }}$ is used then substitution of

${\hat {\mathbf {n} }}={\frac {\vec {\mathbf {n} }}{|{\vec {\mathbf {n} }}|}}\equiv {\frac {\vec {\mathbf {n} }}{n}}$

gives the mirror image,

${\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2{\frac {({\vec {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\vec {\mathbf {n} }}}{n^{2}}}$

This relation can be immediately generalized to m-dimensional inner product spaces. Let the space V_m allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,

$V_{m}=V_{1}\oplus V_{m-1}$

and let v be an element of the one-dimensional space V₁ then the involution

$r\mapsto r-2v{\frac {(v,r)}{(v,v)}}$

is a reflection of r in the hyperplane V_m−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.

Two consecutive reflections

PD Image
Fig. 2. Two reflections. Left: 3-dimensional drawing. Right: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect PQ in the point P′

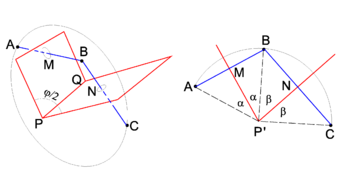
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection. The top drawing shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the lower drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle φ = 2α + 2β and the angle between the planes is α+β = φ/2.

From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an orthogonal matrix with determinant −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det(AB) = det(A)det(B), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation.