Tetration

Fig.1. Tetration $\mathrm {tet} _{b}(x)$ for $b=\mathrm {e}$, $b=2$, $b=\exp(1/\mathrm {e} )$, and $b={\sqrt {2}}$ versus $x$.

This article is currently under construction. While, use article from wikipedia http://en.wikipedia.org/wiki/Tetration

Tetration is fastly growing mathematical function, which was introduced in XX century and suggested for representation of huge numbers in mathematics of computation. However, up to year 2008, this function is not considered as elementary function, it is not implemented in programming languages and it is not used for the internal representation of data, at least in the commercial software.

Definiton

For real $b>1$, Tetration $F=\mathrm {tet} _{b}$ on the base $b$ is function of complex variable, which is holomorphic at least in the range $\{z\in \mathbb {C} :~\Re (z)>-2\}$, bounded in the range $\{z\in \mathbb {C} :~|\Re (z)|\leq 1\}$, and satisfies conditions

$F(z+1)=\exp _{b}\!{\big (}F(z){\big )}$

$F(0)=1$

$F\!{\big (}z^{*}{\big )}=F{\big (}z{\big )}^{*}$

at least within range $\Re (z)>-2$.

Etymology

Creation of word tetration is attributed to Englidh mathematician Reuben Louis Goodstein . This name indicates, that this operation is fourth (id est, tetra) in the hierarchy of operations after summation, multiplication, and exponentiation. In principle, one can define "pentation", "sexation", "septation" in the simlar manner, although tetration, perhaps, already has growth fast enough for the requests of XXI century.

Real values of the arguments

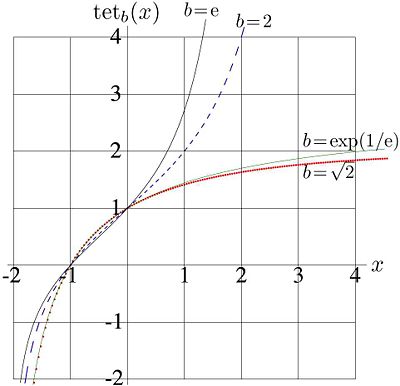
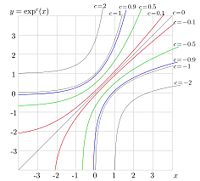
Examples of behavior of this function at the real axis are shown in figure 1 for values $b=\mathrm {e}$, $b=2$, $b=\exp(1/\mathrm {e} )$, and for $b={\sqrt {2}}$. It has logarithmic singularity at $-2$, and it is monotonously increasing function.

At $b\leq \exp(1/\mathrm {e} )$ tetration $\mathrm {tet} _{b}(x)$ approaches its limiting value as $x\rightarrow +\infty$, and $\displaystyle \lim _{x\rightarrow +\infty }~\mathrm {tet} _{b}(x)>1$.

Fast growth

At $b>\exp(1/\mathrm {e} )$ tetration $\mathrm {tet} _{b}(x)$ grows faster than any exponential function. For this reason the tetration is suggested for the representation of huge numbers in mathematics of computation. A number, that cannot be stored as floating point, could be represented as $\mathrm {tet} _{b}(x)$ for some standard value of $b$ (for example, $b=2$ or $b=\mathrm {e}$) and relatively moderate value of $x$. The analytic properties of tetration could be used for the implementation of arithmetic operations with huge numbers without to convert them to the floating point representation.

Integer values of the argument

For integer $z$, tetration ${\rm {tet}}_{b}$ can be interpreted as iterated exponential:

$\mathrm {tet} _{b}(1)=b$

$\mathrm {tet} _{b}(2)=b^{b}$

$\mathrm {tet} _{b}(3)=b^{b^{b}}$

and so on; then, the argument of tetration can be interpreted as number of exponentiations of unity. From definition it follows, that

$\mathrm {tet} _{b}(0)=1$

and

$\mathrm {tet} _{b}(-\!1)=0$

Relation with the Ackermann function

At base $b=2$, tetration is related to the Ackermann function:

$\mathrm {tet} _{2}(n+3)=A(4,n)+3$

where Ackermann function $A$ is defined for the non-negative integer values of its arguments with equations

$A(m,n)=\left\{{\begin{array}{llll}n+1&,&{\rm {if~}}~m\!=\!0\\A{\big (}m\!-\!1,~1~{\big )}&,&{\rm {if~}}m\!>\!0{\mbox{ and }}n\!=\!0\\A{\Big (}m\!-\!1,A(m,n\!-\!1){\Big )}&,&{\rm {if~}}m\!>\!0{\mbox{ and }}n\!>\!0\end{array}}\right.$

Asymptotic behavior of tetration

The analytic extension of tetration $~F(z)$ grows fast along the real axis of the complex $z$-plane, at least for some values of base $b$. However, it cannot grow infinitely in the direction of imaginary axis. The exponential convergence of discrete interation of logarithm corresponds to the exponential asymptotic behavior

(12) $F(z)=L+\varepsilon (z)+o{\big (}\varepsilon (z)^{2}{\big )}$

where

(13) $\varepsilon (z)=\exp(Qz+r)$,

$Q$ and $r$ are fixed complex numbers, and $L$ is eigenvalue of logarithm, solution of equation

(14) $x=\log _{b}(x)$.

FIg.2. Graphic solution of equation $x=\log _{b}(x)$ for $b={\sqrt {2}}$ (two real solutions, $x=2$ and $x=4$), $b=\exp(1/{\rm {e)}}$ (one real solution $x={\rm {e}}$) $b=2$ (no real solutions).

Solutions of equation (14) are called fixed points of logarithm.

Fixed points of logarithm

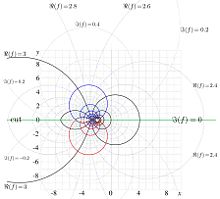
Three examples of graphical solution of equation (14) are shown in figure 2 for $b={\sqrt {2}}$, $b=\exp(1/{\rm {e)}}$, and $b=2$.

The black line shows function $y=x$ in the $x,y$ plane. The colored curves show function $y=\log _{b}(x)$ for cases $b={\sqrt {2}}$ (red), $b=\exp(1/{\rm {e)}}$ (green), and $b=2$ (blue).

At $b={\sqrt {2}}$, there exist 2 solutions, $x=2$ and $x=4$.

At $b=\exp(1/{\rm {e)}}$ there exist one solution $x={\rm {e}}$.

and $b=2$, there are no real solutions.

In general,

• at $b<\exp(1/{\rm {e)}}$ there are two real solutions
• at $b=\exp(1/{\rm {e)}}$, there is one soluition, and
• at $b>\exp(1/{\rm {e)}}$ there esist two solutions, but they are complex.

In particular, at $b={\sqrt {2}}$, the solutions are
$x=L_{{\sqrt {2}},1}=2$ and $x=L_{{\sqrt {2}},2}=4$
.

At $b=2$, the solutions are
$x=L_{2}\approx 0.824678546142074222314065+1.56743212384964786105857\!~{\rm {i}}$ and
$x=L_{2}^{*}\approx 0.824678546142074222314065-1.56743212384964786105857\!~{\rm {i}}$.

At $b={\rm {e}}$, the solutions are
$x=L_{\rm {e}}\approx 0.318131505204764135312654+1.33723570143068940890116\!~{\rm {i}}$ and
$x=L_{\rm {e}}^{*}\approx 0.318131505204764135312654-1.33723570143068940890116\!~{\rm {i}}$.

Few hundred straightforward iterations of equation (14) are sufficient to get the error smaller than the last decimal digit in the approximations above.

FIg.3. parameters of asymptotic of tetration versus logarithm of the base

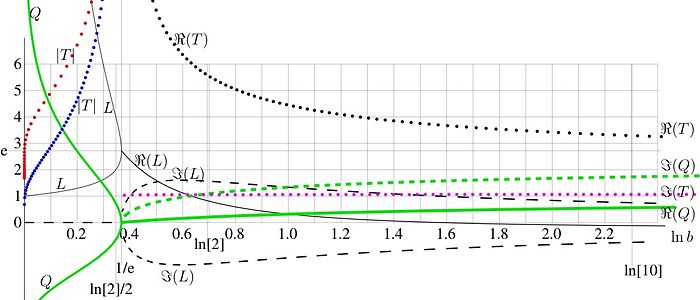
The solutions $x=L_{1}$ and $x=L_{2}$ of equation (14) are plotted in figure 3 versus $\beta =\ln(b)$ with thin black lines. Let $L_{1}<L_{2}$, and only at $\ln(b)=1/e$, the equality $L_{1}=L_{2}$ takes place. Basic properties of tetration are determined by the base $b$. The main parameters versus $\ln(b)$ are plotted in figure 3. The thin black solid curve at $\beta \geq 1/{\rm {e}}$ represents the real part of the solutions $L$ and $L^{*}$ of (14); the thin black dashed curve represents the two options for the imaginary part; the two solutions are complex conjugaitons of each other. Requirement of definition of tetration determine the asymptotic of the solution. Parameter $Q$ tetermines periodicity of quasi-periodicity of tetration. The two solutions for <\math>Q</math>are shown in figure 3 with green lines.

At $b<\exp(1/\mathrm {e} )$ both solutons for <\math>Q</math> are real. The negative $Q$ corresponds to tetration, decaying to the asymptotic value $L$ in the direction of real axis; positive </math>Q</math> corresponds to the solution growing along the real axis. At the real axix, such a solution remains larger than unity; this does not allow to satisfy confition $F(0)=1$. Therefore, only one negative $Q$ corresponds to the asymptotic behavior of tetration.

At $b>\exp(1/\mathrm {e} )$, both options for $Q$ are mutually complex conjugate. The real part is shown thif thick green line; one option of the imaginary part is shown with dashed line.

Possibilities for the period (or quasi-period) $T={\frac {2\pi }{Q}}$ are shown in Figure 3 with fotted lines. At $b>\exp(1/\mathrm {e} )$, only "negative" period forresponds to tetration. At $b>\exp(1/\mathrm {e} )$, the periodicity can be achieved only asymptotically; and $T$ is quasi-period. The real part of quasi-period is markes with black dotted line; one of two options tor the imaginary part is marked with pink dotted line.

Generally, at $1<b<\exp(1/\mathrm {e} )$, tetration is periodic; the period is pure imaginary.

At $b=\exp(1/\mathrm {e} )$, tetration is not periodic, and no exponential asymptotic exist.

$b>\exp(1/\mathrm {e} )$, tetration is quasi–periodic, the quasi-period in the upper complex half-plane is conjugate to that in the lower complex half-plane. The larger is base $b$, the shorter is quasi-period. As the quasi-periods are complex conjugated, the quasi-periodicity takes place away from the real axis.

Evaluation of tetration

Fig.4. Tetration $f=F(z)$ at the complex $z$-plane. .

As the asymptoric of tetration is crutually depend of base $b$ in ficinity of value $b=\exp(1/\mathrm {e} )$, the evaluation procidure is different foe the cases $1<b<\exp(1/\mathrm {e} )$, $b=\exp(1/\mathrm {e} )$, and $b>\exp(1/\mathrm {e} )$, and should be considered intependently.

Case $1<b<\exp(1/\mathrm {e} )$

At $1<b<\exp(1/\mathrm {e} )$, the period $T$ is imaginary. Period with smallest modulus corresponds to the solution that is unity at the origen of coordinates. For $b={\sqrt {2}}$, function $f=\mathrm {tet} _{b}(z)$ is shown in figure 4 with levels of constant real part and levels of constant imaginary part. Levels $\Re (f)=2,3,4$ and levels $\Im (f)=0,\pm 1,\pm 2\pm 3,\pm 4$ aew shown with thick lines. Intermediate levels are shown with thin lines. There are branch points at $\Re (z)=2~,~\Im (z)=2\pi |T|m~\forall m\in \mathbb {N}$; the cut lines are $\Re (z)<2~,~\Im (z)=2\pi |T|m~\forall m\in \mathbb {N}$. For this value of base, the period

Failed to parse (syntax error): {\displaystyle T=\frac{2\pi}{\ln^2(2)}\approx −17.1431481793548471041794 ~\mathrm{i}} .

The solution follows asymptotic at large values of real part of the argument, exponentially approaching the limiting value. In particular, for $b={\sqrt {2}}$, this limiting value is 2.

The trace of the solution along the real axis corresponds to the red dotted curve in Figure 1. Other solution of the recursive equaiton () do not satisfy criteria formulated in the definition of tetration.

Case $b=\exp(1/\mathrm {e} )$

(CC) Image: Dmitrii Kouznetsov
Fig.5. Tetration at $b=\exp(1/\mathrm {e} )$.

At $b=\exp(1/\mathrm {e} )$, asymptotically

$F(z)=\mathrm {e} -2\mathrm {e} /z+{\mathcal {O}}(1/z^{2})$

The function $f=F(x+\mathrm {i} y)$ is shown in figure 5.

Levels $\Re (f)=-2,-1,0,1,2,3,4$ are shown with thick black lines.

Levels $\Im (f)=-1,-2,-3,-4$ are shown with thick red lines.

Levels $\Im (f)=1,2,3,4$ are shown with thick blue lines.

Intermediate levels are shown with thin lines.

There is cut at $x<-2$, $y=0$.

Behavior of this function at real values of argument is shown in Figure 1 with thin solid line.

Case $b>\exp(1/\mathrm {e} )$

(CC) Image: Dmitrii Kouznetsov
Fig.6. Tetration $\mathrm {tet} _{b}(x+\mathrm {i} y)$at base $b=2$ and $b=\mathrm {e}$.

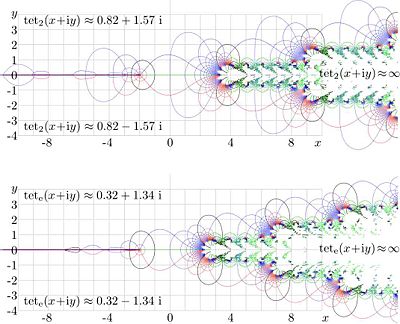
At $b>\exp(1/\mathrm {e} )$, tetration is asymptotically periodic. It exponentially decays to the fixed points $L$ and $L^{*}$ in th eupper and lower halfplane. This allows to express it through its values along the imaginary axis, using the Cauchi integral. .

For the base $b=2$ and $b=\mathrm {e}$ tetration $f=\mathrm {tet} _{b}(z)$ is plotted in figure 6. Levels $\Re {f}=0,\pm 1,...\pm 16$ and $\Im {f}=0,\pm 1,...\pm 16$ are drawn with thick lines. The function has logarithmic singulatiry at point -2 and cut at real values of the argument, smaller than -2. In the right hand side, symbols $\approx \infty$ mean huge values that cannot be stored in the conventional floating point representation (logarithm, mantissa). In the upper left and lower left part of eath graphic, the function approaches its asymptotic values $L$ and $L^{*}$. Function is quasi-periodic; the same fractal structure reproduces again and again at the translation of argument with quasiperiod $T$ in the upper halfplane and $T^{*}$ in the lower halfplane.

Along the real axis, tetration for this values of base is plotted also in figure 1 with thick solid and dashed lines.

Inverse of tetration

(CC) Image: Dmitrii Kouznetsov
Fig.7. kslog in the complex plane.

The inverse of tetration $t=\mathrm {kslog} (z)=\mathrm {tet} ^{-1}(z)$ can be performed using the Newton method, solving equation $\mathrm {tet} (t)=z$, leading to

$\mathrm {tet} {\big (}\mathrm {kslog} (z){\big )}=z$.

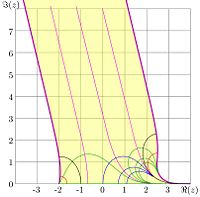
The inverse function has branchpints $L$ and $L^{*}$. For the kslog, at base $b=\mathrm {e}$, shown in the figure 7, the cuts are placed horisontaly, along the lines

$\Re (z)<\Re (L)$, $\Im (z)=\pm \Im (L)$.

Due to the symmetry $\mathrm {kslog} {\big (}z^{*}{\big )}=\mathrm {kslog} {\big (}z{\big )}^{*}$, it is sufficient to plot only half of the complex plane.

(CC) Image: Dmitrii Kouznetsov
Fig.8. Shaded region is image of the upper halfplane at the mapping with kslog function.

The mapping with function kslog is shown in figure 8. For $x$ in the shaded region, the relation

$\mathrm {kslog} {\big (}\mathrm {tet} (z){\big )}=z$

takes place. The upper part of the complex plane is mapped into the upper halfplane, and the lower halfplane is mapped to the lower halfplane. The real axis is mapped into the halfline $(-2,\infty )$. The fixed points $L$ is mapped to imaginary infinity, following the shadower strip.

In figure 8, the images of the grid lines $\Re (z)=-1,0,\Re (L),1,2,3$ and images of the grid lines $\Im (z)=1,\Im (L),2,3,4$ are shown. These curves reproduce levels $\Re (F(z))={\rm {const}}$ and $\Im (F(z))={\rm {const}}$ shown in figure 6 for $b={\rm {e}}$.

Together, the pair of functions tet and kslog allow to evaluate any iteration (including negative, fractional and even complex) of the exponential finction.

Iterated exponential and ${\sqrt {\exp }}$

Fig.9. $\exp ^{c}(z)$ in the complex $z$ plane for various $c$.

Fig.10. $\exp ^{c}(x)$ versus $x$

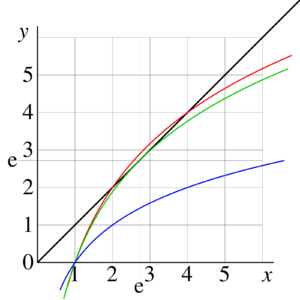
Holomorphic tetration allows to extend the iterated exponential $\exp _{b}^{c}$

$\exp _{b}^{0}(z)=z$

$\exp _{b}^{1}(z)=\exp _{b}(z)$

$\exp _{b}^{2}(z)=\exp _{b}\!{\Big (}\exp _{b}(z){\Big )}$

$\exp _{b}^{c+1}(z)=\exp _{b}\!{\Big (}\exp _{b}^{c}(z){\Big )}$

For non-integer values of $c$. It can be defined as

$\exp _{b}^{c}(z)=\mathrm {tet} _{b}\!{\Big (}c+{\mathrm {tet} _{b}}^{-1}(z){\Big )}$

If in the notation $\exp _{b}^{c}$ the superscript is omitted, it is assumed to be unity; for example $\exp _{b}^{1}=\exp _{b}$. If the subscript is omitted, it is assumed to be $\mathrm {e}$, id est, $\exp ^{c}=\exp _{\mathrm {e} }^{c}$

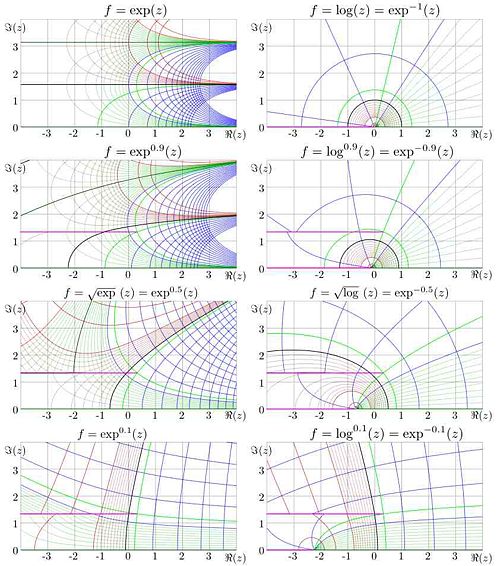
Function $f=\exp ^{c}(z)$ is shown in figure 9 with levels of constant real part and levels of constant imaginary part. Levels $\Re (f)=-3,-2,-1,0,1,2,3,4,5,6,7,8,9$ and $\Im (f)=-3,..14$ are drown with thick lines. Red corresponds to a negative value of the real or the imaginaryt part, black corresponds to zero, and blue corresponds to the positeive values. Levels $\Re (f)=-0.2,-0.4,-0.6,-0.8$ are shown with thin red lines. Levels $\Im (f)=0.2,0.4,0.6,0.8$ are shown with thin green lines. Levels $\Re (f)=\Re (L)$ and Levels $\Im (f)=\Im (L)$ are marked with thick green lines, where $L\approx 0.31813150520476413+1.3372357014306895~\mathrm {i}$ is fixed point of logarithm. At non-integer values of $c$, $L$ and $L^{*}$ are branch points of function $\exp ^{c}$; in figure, the cut is placed parallel to the real axis. At $c<0$ there is an additional cut which goes along the negative part of the real axis. In the figure, the cuts are marked with pink lines.

For real values of the argument, function $y=\exp ^{c}(x)$ is ploted in figure 10 versus $x$ for values $c=0,\pm 0.1,\pm 0.5,\pm 0.9,\pm 1,\pm 2$.
in programming languages, inverse function of exp is called log.

For logarithm on base e, notation ln is also used. In particular, $\exp ^{-1}(x)=\ln(x)$, $\exp ^{-2}(x)=\ln {\big (}\ln(x){\big )}$ and so on.

Free online sources

• http://reglos.de/lars/ffx.html , Lars Kindermann. References about Iterative Roots and Fractional Iteration.
• http://math.eretrandre.org/tetrationforum/index.php , Discussion about tetration
• http://tetration.itgo.com/ Tetration site by Andrew Robbins
• http://www.tetration.org/ Tetration site by Daniel Geisler