Platonic solid
The platonic solids (named after the Greek philosopher Plato) are a family of five convex polyhedra which exhibit a particularly high symmetry. They can be characterized by the following two properties: All its sides (faces) are regular polygons and congruent to each other, and the same number of sides meet in all its corners (vertices). However, they also satisfy the following much stronger symmetry condition: Each flag, i.e. each sequence consisting of a corner of an edge of a face, "looks the same". i.e., cannot be distinguished from the others by its position on the polyhedron. Because of this latter property they are called regular polyhedra.
The Greek names of the platonic solids are derived from the number of sides:
- Tetrahedron: 4 equilateral triangles, 4 corners in which 3 sides meet
- Hexahedron (or cube): 6 squares, 8 corners in which 3 sides meet
- Octahedron: 8 equilateral triangles, 6 corners in which 4 sides meet
- Dodecahedron: 12 regular pentagons, 20 corners in which 3 sides meet
- Icosahedron: 20 equilateral triangles, 12 corners in which 5 sides meet
| number of faces |
name | type of face | volume | surface area |
properties | image |
|---|---|---|---|---|---|---|
| 4 | regular tetrahedron (or regular triangular pyramid) |
equilateral triangle | 4 vertices, 6 edges, self-dual | 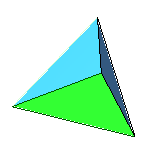
| ||
| 6 | cube | square | 8 vertices, 12 edges, dual to octahedron | 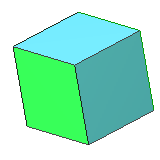
| ||
| 8 | regular octahedron | equilateral triangle | 6 vertices, 12 edges, dual to cube | 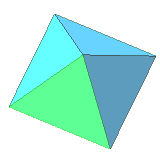
| ||
| 12 | regular dodecahedron | regular pentagon | 20 vertices, 30 edges, dual to icosahedron | 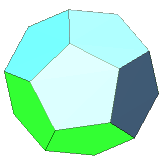
| ||
| 20 | regular icosahedron | equilateral triangle | 12 vertices, 30 edges, dual to dodecahedron | 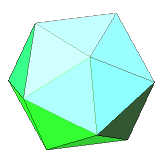
|
The dual of a polyhedron is the polyhedron formed by taking the center of each face as the vertex of the dual. The regular tetrahedron is self-dual - connecting the center of each face results in a smaller tetrahedron. The cube and regular octahedron are dual to each other, and the regular dodecahedron and icosahedron are dual to each other.
A sphere circumscribed about any of the Platonic solids will touch all the vertices, and a sphere inscribed within any will touch all the faces at the center of the face.
Proof that there are only 5 Platonic solids
Proving that there are at most 5 Platonic solids is rather easy: From the definition, the faces must be regular polygons which can meet three or more at a point with some excess angle, to create a solid angle. Any regular polygon with 7 or more sides cannot meet three or more to a point without overlapping. The regular hexagon can meet three at a point, but with no excess, thus no solid angle is formed. That leaves the regular pentagon, the square, and the equilateral triangle as the only possible faces for a Platonic solid. The regular pentagon and the square can only meet three at a point and have any excess to allow forming a solid angle. The Platonic solids thus formed are the dodecahedron and the cube. The equilateral triangle can meet three, four, or five at a point and form a solid angle; the figures formed are the tetrahedron, octahedron, and icosahedron, respectively.









