Revision as of 02:10, 29 October 2008 by imported>Dmitrii Kouznetsov
Exponential function or exp, can be defined as solution of differential equaiton

with additional condition

Exponential function is believed to be invented by Leonarf Euler some centuries ago.
Since that time, it is widely used in technology and science; in particular, the exponential growth
is described with such function.
Properties
exp is entire function.
For any comples  and
and  , the basic property holds:
, the basic property holds:

The definition allows to calculate all the derrivatives at zero; so, the Tailor expansion has form

where  means the set of complex numbers.
The series converges for and complex
means the set of complex numbers.
The series converges for and complex  . In particular, the series converge for any real value of the argument.
. In particular, the series converge for any real value of the argument.
Inverse function
Inverse function of the exponential is logarithm; for any complex  , the relation holds:
, the relation holds:

Exponential also can be considered as inverse of logarithm, while the imaginary part of the argument is smaller than  :
:

While lofarithm has cut at the negative part of the real axis, exp can be considered
Number e
 is widely used in applications; this notation is commonly accepted. Its approximate value is
is widely used in applications; this notation is commonly accepted. Its approximate value is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm e}=\exp(1) \approx 2.71828 18284 59045 23536}
Relation with sin and cos functions

Generalization of exponential
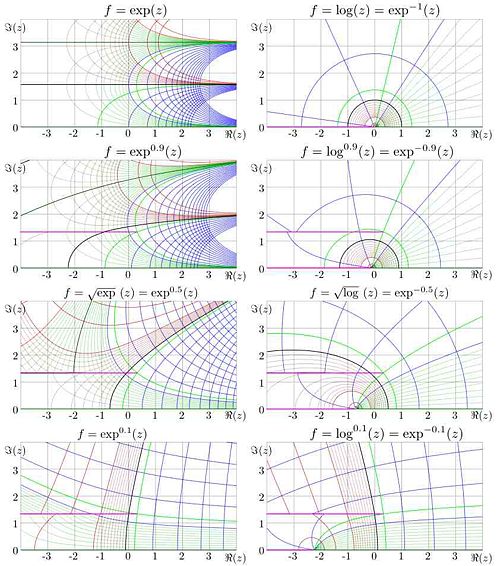

in the complex

plane for some real values of

.
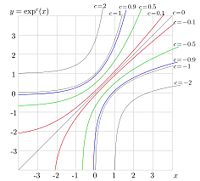

versus

for some real values of

.
Notation  is used for the exponential with scaled argument;
is used for the exponential with scaled argument;

Notation  is used for the iterated exponential:
is used for the iterated exponential:




For non-integer values of  , the iterated exponential can be defined as
, the iterated exponential can be defined as

where  is function
is function  satisfying conditions
satisfying conditions



The inverse function is defined with condition

and, within some range of values of 

If in the notation  superscript is omitted, it is assumed to be unity; for example
superscript is omitted, it is assumed to be unity; for example
 . If the lower superscript is omitter, it is assumed to be
. If the lower superscript is omitter, it is assumed to be  , id est,
, id est,

References
- Ahlfors, Lars V. (1953). Complex analysis. McGraw-Hill Book Company, Inc..
- H.Kneser. ``Reelle analytische L\"osungen der Gleichung

und verwandter Funktionalgleichungen. Journal f\"ur die reine und angewandte Mathematik, 187 (1950), 56-67.






































