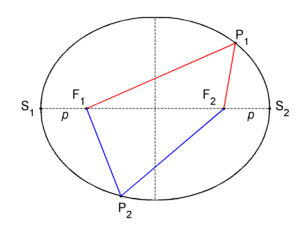
PD Image Fig. 1. Ellipse (black closed curve). The sum of the lengths of the two red line segments (ending in P
1) is equal to the sum of the lengths of the two blue line segments (ending in P
2).
In mathematics, an ellipse is a planar locus of points characterized by having an equal sum of distances to two given fixed points in the plane. In figure 1 two fixed points F1 and F2 are shown, these are the foci of the ellipse. An arbitrary point P1 on the ellipse has distance |F1P1| to F1 and distance |F2P1| to F2. Let d be the sum of distances of P1 to the foci,

then all points of the ellipse have the sum of distances d. Thus,
another arbitrary point P2 on the ellipse has distance |F1P2| to F1 and distance |F2P2| to F2. By definition the sum of distances of P2 to the foci is equal to d,

The horizontal line segment S1–S2 in figure 1, going through the foci, is known as the major axis of the ellipse. Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway the foci perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and minor axes are distinguished by a ≥ b. When a = b the ellipse is a circle—a special case of an ellipse. Clearly both axes are symmetry axes, reflection in either of them transforms the ellipse into itself. Basically, this a consequence of the fact that a reflection conserves (sums of) distances. The intersection of the axes is the center of the ellipse.
The two foci and the points S1 and S2 are connected by reflection in the minor axis. Hence the distance |S2F2| ≡ p is by symmetry equal to the distance |S1F1|. The distance of S2 to F1 is equal to 2a − p. The distance of S2 to F2 is equal to p. By the definition of the ellipse the sum is equal to d, hence

The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis.
Eccentricity
The eccentricity e of an ellipse (usually denoted by e or ε) is the ratio of the distance |OF2| ( (cf. figure 2) to half the length a of the major axis, that is, e ≡ |OF2|/a. Let  be a vector of length a along the x-axis, then
be a vector of length a along the x-axis, then

The following two vectors have common endpoint at P, see figure 2,

Move P now to the positive y-axis; its new position vector is:

By symmetry, the distance of the moved P to either focus is equal to half the length of the major axis (a) and equal to the length of the new vector  (with endpoint on the y-axis). For the following two inner products (indicated by a centered dot) we find,
(with endpoint on the y-axis). For the following two inner products (indicated by a centered dot) we find,

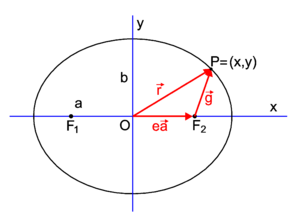
PD Image Fig. 2. An ellipse situated such that the major and minor axis are along
Cartesian axes. The center of the ellipse coincides with the origin O.
Hence, (in fact by the Pythagoras theorem applicable for P on the y-axis),

so that the eccentricity is given by

Algebraic form
For a point P=(x,y) on an ellipse that is located with respect to a Cartesian frame as in figure 2, it holds that

Note that this equation is reminiscent of the equation for a unit circle. An ellipse may be seen as a unit circle in which the x and the y coordinates are scaled independently, by 1/a and 1/b, respectively.
Proof
Introduce the vectors

By definition of ellipse, the sum of the lengths is 2a

Multiply Eq. (1) by

and work out the left-hand side:

Hence

Use

and one obtains

Add and subtract Eqs (1) and (2) and we find expressions for the distance of P to the foci,

Square both equations

Adding, using the earlier derived value for e2, and reworking gives

Division by b2 gives finally

Polar representation relative to focus
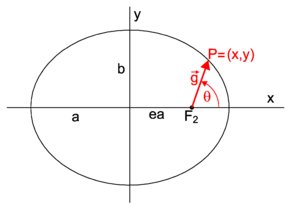
PD Image Fig. 3. Polar representation
The length g of the vector (cf. figure 3)

is given by the polar equation

where ℓ is known as the semi-lactus rectum of the ellipse.
Proof
Earlier [Eq. (3)] it was derived for the distance from the right focus F2 to P that

Elimination of x from

gives

so that

Substitute

and the polar equation for the ellipse follows.































